Rachunek prawdopodobieństwa MAP1064

Wydział Elektroniki, rok akad. 2008/09, sem. letni

Wykładowca: dr hab. A. Jurlewicz

Przykłady do listy 1: Całki podwójne

Przykłady do zadania 1.1 :
Obliczyć dane całki podwójne po wskazanych prostokątach

(a)

Z Z

R

sin(x + y) dxdy, R =

−

π

4

,

π

4

×

0,

π

4

•

Z Z

R

sin(x + y) dxdy =

π

4

Z

−

π

4

dx

π

4

Z

0

sin(x + y)dy =

• =

π

4

Z

−

π

4

(− cos(x + y)

y=

π

4

y=0

dx =

π

4

Z

−

π

4

(− cos(x +

π

4

) + cos x)dx =

• = (− sin(x +

π

4

) + sin x

x=

π

4

x=−

π

4

= − sin

π

2

+ sin

π

4

+ sin 0 − sin

−

π

4

=

√

2 − 1

(b)

Z Z

R

(x

2

+ y

2

x) dxdy, R = [−1, 1] × [2, 4]

•

Z Z

R

(x

2

+ y

2

x) dxdy =

4

Z

2

dy

1

Z

−1

(x

2

+ y

2

x)dx =

• =

4

Z

2

x

3

3

+ y

2

·

x

2

2

x=1

x=−1

dy =

4

Z

2

2

3

+ 0

dy =

• =

2

3

· 2 =

4

3

(c)

Z Z

R

e

x+y

dxdy, R = [0, 1] × [0, 1]

•

Z Z

R

e

x+y

dxdy =

Z Z

R

e

x

e

y

dxdy =

• =





1

Z

0

e

x

dx





·





1

Z

0

e

y

dy





=





1

Z

0

e

x

dx





2

=

• =





e

x

x=1

x=0





2

= (e − 1)

2

(d)

Z Z

R

xy(x + y) dxdy, R = [−1, 1] × [−1, 1]

•

Z Z

R

xy(x + y) dxdy =

Z Z

R

x

2

y dxdy +

Z Z

R

xy

2

dxdy =

• =





1

Z

−1

x

2

dx





·





1

Z

−1

ydy





+





1

Z

−1

xdx





·





1

Z

−1

y

2

dy





= 2





1

Z

−1

x

2

dx





·





1

Z

−1

ydy





= 0,

bo druga całka w iloczynie równa jest 0 jako całka z funkcji nieparzystej po przedziale
symetrycznym względem 0.

1

Przykłady do zadania 1.2 :
Podane całki podwójne zamienić na całki iterowane i obliczyć. Narysować obszar całkowania.

(a)

Z Z

D

1

(1 + x + y)

2

dxdy, gdzie D =

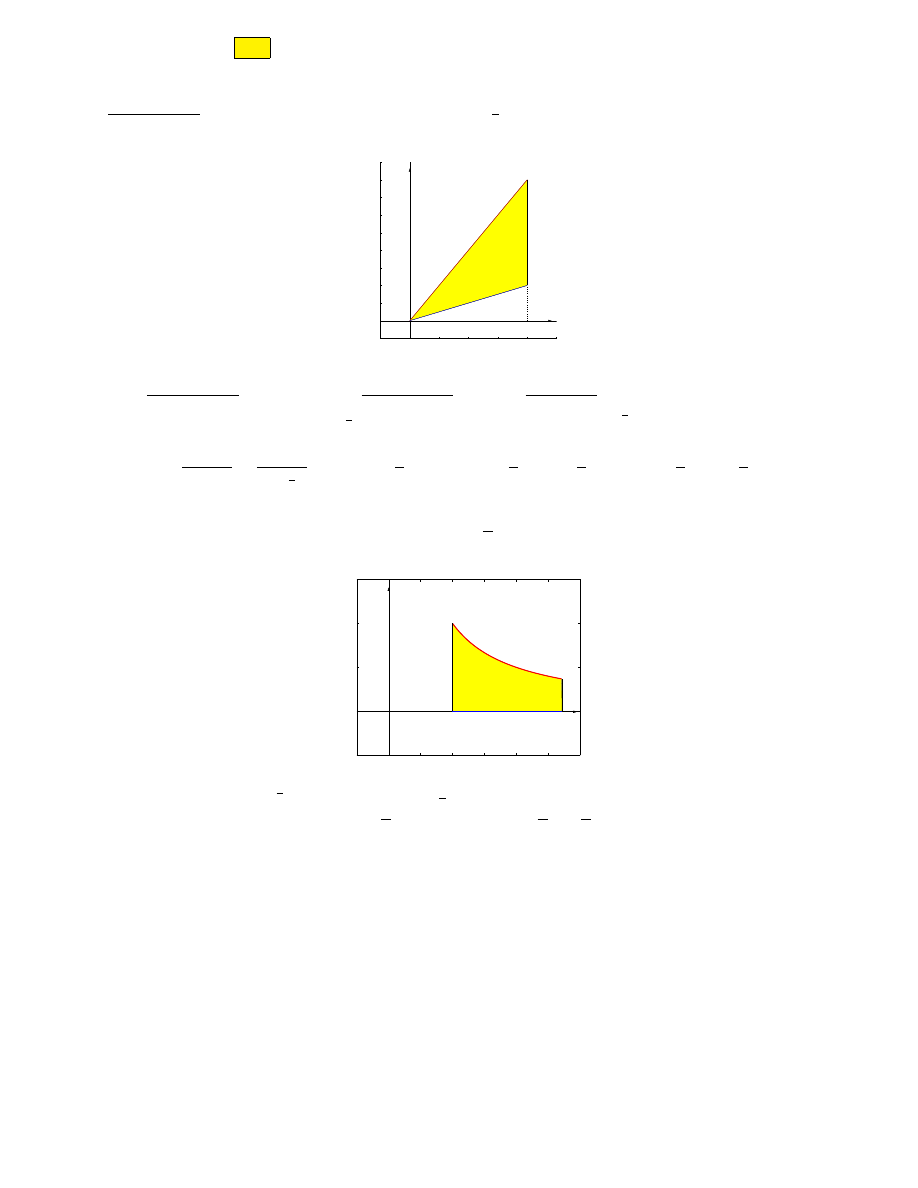
n

(x, y) : 0 ¬ x ¬ 2,

x
2

¬ y ¬ 2x

o

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

y

x

2

0

y=2x

y=x/2

•

Z Z

D

1

(1 + x + y)

2

dxdy =

2

Z

0

dx

2x

Z

x
2

dy

(1 + x + y)

2

=

2

Z

0





−

1

1 + x + y

y=2x

y=

x
2





dx =

=

2

Z

0

−

1

1 + 3x

+

1

1 +

3
2

x

!

dx =





−

1

3

ln |1 + 3x| +

2

3

ln

1 +

3

2

x

x=2

x=0

= −

1

3

ln 7 +

2

3

ln 4

(b)

Z Z

D

e

xy

dxdy, gdzie D =

(x, y) : 1 ¬ x ¬ e, 0 ¬ y ¬

1

x

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

3

−0.5

0

0.5

1

1.5

y

x

1

e

y=1/x

y=0

•

Z Z

D

e

xy

dxdy =

e

Z

1

dx

1
x

Z

0

e

xy

dy =

e

Z

1





1

x

e

xy

y=

1
x

y=0





dx =

e

Z

1

1

x

e −

1

x

dx =

=

(e − 1) ln |x|

x=e

x=1

= e − 1

2

(c)

Z Z

D

x dxdy, gdzie D =

n

(x, y) : 0 ¬ x ¬ 1, 0 ¬ y ¬

√

1 − x

2

o

.

• rysunek

−0.5

0

0.5

1

1.5

−0.5

0

0.5

1

1.5

y

x

1

0

y=(1−x

2

)

1/2

•

Z Z

D

x dxdy =

1

Z

0

dx

√

1−x

2

Z

0

xdy =

1

Z

0





xy

y=

√

1−x

2

y=0





dx =

1

Z

0

x

√

1 − x

2

dx =








y = 1 − x

2

dy = −2xdx

x 0 1

y 1 0








=

= −

1

2

0

Z

1

√

ydy =





−

1

2

·

y

3/2

3/2

y=0

y=1

=

1

3

Przykłady do zadania 1.3 :

Obszar D ograniczony jest krzywymi o podanych równaniach. Całke podwójną

Z Z

D

f (x, y) dxdy

(gdzie f (x, y) jest ciągła na D) zamienić na dwa rodzaje całek iterowanych.

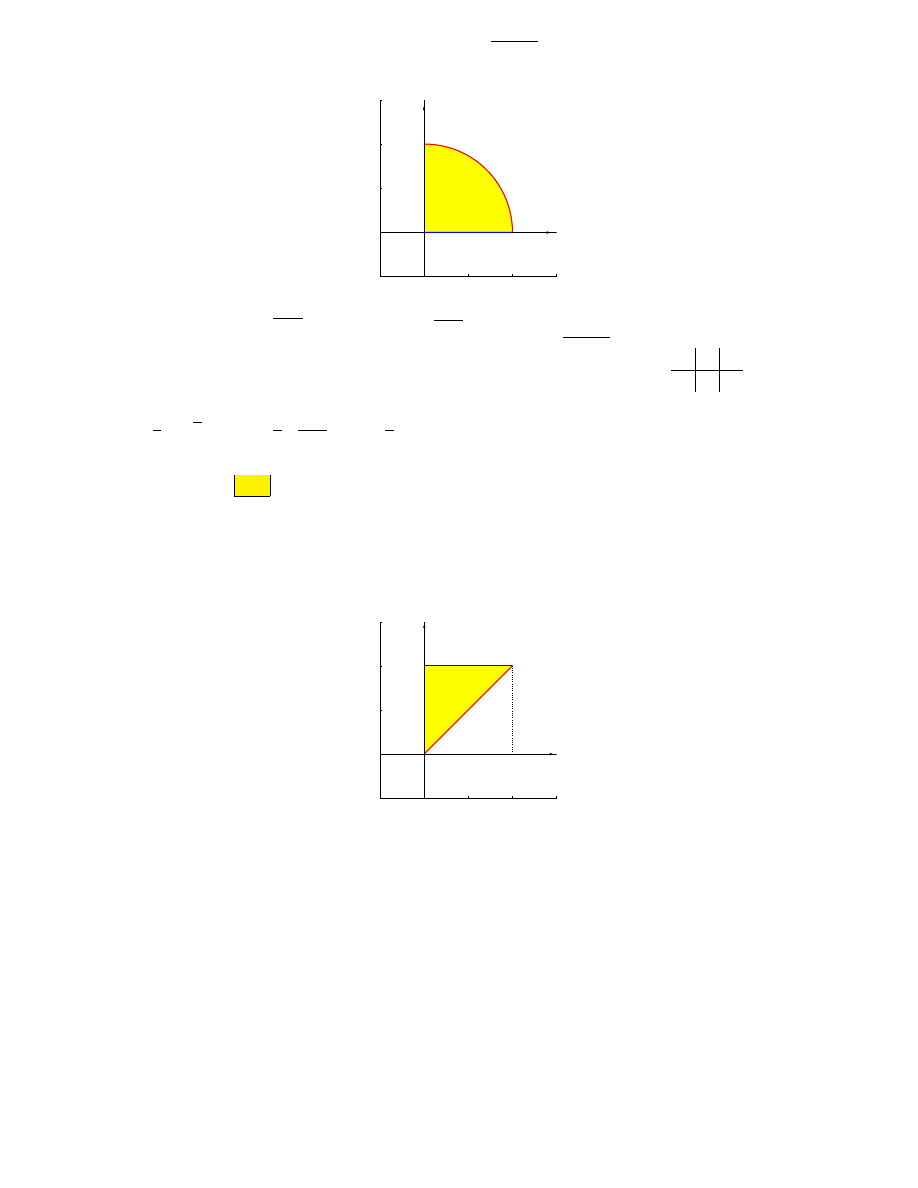
(a) x = 0, y = 1, y = x

• rysunek

−0.5

0

0.5

1

1.5

−0.5

0

0.5

1

1.5

y=1

x=0

y=x

1

1

0

x

y

• D to obszar normalny względem osi 0x, bo

D = {(x, y) : 0 ¬ x ¬ 1, x ¬ y ¬ 1}

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

0

dx

1

Z

x

f (x, y)dy

• D to także obszar normalny względem osi 0y, bo

D = {(x, y) : 0 ¬ y ¬ 1, 0 ¬ x ¬ y}

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

0

dy

y

Z

0

f (x, y)dx

3

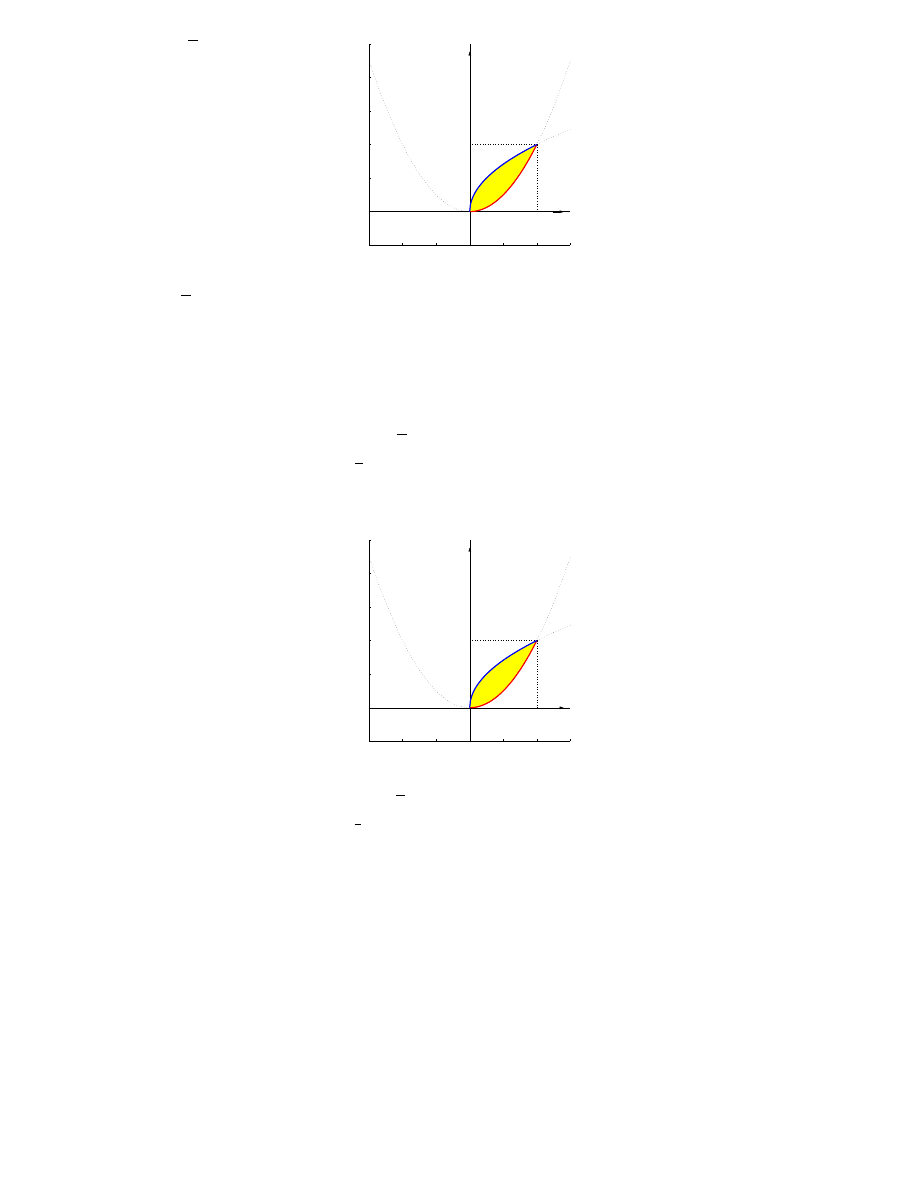
(b) y = x

2

, y =

√

x

• rysunek

−1.5

−1

−0.5

0

0.5

1

1.5

−0.5

0

0.5

1

1.5

2

2.5

y

x

1

1

0

y=x

2

y=x

1/2

• szukamy punktów wspólnych podanych krzywych:

x

2

=

√

x

x

4

= x, x ­ 0

x(x

3

− 1) = 0, x ­ 0

x = 0 ∨ x = 1

,

dla x = 0 mamy y = 0

2

= 0, dla x = 1 mamy y = 1

2

= 1

• D to obszar normalny względem osi 0x, bo

D = {(x, y) : 0 ¬ x ¬ 1, x

2

¬ y ¬

√

x}

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

0

dx

√

x

Z

x

2

f (x, y)dy

• rysunek

−1.5

−1

−0.5

0

0.5

1

1.5

−0.5

0

0.5

1

1.5

2

2.5

y

x

1

1

0

x=y

1/2

x=y

2

• D to także obszar normalny względem osi 0y, bo

D = {(x, y) : 0 ¬ y ¬ 1, y

2

¬ x ¬

√

y}

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

0

dy

√

y

Z

y

2

f (x, y)dx

4

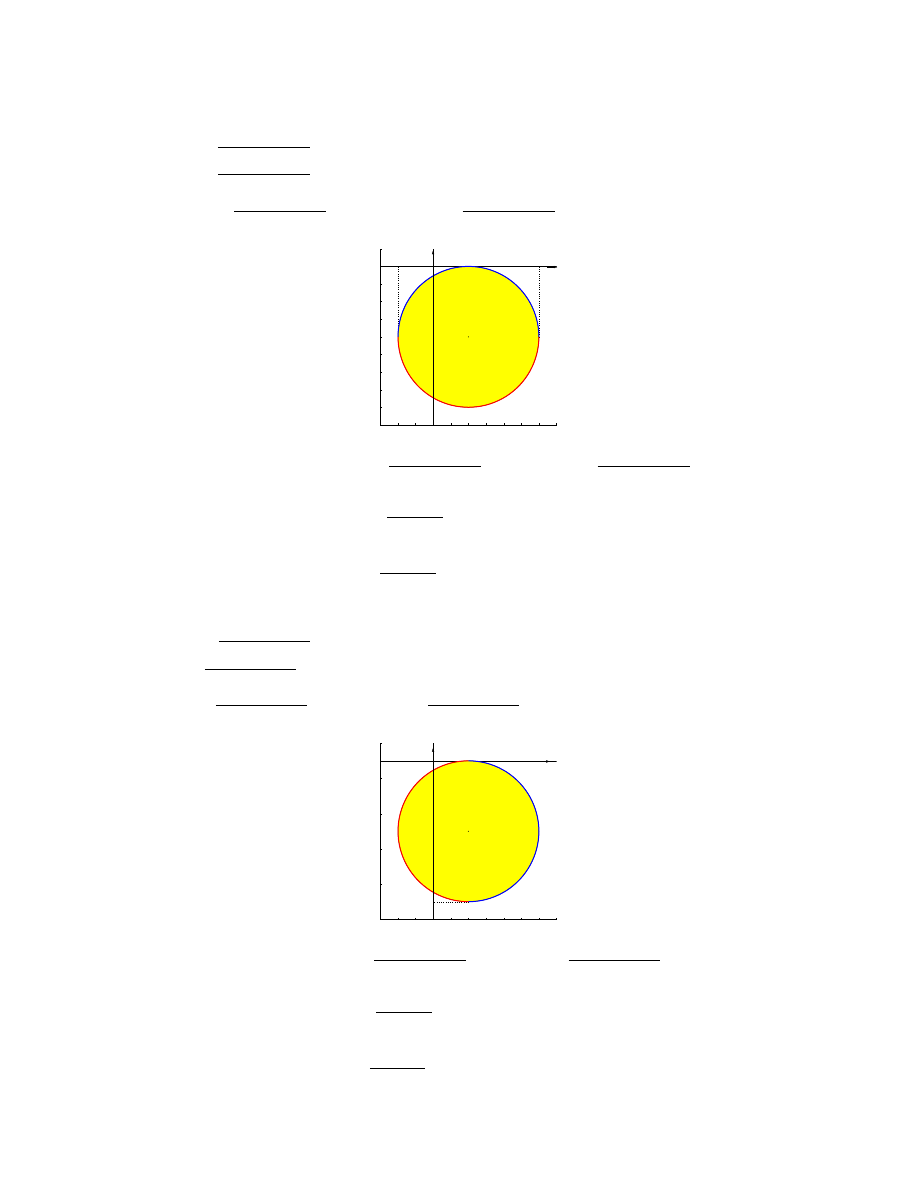
(c) (x − 1)

2

+ (y + 2)

2

= 4

• krzywa to okrąg o środku (1, −2) i promieniu 2

• wyznaczenie dolnej i górnej funkcji:

(x − 1)

2

+ (y + 2)

2

= 4

y + 2 = ±

q

4 − (x − 1)

2

y = −2 ±

q

4 − (x − 1)

2

, −1 ¬ x ¬ 3

d(x) = −2 −

q

4 − (x − 1)

2

, g(x) = −2 +

q

4 − (x − 1)

2

, −1 ¬ x ¬ 3

• rysunek

−1.5

−1

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

−4.5

−4

−3.5

−3

−2.5

−2

−1.5

−1

−0.5

0

0.5

−1

3

(1,−2)

y=−2+(4−(x−1)

2

)

1/2

y=−2−(4−(x−1)

2

)

1/2

0

y

x

• D to obszar normalny względem osi 0x, bo

D =

n

(x, y) : −1 ¬ x ¬ 3, −2 −

q

4 − (x − 1)

2

¬ y ¬ −2 +

q

4 − (x − 1)

2

o

• Stąd

Z Z

D

f (x, y) dxdy =

3

Z

−1

dx

−2+

√

4−(x−1)

2

Z

−2−

√

4−(x−1)

2

f (x, y)dy

• wyznaczenie lewej i prawej funkcji:

(x − 1)

2

+ (y + 2)

2

= 4

x − 1 = ±

q

4 − (y + 2)

2

x = 1 ±

q

4 − (y + 2)

2

, −4 ¬ y ¬ 0

l(y) = 1 −

q

4 − (y + 2)

2

, p(y) = 1 +

q

4 − (y + 2)

2

, −4 ¬ y ¬ 0

• rysunek

−1.5

−1

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

−4.5

−3.5

−2.5

−1.5

−0.5

0.5

y

x

(1,−2)

−4

0

x=1+(4−(y+2)

2

)

1/2

x=1−(4−(y+2)

2

)

1/2

• D to także obszar normalny względem osi 0y, bo

D =

n

(x, y) : −4 ¬ y ¬ 0, 1 −

q

4 − (y + 2)

2

¬ x ¬ 1 +

q

4 − (y + 2)

2

o

• Stąd

Z Z

D

f (x, y) dxdy =

0

Z

−4

dy

1+

√

4−(y+2)

2

Z

1−

√

4−(y+2)

2

f (x, y)dx

5

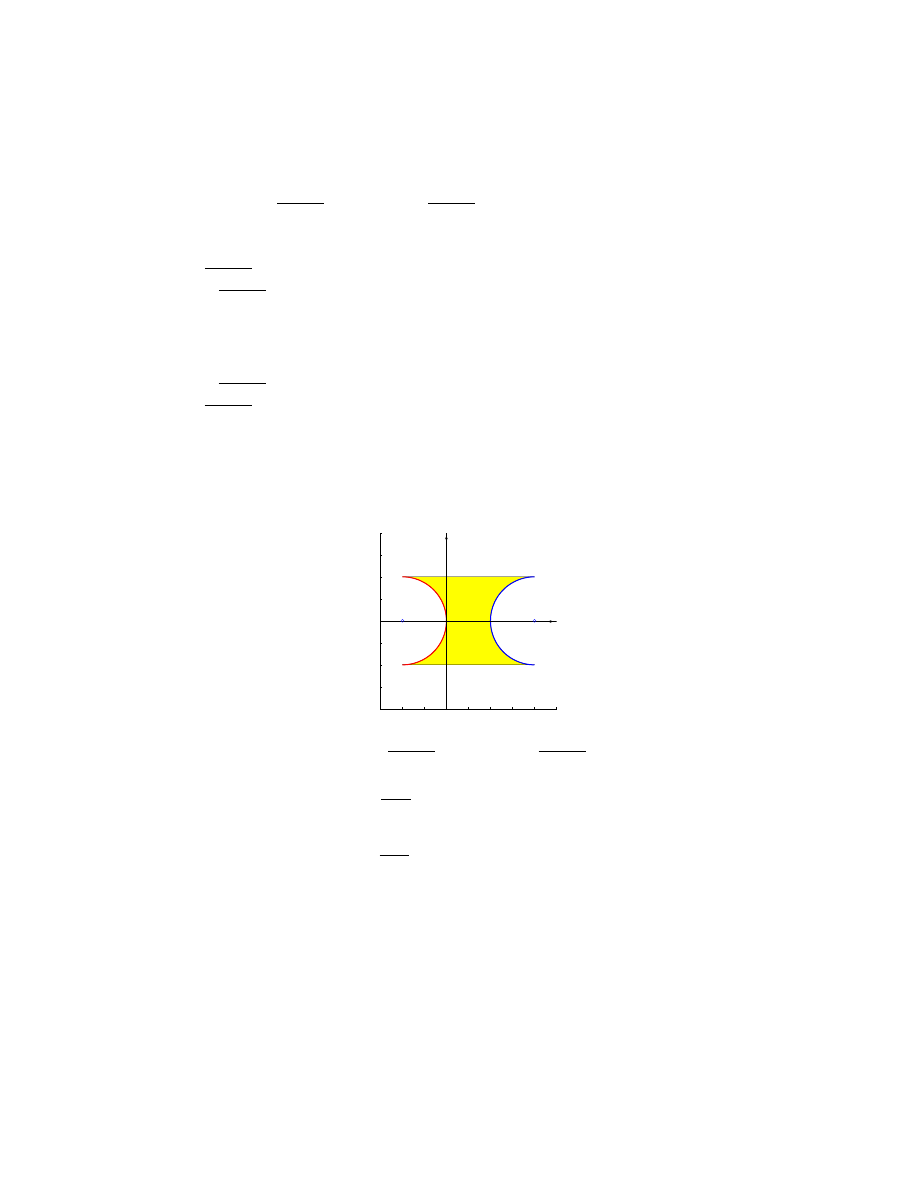
(d) y = −1, y = 1, x = 2 −

√

1 − y

2

, x = −1 +

√

1 − y

2

• dwie ostatnie krzywe to półokręgi:

x = 2 −

√

1 − y

2

x − 2 = −

√

1 − y

2

(x − 2)

2

= 1 − y

2

(x − 2)

2

+ y

2

= 1, x ¬ 2

lewy półokrąg o środku (2, 0) i promieniu 1

x = −1 +

√

1 − y

2

x + 1 =

√

1 − y

2

(x + 1)

2

= 1 − y

2

(x + 1)

2

+ y

2

= 1, x ­ 1

prawy półokrąg o środku (−1, 0) i promieniu 1

• rysunek

−1.5

−1

−0.5

0

0.5

1

1.5

2

2.5

−2

−1.5

−1

−0.5

0

0.5

1

1.5

2

y

x

(−1,0)

(2,0)

1

−1

x=2−(1−y

2

)

1/2

x=−1+(1−y

2

)

1/2

• D to obszar normalny względem osi 0y, bo

D =

n

(x, y) : −1 ¬ y ¬ 1, −1 +

√

1 − y

2

¬ x ¬ 2 −

√

1 − y

2

o

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

−1

dy

2−

√

1−y

2

Z

−1+

√

1−y

2

f (x, y)dx

6

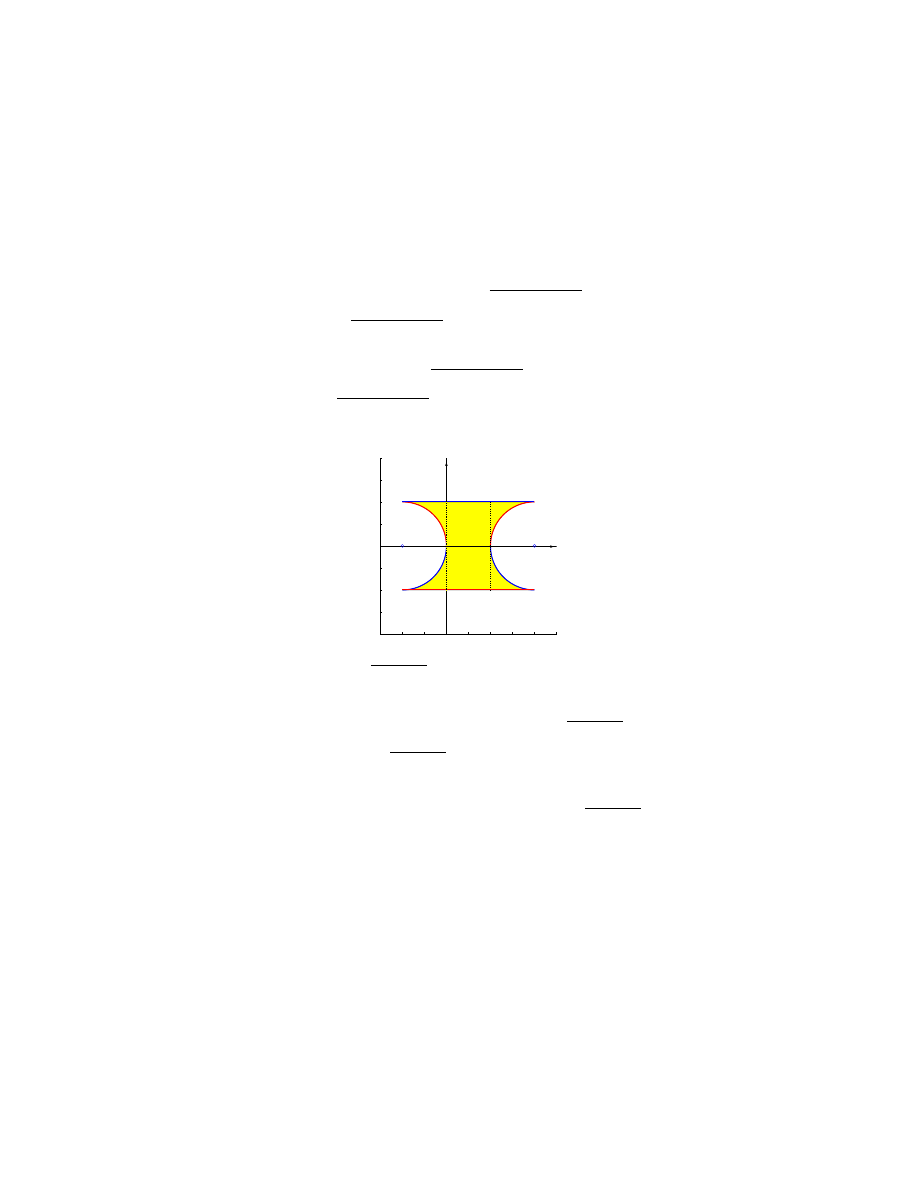
• D nie jest obszarem normalnym względem osi 0x, ale jest sumą takich obszarów o roz-

łącznych wnętrzach

D = D

1

∪ D

2

∪ D

3

∪ D

4

∪ D

5

gdzie D

1

=

n

(x, y) : −1 ¬ x ¬ 0, −1 ¬ y ¬ −

q

1 − (x + 1)

2

o

D

2

=

n

(x, y) : −1 ¬ x ¬ 0,

q

1 − (x + 1)

2

¬ y ¬ 1

o

D

3

= [0, 1] × [−1, 1]

D

4

=

n

(x, y) : 1 ¬ x ¬ 2, −1 ¬ y ¬ −

q

1 − (x − 2)

2

o

D

5

=

n

(x, y) : 1 ¬ x ¬ 2,

q

1 − (x − 2)

2

¬ y ¬ 1

o

• rysunek

−1.5

−1

−0.5

0

0.5

1

1.5

2

2.5

−2

−1.5

−1

−0.5

0

0.5

1

1.5

2

y

x

−1

0

1

2

y=1

y=−1

y=(1−(x−2)

2

)

1/2

y=−(1−(x−2)

2

)

1/2

y=(1−(x+2)

2

)

1/2

y=−(1−(x+2)

2

)

1/2

• Stąd

Z Z

D

f (x, y) dxdy =

0

Z

−1

dx

−

√

1−(x+1)

2

Z

−1

f (x, y)dy +

0

Z

−1

dx

1

Z

√

1−(x+1)

2

f (x, y)dy+

+

1

Z

0

dx

1

Z

−1

f (x, y)dy +

2

Z

1

dx

−

√

1−(x−2)

2

Z

−1

f (x, y)dy +

2

Z

1

dx

1

Z

√

1−(x−2)

2

f (x, y)dy

7

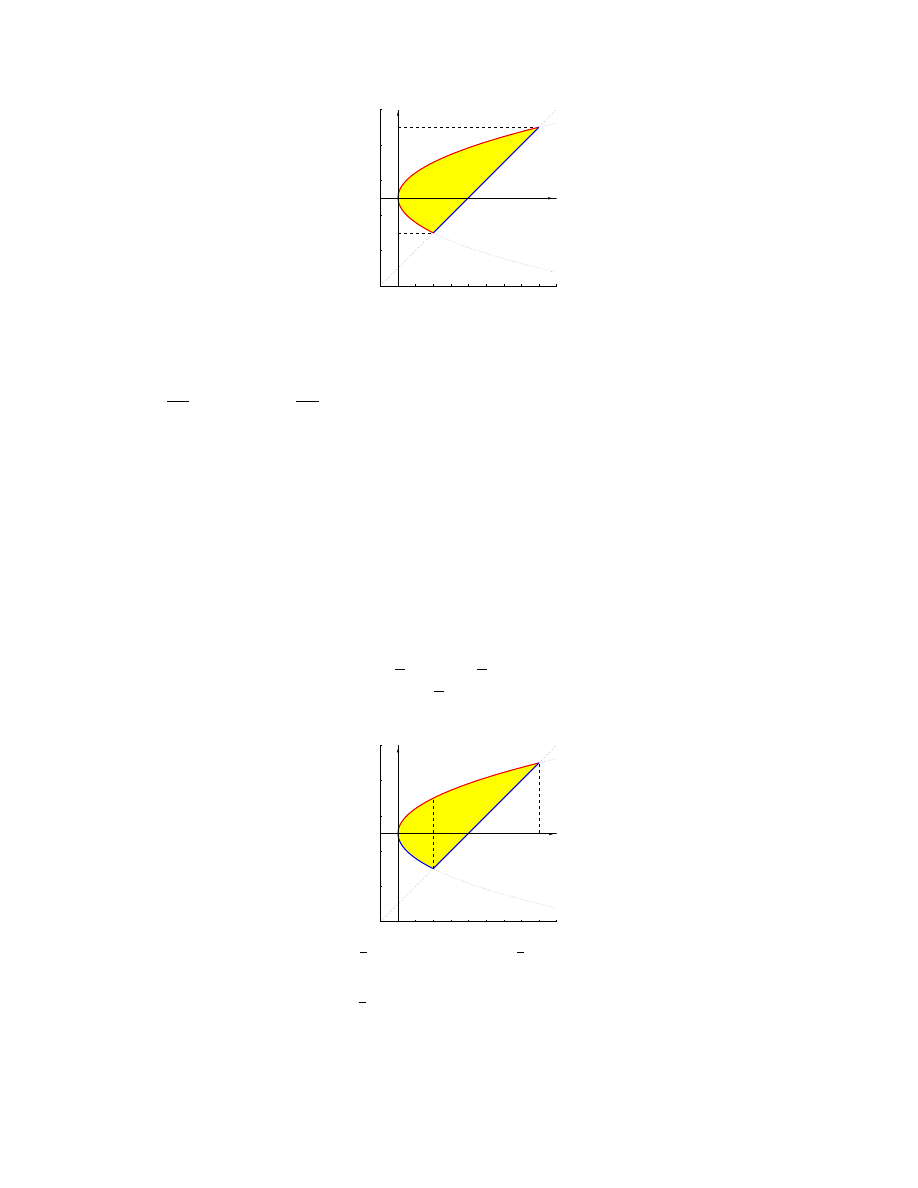
(e) x = y

2

, y = x − 2

• D to obszar między parabolą x = y

2

a prostą x = y + 2

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

−2.5

−1.5

−0.5

0.5

1.5

2.5

x

y

−1

2

x=y

2

x=y+2

• szukamy punktów wspólnych tych krzywych:

y

2

= y + 2

y

2

− y − 2 = 0

∆ = 9
y

1

=

1−3

2

= −1, y

2

=

1+3

2

= 2

• D to obszar normalny względem osi 0y, bo

D = {(x, y) : −1 ¬ y ¬ 2, y

2

¬ x ¬ y + 2 }

• Stąd

Z Z

D

f (x, y) dxdy =

2

Z

−1

dy

y+2

Z

y

2

f (x, y)dx

• D jest też obszarem normalnym względem osi 0x, wygodniej przedstawić go jako sumę

takich obszarów o rozłącznych wnętrzach

D = D

1

∪ D

2

gdzie D

1

= {(x, y) : 0 ¬ x ¬ 1, −

√

x ¬ y ¬

√

x }

D

2

= {(x, y) : 1 ¬ x ¬ 4, x − 2 ¬ y ¬

√

x }

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

−2.5

−1.5

−0.5

0.5

1.5

2.5

y

x

y=x−2

y=x

1/2

y=−x

1/2

4

1

0

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

0

dx

√

x

Z

−

√

x

f (x, y)dy +

4

Z

1

dx

√

x

Z

x−2

f (x, y)dy

8

(f) x = 0, y = e

2

, y = e

x

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

−1

0

1

2

3

4

5

6

7

8

y

x

2

e

2

1

0

y=e

2

x=ln(y)

y=e

x

x=0

• D to obszar normalny względem osi 0x, bo

D = {(x, y) : 1 ¬ y ¬ e

2

, 0 ¬ x ¬ ln y}

• Stąd

Z Z

D

f (x, y) dxdy =

e

2

Z

1

dy

ln y

Z

0

f (x, y)dx

• x = ln y ⇐⇒ y = e

x

• Zatem D to także obszar normalny względem osi 0y, bo

D = {(x, y) : 0 ¬ x ¬ 2, e

x

¬ y ¬ e

2

}

• Stąd

Z Z

D

f (x, y) dxdy =

2

Z

0

dx

e

2

Z

e

x

f (x, y)dy

9

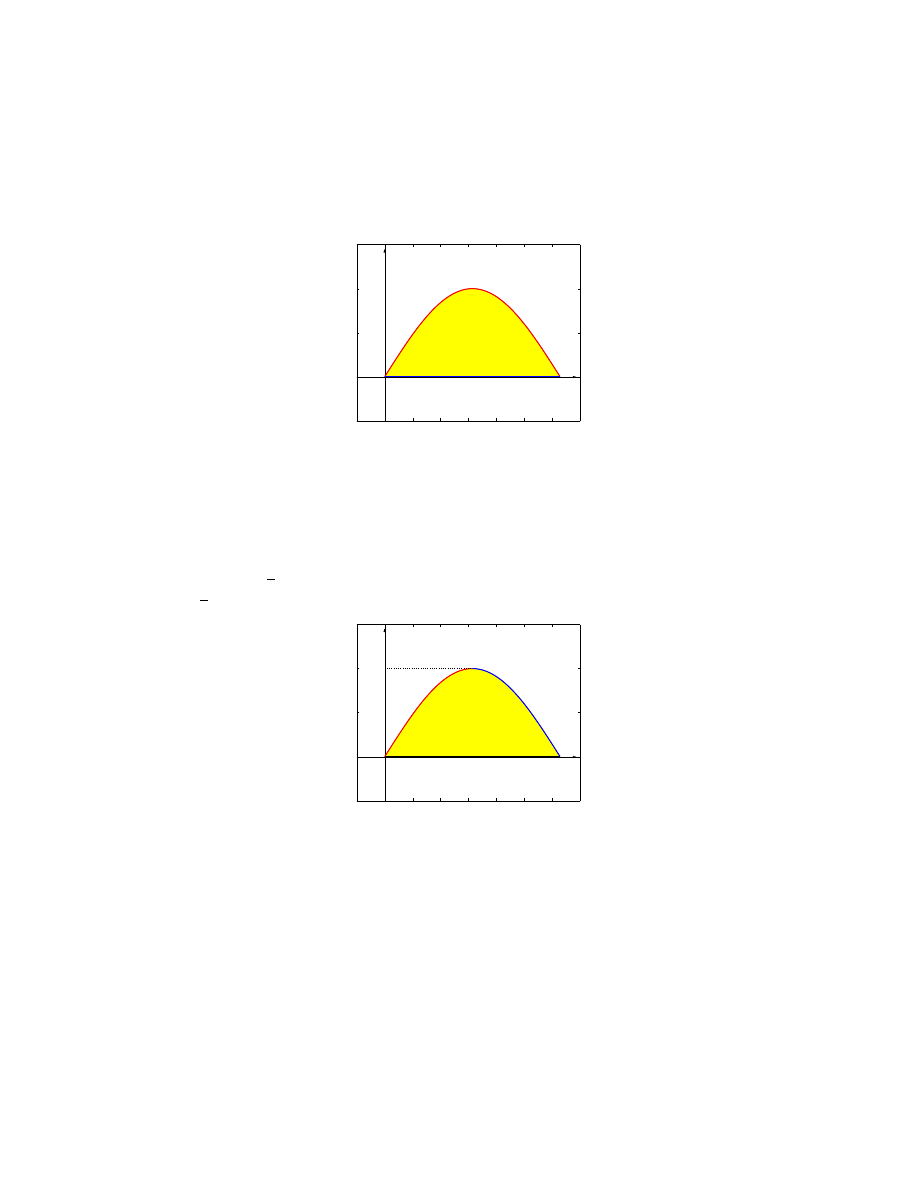
(g) y = 0, y = sin x, przy czym 0 ¬ x ¬ π

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

−0.5

0

0.5

1

1.5

y

x

y=sin(x)

y=0

π

0

• D to obszar normalny względem osi 0x, bo

D = {(x, y) : 0 ¬ x ¬ π, 0 ¬ y ¬ sin x}

• Stąd

Z Z

D

f (x, y) dxdy =

π

Z

0

dx

sin x

Z

0

f (x, y)dy

• y = sin x, 0 ¬ x ¬

π

2

⇐⇒ x = arc sin y, 0 ¬ y ¬ 1

y = sin x,

π

2

¬ x ¬ π ⇐⇒ x = π − arc sin y, 0 ¬ y ¬ 1

• rysunek

−0.5

0

0.5

1

1.5

2

2.5

3

3.5

−0.5

0

0.5

1

1.5

y

x

1

0

x=

π

−arcsin(x)

x=arcsin(x)

• Zatem D to także obszar normalny względem osi 0y, bo

D = {(x, y) : 0 ¬ y ¬ 1, arc sin y ¬ x ¬ π − arc sin y}

• Stąd

Z Z

D

f (x, y) dxdy =

1

Z

0

dy

π−arc sin y

Z

arc sin y

f (x, y)dx

10

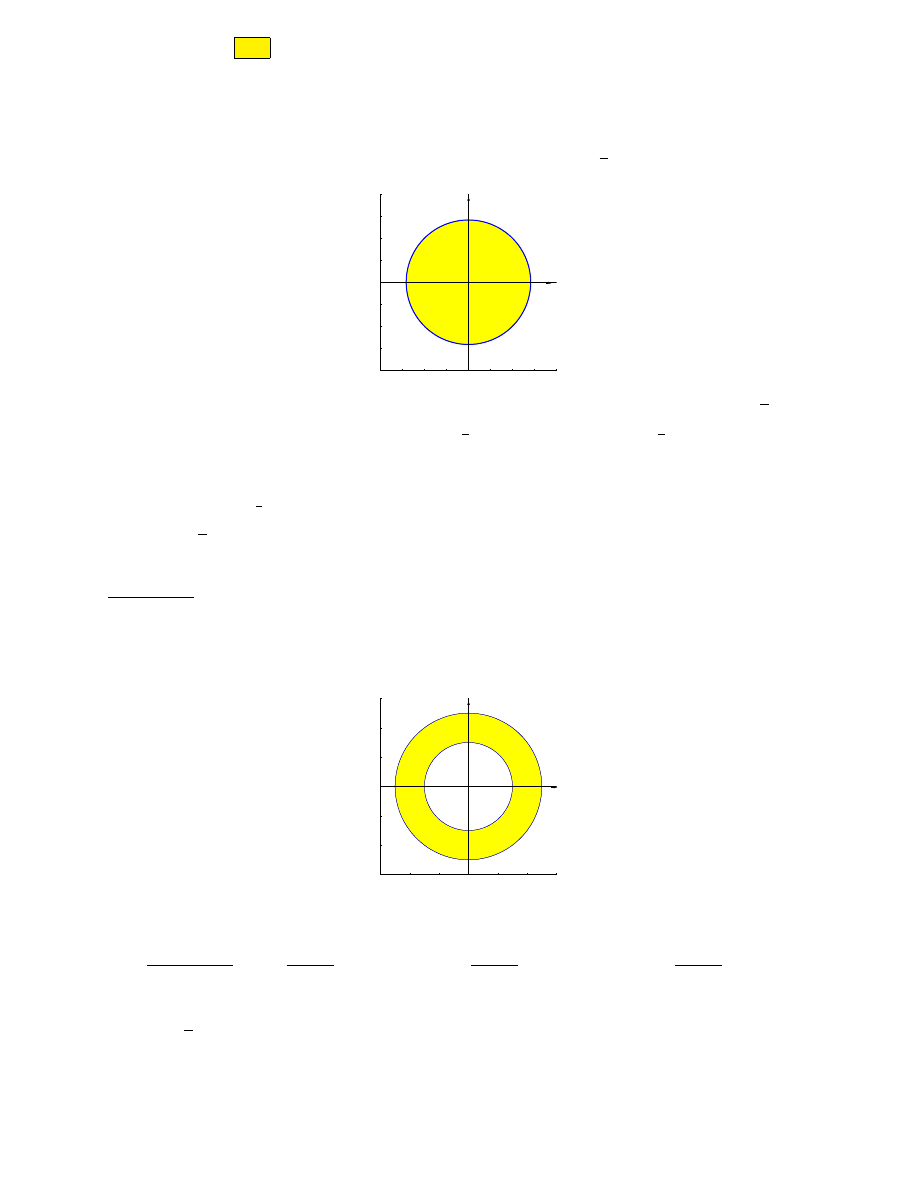
Przykłady do zadania 1.4 :
Wprowadzając współrzędne biegunowe obliczyć podane całki podwójne po wskazanych obszarach:

(a)

Z Z

D

e

−(x

2

+y

2

)

dxdy, gdzie D to obszar ograniczony krzywą x

2

+ y

2

= 2

• D = {(x, y) : x

2

+ y

2

¬ 2} - koło o środku (0, 0) i promieniu

√

2

−2

−1.5

−1

−0.5

0

0.5

1

1.5

2

−2

−1.5

−1

−0.5

0

0.5

1

1.5

2

x

y

2

1/2

• D we współrzędnych biegunowych odpowiada ∆ = {(ϕ, ρ) : 0 ¬ ϕ ¬ 2π, 0 ¬ ρ ¬

√

2}

•

Z Z

D

e

−(x

2

+y

2

)

dxdy =

Z Z

∆

e

−ρ

2

ρ dρdϕ =

2π

Z

0

dϕ

√

2

Z

0

e

−ρ

2

ρ dρ =





2π

Z

0

dϕ





·






√

2

Z

0

e

−ρ

2

ρ dρ






=

= 2π ·





−

1

2

e

−ρ

2

√

2

0

= π(1 − e

−2

)

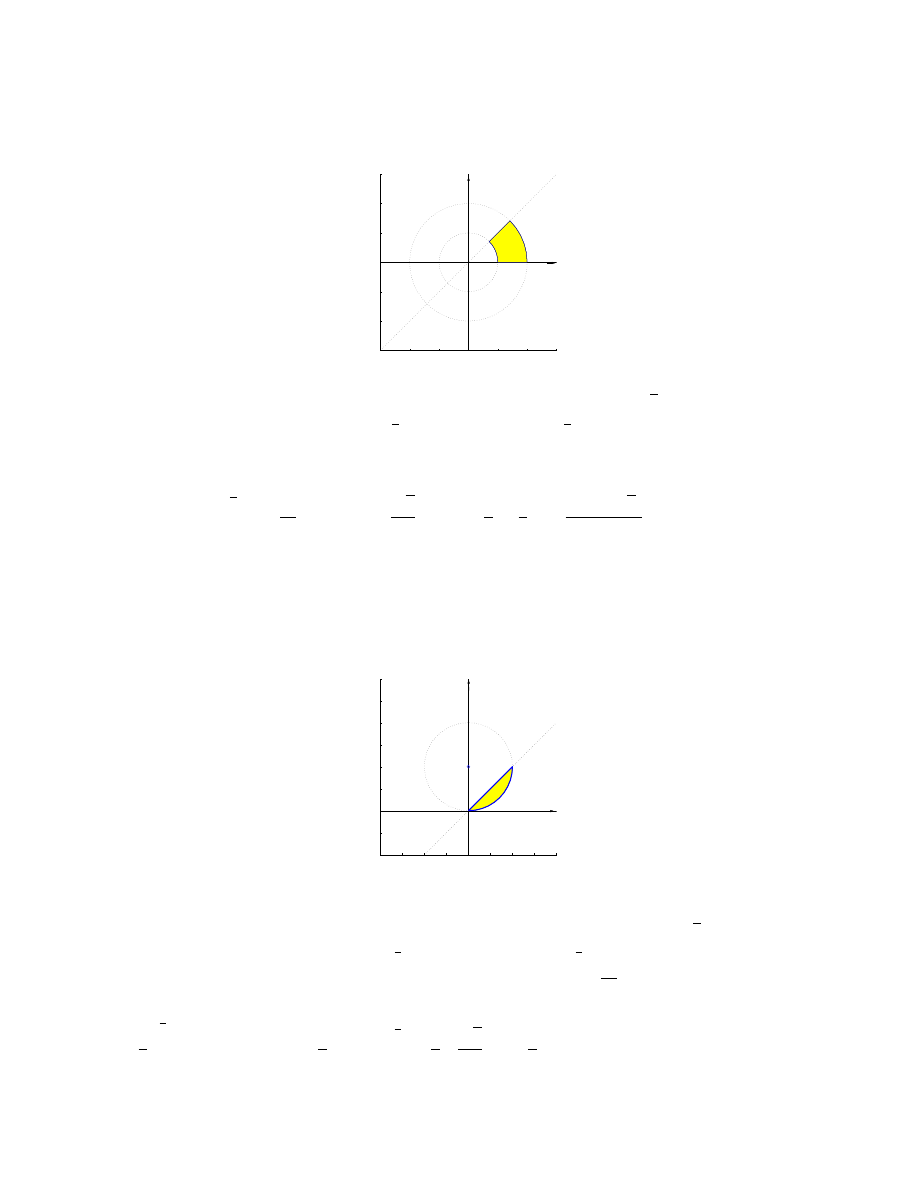
(b)

Z Z

D

dxdy

x

2

+ y

2

− 1

, gdzie D to obszar ograniczony krzywymi x

2

+ y

2

= 9 i x

2

+ y

2

= 25

• D = {(x, y) : 9 ¬ x

2

+y

2

¬ 25} - pierścień kołowy o środku (0, 0) i promieniu wewnętrznym

3, zewnętrznym 5

−6

−4

−2

0

2

4

6

−6

−4

−2

0

2

4

6

y

x

3

5

• D we współrzędnych biegunowych odpowiada ∆ = {(ϕ, ρ) : 0 ¬ ϕ ¬ 2π, 3 ¬ ρ ¬ 5}

•

Z Z

D

dxdy

x

2

+ y

2

− 1

=

Z Z

∆

1

ρ

2

− 1

ρ dρdϕ =

2π

Z

0

dϕ

5

Z

3

ρ

ρ

2

− 1

dρ =





2π

Z

0

dϕ





·





5

Z

3

ρ

ρ

2

− 1

dρ





=

= 2π ·





1

2

ln |ρ

2

− 1|

5

3

= π(ln 24 − ln 8) = π ln 3

11

(c)

Z Z

D

y dxdy, gdzie D to obszar ograniczony krzywymi x

2

+ y

2

= 1, x

2

+ y

2

= 4, y = x, y = 0,

(x, y ­ 0)

• D = {(x, y) : 1 ¬ x

2

+ y

2

¬ 4, 0 ¬ y ¬ x} - wycinek pierścienia kołowego o środku (0, 0) i

promieniu wewnętrznym 1, zewnętrznym 2

−3

−2

−1

0

1

2

3

−3

−2

−1

0

1

2

3

y

x

2

1

y=x

y=0

• D we współrzędnych biegunowych odpowiada ∆ =

n

(ϕ, ρ) : 0 ¬ ϕ ¬

π

4

, 1 ¬ ρ ¬ 2

o

•

Z Z

D

y dxdy =

Z Z

∆

(ρ sin ϕ) ρ dρdϕ =

π

4

Z

0

dϕ

2

Z

1

ρ

2

sin ϕ dρ =






π

4

Z

0

sin ϕ dϕ






·





2

Z

1

ρ

2

dρ





=

=





− cos ϕ

ϕ=

π

4

ϕ=0





·





ρ

3

3

ρ=2

ρ=1





=

−

√

2

2

+ 1

!

·

8

3

−

1

3

=

7(2 −

√

2)

3

(d)

Z Z

D

x dxdy, gdzie D to obszar ograniczony krzywymi x

2

+ (y − 1)

2

= 1, y = x, (x ­ y)

• D = {(x, y) : x

2

+ (y − 1)

2

¬ 1, 0 ¬ y ¬ x} - fragment koła o środku (0, 1) i promieniu 1

leżący poniżej prostej y = x

−2

−1.5

−1

−0.5

0

0.5

1

1.5

2

−1

−0.5

0

0.5

1

1.5

2

2.5

3

y

x

1

y=x

• x

2

+ (y − 1)

2

¬ 1 ⇐⇒ x

2

+ y

2

¬ 2y ⇐⇒ ρ

2

¬ 2ρ sin ϕ ⇐⇒ ρ ¬ 2 sin ϕ

Zatem D we współrzędnych biegunowych odpowiada ∆ =

n

(ϕ, ρ) : 0 ¬ ϕ ¬

π

4

, 0 ¬ ρ ¬ 2 sin ϕ

o

•

Z Z

D

x dxdy =

Z Z

∆

(ρ cos ϕ) ρ dρdϕ =

π

4

Z

0

dϕ

2 sin ϕ

Z

0

ρ

2

cos ϕ dρ =

π

4

Z

0





ρ

3

3

ρ=2 sin ϕ

ρ=0





cos ϕ dϕ =

=

2

3

π

4

Z

0

4 sin

3

ϕ cos ϕ dϕ =

2

3





sin

4

ϕ

π

4

0

=

2

3

√

2

2

!

4

=

1

6

12