3.7. Różniczka funkcji

Definicja

Niech y = f(x) będzie funkcją określoną w zbiorze Df ⊂ R, x i x0 różnymi liczbami jej dzie-dziny oraz funkcja f ma pochodną w punkcie x0.

• Przyrostem argumentu od x0 do x nazywamy liczbę ∆ x = x – x0 .

• Przyrostem wartości funkcji w punkcie x0 przy przyroście argumentu ∆x

nazywamy liczbę ∆f∆x(x0) = f(x0 + ∆x) – f(x0).

• Różniczką funkcji y = f(x) w punkcie x0 (oznaczenie df( x) lub dy ) dla przyrostu argumentu ∆ x = x – x0

nazywamy wyrażenie df( x) = f ’( x0) ( x – x0); czyli df( x) = f ’( x0) ∆ x .

Zauważ, że różniczka danej funkcji w danym punkcie x0 jest funkcją argumentu x zależ-

ną od wartości pochodnej tej funkcji w punkcie x0 oraz przyrostu ∆ x argumentów od x0 do x .

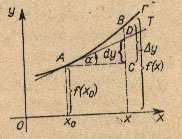
Rysunek przedstawia krzywą Γ, będącą wykresem funkcji y = f(x) , styczną T do tej krzywej

w punkcie A, f(x0) – wartość funkcji w punkcie x0, f(x) – wartość funkcji w punkcie x,

∆y – przyrost wartości funkcji (odcinek CB) oraz dy – różniczkę funkcji (odcinek CD)

Przykłady

a) Różniczka funkcji sinus w punkcie x0 jest funkcją daną wzorem d sin x = ( x – x0) cos x0 .

π

π

π

π

Jeśli, np. x0 =

, to d sin x = ( x –

) cos

= ½ ⋅ ( x –

).

3

3

3

3

π

Czyli d sin x = ½ ⋅ ( x –

).

3

π

π

π

π

π

π

Wartość tej funkcji w x =

, wynosi d sin

= ½ ⋅ (

–

) = ½ ⋅

=

.

2

3

2

3

6

12

π

π

Stąd d sin

=

.

3

12

π

π

Wartość tej funkcji w x = 0, wynosi d sin 0 = ½ ⋅ (0 –

) = –

.

3

6

π

Stąd d sin 0 = –

.

6

b) Różniczka funkcji f(x) = x w punkcie x0 jest równa

d f(x) = dx = (x)’ (x – x0) = x – x0 = ∆ x.

Czyli dx = ∆ x.

Wykorzystując fakt, że dx = ∆ x możemy napisać (dla dowolnej funkcji f):

df ( x)

d f(x) = f ’(x) dx oraz f ’(x) =

dx

Słownie ten związki możemy wyrazić następująco:

a) różniczka funkcji f w punkcie x jest iloczynem pochodnej funkcji i przyrostu argumentu,

b) pochodna funkcji jest ilorazem różniczek funkcji i różniczki argumentu.

Uwagi

1. Przyrost wartości funkcji ∆f∆x(x0) informuje, jaki błąd popełniamy biorąc f(x0 + ∆x)

zamiast f(x0), gdy argument wzrasta o ∆x.

2. Można udowodnić, że różniczka funkcji f jest wartością przybliżoną przyrostu funkcji,

przy czym przybliżenie jest tym lepsze, im mniejszy jest przyrost argumentu dx = ∆x,

czyli d f(x0) ≈ ∆f(x0),

czyli d f(x0) ≈ f(x0 + ∆x) – f(x0) albo f ’(x0) dx ≈ f(x0 + ∆x) – f(x0).

Przykłady

a)

Oblicz różniczkę funkcji f(x) = x3 i porównaj ją z przyrostem dla x = 10 i dx = 0,02

Rozwiązanie

Różniczka funkcji df = d x3 = 3x2 dx.

Podstawiając dane wartości mamy df = 3⋅ 100 ⋅0,02 = 6,

natomiast przyrost ∆f = (10,02)3 – 103 = 1006,012 – 1000 = 6,012.

Widzimy, że różnica pomiędzy przyrostem i różniczką wynosi tylko 0,012.

b) Podaj, wykorzystując pojęcie różniczki funkcji przybliżenie liczby

,

9 09 .

Rozwiązanie

1

Wygodnie, w tym przypadku rozważyć funkcję y = x . Różniczka dy =

dx.

2 x

Przyjmijmy, że x = 9 oraz dx = 0,09.

Wtedy

,

9 09 można przedstawić jako y + ∆ y, a dla uproszczenia obliczeń ∆ y można 1

zastąpić przez różniczkę dy. Różniczka dy =

dx.

2 x

1

Podstawiając do wzoru dy =

dx mamy:

2 x

1

dy =

⋅ 0,09 = 0,015, a więc

,

9 09 = 3 + 0,015 = 3,015.

6

Obliczając liczbę

,

9 09 z dokładnością do 6 cyfr po przecinku mamy

,

9 09 = 3,014963.

Zastosowanie różniczki do szacowania błędów

Często wykonuje się pomiar pewnej wielkości po to, aby na tej podstawie wyznaczyć

wartość innej wielkości, np. mierzymy średnicę kuli, aby obliczyć jej objętość.

Niech x oznacza wynik pomiaru, a y wielkość obliczoną ze wzoru y = f(x). Wynik pomiaru jest obciążony pewnym błędem dx, którego wielkość zależy od dokładności przyrzą-

dów pomiarowych, umiejętności mierzącego i wielu innych czynników.

Błąd obciążający pomiar x pociąga za sobą błąd ∆ y wielkości obliczonej y. Jeżeli nie znamy błędu dx, to nie potrafimy też określić znaku błędu ∆ y, a taka sytuacja w praktyce zda-rza się najczęściej. Poprzestajemy wtedy na szacowaniu wartości bezwzględnej błędu. Przy

dokładnym mierzeniu błąd dx bywa zwykle niewielki, co pozwala zastąpić wielkość ∆ y przez różniczkę dy. Zwykle znajomość przyrządu pomiarowego pozwala określić maksymalną moż-

liwą wielkość błędu, jaki można popełnić przy mierzeniu x.

Jeżeli przez dx oznaczymy maksymalny błąd pomiaru x, to wartość bezwzględną mak-symalnego błędu obciążającego y obliczamy według wzoru:

δy = |dy| = |f’(x)dx|, gdzie δ y oznacza błąd maksymalny.

Przykłady

1. Oceń błąd, jaki popełniono obliczając objętość kostki sześciennej, gdy w wyniku pomiaru krawędzi otrzymano x = 7,4 cm, a błąd maksymalny dx = 0,03 cm.

Rozwiązanie.

Objętość sześcianu obliczamy ze wzoru y = x3 . Błąd maksymalny objętości obliczymy

z różniczki dy = 3x2 dx .

Podstawiając dane otrzymujemy:

δy = |dy| = | 3x2 dx| = 3⋅ 7,42 ⋅ 0,03 = 4,9284 .

Błąd względny wynosi:

dy

9

,

4 284

=

= 0,09 = 9%.

y

2

7,4

Błąd obliczenia wynosi 9% .

2. Odległość między miejscowościami A i B położonymi na przeciwległych zboczach doliny w linii powietrznej wynosi m. Najkrótsza ścieżka przez dolinę między A i B

ma długość s. Maksymalna odległość od dna doliny do poziomu AB wynosi a.

Określ, jak zmiana wysokości a o ∆ a wpływa na zmianę długości ścieżki ∆ s.

m

A

B

a

s

Rozwiązanie

W rozważaniach teoretycznych przyjmuje się, że odległość s zależy od odległości

m między A i B oraz wysokości a . Opisuje ją wzór:

8

2

a

8

s ≈ m 1

( + ⋅

) =

2

m +

a .

3

2

m

3 m

16

Obliczamy różniczkę funkcji s zmiennej a: ds =

a d a.

m

3

16

Stąd ∆s ≈

a ⋅∆ a.

m

3

16

Czyli, jeśli a zmieni się o ∆ a , to ∆s zmieni się o

a ⋅∆ a.

m

3

Na przykład, jeśli w wyniku potężnej ulewy i osunięcia się ziemi pierwotna odległość

od dna doliny do poziomu AB wynosząca a 120 metrów zmniejszyła się o ⋅∆ a = 2 metry, 1280

1280

wówczas długość s ścieżki zmieniła się o ∆s = -

metrów, jest krótsza o

metrów.

m

m

Zadania do samodzielnego rozwiązywania

Zadanie 1.

Oblicz przyrost ∆f wartości funkcji f w punkcie x0 przy przyroście argumentu ∆x.

Zbadaj, jak zmieni się przyrost ∆f, gdy przyrost argumentu podwoi się.

a) f(x) = 2x+7 , x0 = 3, ∆x = 2 , b) f(x) = x2 +6x + 4 , x0 = 2, ∆x = -1 ,

c) f(x) = 2x+1 , x0 = 1, ∆x = 1 , d) f(x) = ln x , x0 = 4, ∆x = -0,01 .

Zadanie 2.

Wyraź wzorem różniczkę df funkcji f , gdy:

a) f(x) = x3 , b) f(x) = x , c) f(x) = - 3x+17 , d) f(x) = 21 – 4x,

− 3 x +1

e) f(x) =

, f) f(x) = (-x +3)12 , g) f(x) = x2 e-x .

2

x +1

Zadanie 3.

Wyznacz przyrost ∆f oraz różniczkę df funkcji f w punkcie x0 przy przyroście argu-

mentu dx . Porównaj obliczone wielkości, gdy:

a) f(x) = x2 – 2x + 5, x0 = 1 i dx = 1 ; x0 = 1 i dx = 0,1 ;

b) f(x) = 2x2 + x-1, x0 = 1 i dx = 0,01 ; x0 = 1 i dx = 0,1 ;

c) f(x) = x2 + 3x, x0 = 1 i dx = 0,02 ; x0 = 1 i dx = 0,2 .

Zadanie 4.

Wykorzystując pojęcie różniczki funkcji wyznacz przybliżenie liczby:

a) 4 15 9

, 6 , b) e-0,01 , c)cos 0,03 , d) arc tg 1,005. Otrzymane przybliżenia po-

równaj z wynikami uzyskanymi z użyciem komputera.

Odpowiedzi

Zad. 1.: a) ∆f2(3) = 4 , ∆f4(3)= 8 , b) ∆f-1(2) = -9 , ∆f-2(2) = -18 , c) ∆f1(1) = 4,

∆f2(1) = 12, d) ∆f-0,01(4) = - 0,0025, ∆f-0,02(4) = -0,005.

Zad. 2.: a) df = 3x2dx , b) df = 2-1,5dx , c) df = -3dx, d) df = -4 dx,

2

3 x − 2 x − 3

e) df =

dx , f) df = -12(3-x)11 dx , g) df = (2xe-x – x2e-x)dx .

2

2

( x + )

1

Zad. 3.: a) ∆f1(1) = 1, df(1)= 0; ∆f0,1(1) = 0,01, df(1) = 0 ; b) ∆f0,01(1) ≈ 0,030299,

df(1) = 0,03; ∆f0,1(1) ≈ 0,329 ; c) ∆f0,02(1) = 0,1004, ∆f0,2(1) = 1,04 .

Zad. 4.: a) 1,9987 , b) 0,99 , c) 0,9995 , d) 0,7879 .