PROGNOZA ILOŚCI MIESZKAŃ

ODDANYCH DO UŻYTKU

Anna Rzempołuch

Sylwia Sprycha

Katarzyna Szabłowska

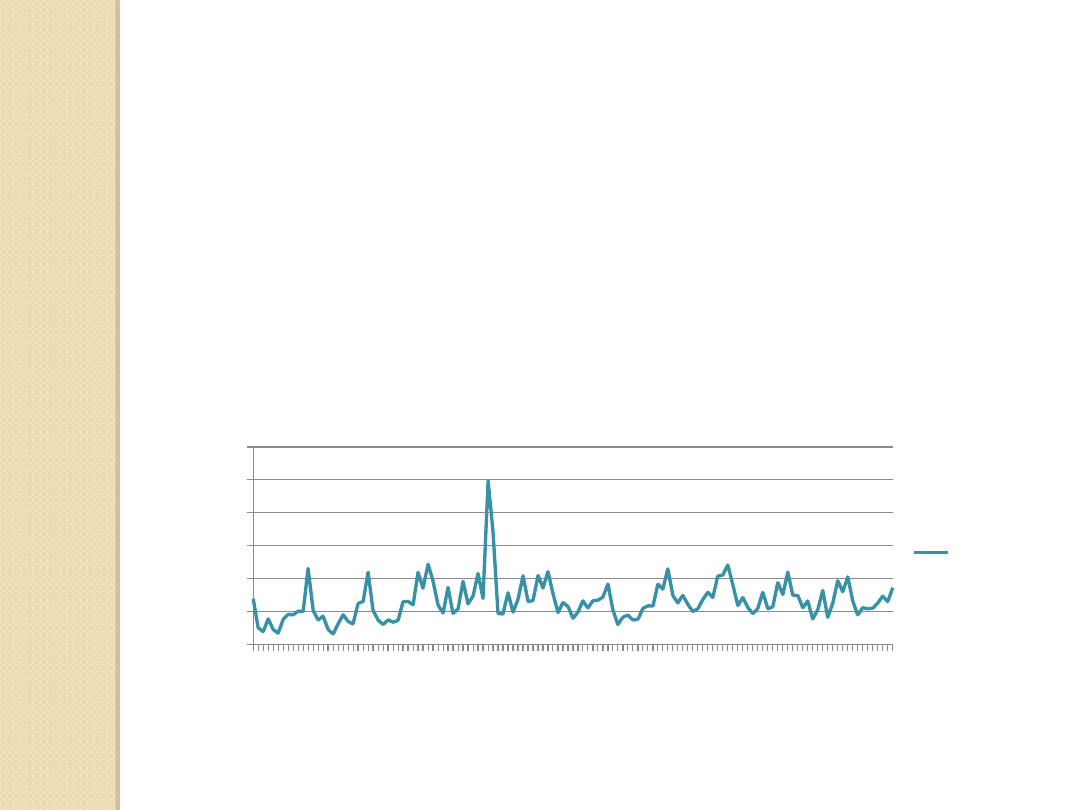
Celem przeprowadzonego badania jest sporządzenie prognozy
dla analizowanego zjawiska jakim jest ilość mieszkań oddanych
do użytkowania. Zebrane dane zostały przedstawione w ujęciu
miesięcznym, obejmują 10 lat i 9 miesięcy, zatem ich zakres
obejmuje 129 uporządkowanych chronologicznie wartości.
Dane będące przedmiotem badania pochodzą z bazy Głównego
Urzędu Statystycznego. Obejmują ilość mieszkań oddanych do
użytkowania w poszczególnych miesiącach, na przestrzeni lat
2005-2015.

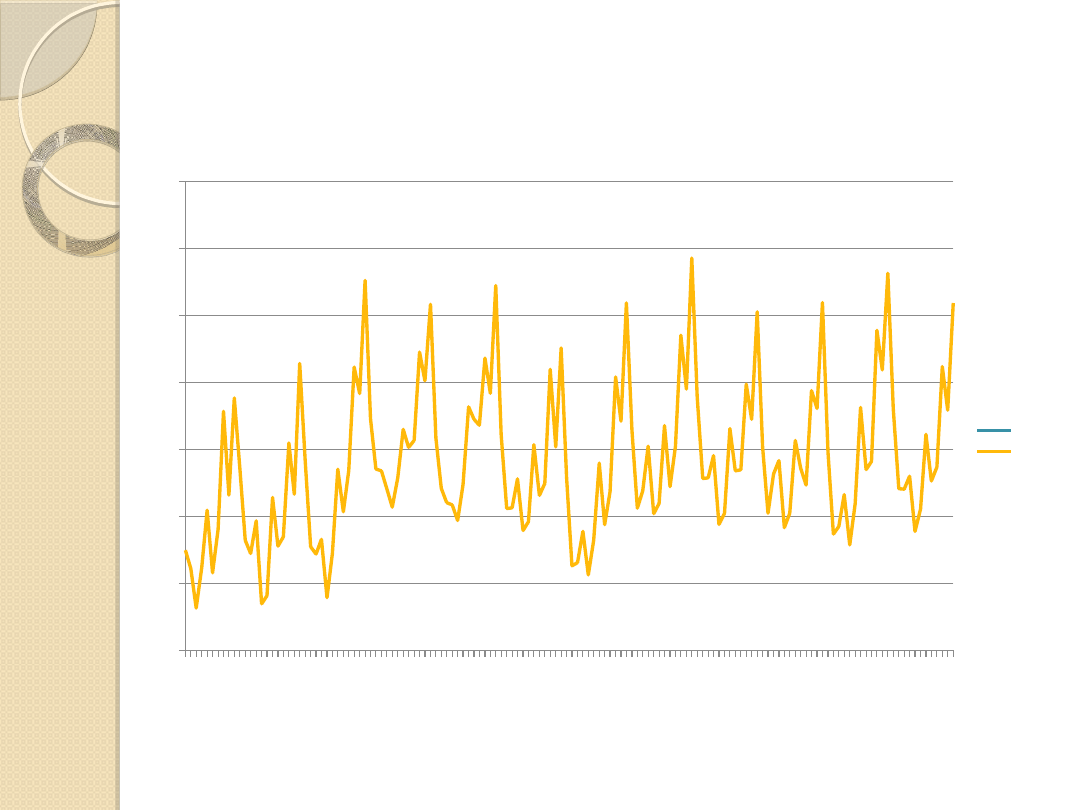
Wykres 1. Mieszkania oddane do użytkownika (w tys.)

Źródło: Opracowanie własne

I 2

00

5

VI

2

00

5

XI

20

05

IV

2

00

6

IX

20

06

II 2

00

7

VI

I 2

00

7

XII

2

00

7

V

20

08

X

20

08

III

20

09

VI

II 2

00

9
I 2

01

0

VI

2

01

0

XI

20

10

IV

2

01

1

IX

20

11

II 2

01

2

VI

I 2

01

2

XII

2

01

2

V

20

13

X

20

13

III

20

14

VI

II 2

01

4
I 2

01

5

VI

2

01

5

5 000

10 000

15 000

20 000

25 000

30 000

35 000

Yt

I 2

00

5

VI

2

00

5

XI

20

05

IV

2

00

6

IX

20

06

II 2

00

7

VI

I 2

00

7

XII

2

00

7

V

20

08

X

20

08

III

20

09

VI

II 2

00

9

I 2

01

0

VI

2

01

0

XI

20

10

IV

2

01

1

IX

20

11

II 2

01

2

VI

I 2

01

2

XII

2

01

2

V

20

13

X

20

13

III

20

14

VI

II 2

01

4

I 2

01

5

VI

2

01

5

5 000

7 000

9 000

11 000

13 000

15 000

17 000

19 000

Yt

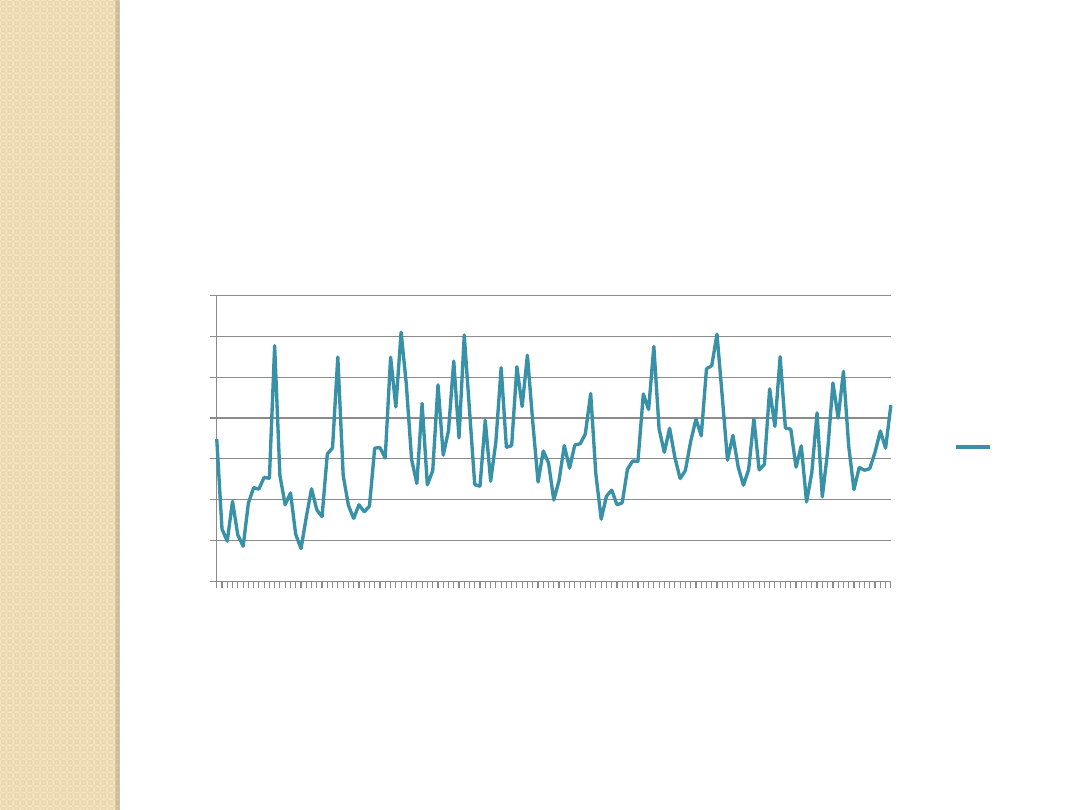
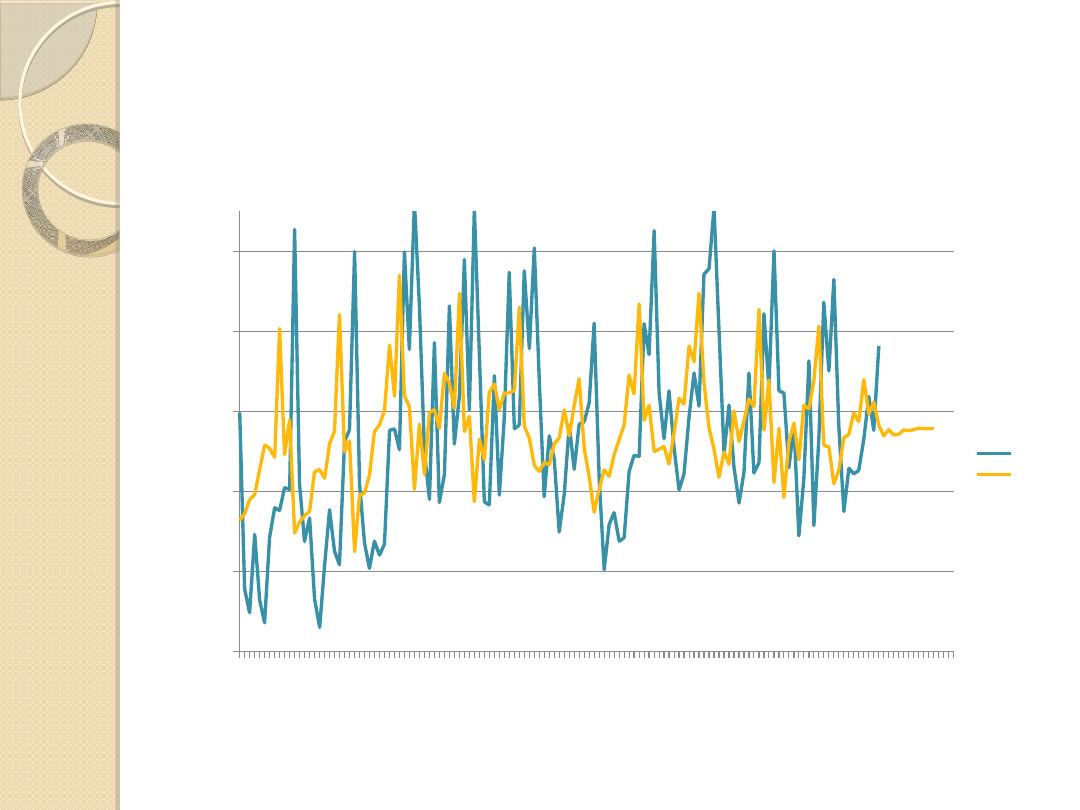
Wykres 2. Mieszkania oddane do użytkownika (w tys.) – szereg czasowy, z

wyeliminowaną zmienną odstającą

.

Źródło: Opracowanie własne

Opis stosowanych metod prognozy

Do wyznaczenie prognozy na podstawie analizowanych danych

zostaną zastosowane trzy metody wyznaczania prognozy:



Metoda wskaźników sezonowości;



Metoda ARIMA;



Model autoregresji.

 

Metoda wskaźników
sezonowości

Polega na wyznaczeniu wskaźników sezonowości poszczególnych faz
cyklu. Prognozę wyznacza się na podstawie funkcji trendu
skorygowanej o wskaźnik sezonowości.

Etapy:
-Obliczenie średniej ruchomej SRc
-Obliczenie wartości teoretycznych i średniej ruchomej centrowanej Yt-

SRc;

-Obliczenie surowych wskaźników sezonowości St^ jako średnich

wartości dla każdego miesiąca;

-Obliczenie współczynnika korekty K jako sumy średnich wartości dla

każdego miesiąca podzielonej przez liczbę okresów, czyli 12;

-Wyodrębnienie czynnika sezonowego S poprzez oczyszczenie surowych

wskaźników za pomocą współczynnika korekt. W modelu addytywnym
ich suma wynosi 0;

-Budowa szeregu skorygowanego z wahań sezonowych Yt-St;
-Obliczenie funkcji trendu;
-Wyznaczenie prognozy.

Metoda ARIMA

Jest to model szeregów czasowych znanych jako model
autoregresji oraz średniej ruchomej, używany jest do
modelowania szeregów czasowych niestacjonarnych,
sprowadzonych do stacjonarnych poprzez wyeliminowanie
występującego trendu. Jego budowa oparta jest na zjawisku
autokorelacji, czyli na korelacji wartości zmiennej prognozowanej
z wartościami tej samej zmiennej opóźnionymi w czasie.

 
Etapy:
-Uzupełnienie Yt-1, Yt-2, Yt-3 oraz Yt-4, poprzez odpowiednie

wklejenie danych Yt (o odpowiednią ilość wierszy niżej);

-Wyznaczenie funkcji regresji za pomocą Analizy danych – Regresja;
- Oszacowanie parametrów, eliminacja nieistotnych zmiennych za

pomocą metody regresji krokowej do tyłu;

-Wyznaczenie prognozy.

Model autoregresji

Za jego pomocą modeluje się szeregi stacjonarne, w
których występują wahania losowe wokół średniej, lub
niestacjonarne – sprowadzone do stacjonarnych.

 
Etapy:
-Ustalamy, czy model jest multiplikatywny, czy addytywny na

postawie wykresu badanej zmiennej, ocena stacjonarności.

- Wprowadzamy parametry do modelu (t, t^2, S1, S2, S3, S4,

S5, S6, S7, S8 S9, S10, S11, Yt-1, Yt-2)

-Wyznaczenie funkcji regresji za pomocą Analizy danych –

Regresja;

-Oszacowanie parametrów, eliminacja nieistotnych zmiennych

za pomocą metody regresji krokowej do tyłu;

-Wyznaczenie prognozy.

Trafność wyznaczonych prognoz zostanie oceniona i
porównana na podstawie obliczonych błędów dla
poszczególnych metod



MAE - Średnia Bezwzględnej Wartości Błędów Prognoz;



MAPE - Średnia Bezwzględnej Wartości Błędów
Procentowych Prognoz;



MSE - Średni Kwadratowy Błąd Prognozy;



RMSE - Odchylenie Standardowe Błędów Prognoz .

Zostanie także policzony test Durbina-Watsona
oraz
test serii dla dużych prób (test Walda – Wolfowitza) oparty na

statystyce Z.

Prognoza na podstawie metody wskaźników
sezonowości

Błędy prognozy:
MAE = 719,32 Przeciętne absolutne odchylenie wartości

zmiennej od wartości prognozy wynosi 719,32. Model myli
się o 719,32 jednostek.

MAPE = 6,49 Przeciętne absolutne procentowe odchylenie

wartości zmiennej od wartości prognozy wynosi 6,49 %.
Jest to wynik dość dobry, wskazujący na wysoką
poprawność prognozy.

MSE = 882571,07 Średnia suma kwadratów odchyleń

zmiennej od wartości prognozowanych jest równa
882571,07. Nominalnie wartość ta jest wysoka, oznacza to
więc, że wyznaczona prognoza jest mało dokładna

RMSE = 939,45

Test Durbina Watsona
d = 2,12
d1 = 1,69
d2 = 1,72
d3 = 2,27
d4 =2,31

Na podstawie przeprowadzonego testu Durbina Watsona
możemy stwierdzić, że w resztach brak autokorelacji,
ponieważ statystyka d znajduje się w przedziale d2, a d3.

Test serii
Z = 1,205;
Z* = 1, 979.

Po przeprowadzeniu testu serii dla dużych prób, można
stwierdzić losowość rozkładu składnika losowego,
ponieważ wartość Z < Z*

6 000

8 000

10 000

12 000

14 000

16 000

18 000

20 000

Yt

Yt

^

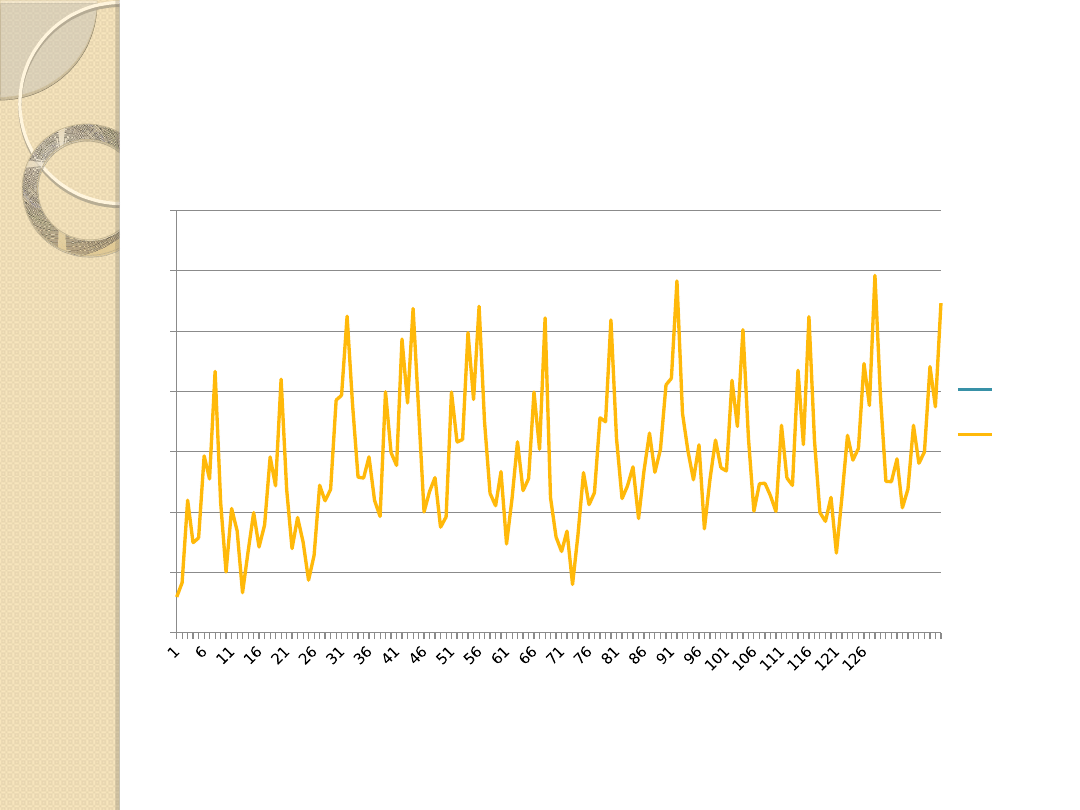
Wykres 3. Wartości rzeczywiste oraz prognoza na postawie wskaźników sezonowości na 2016 rok

.

Źródło: Opracowanie własne.

Prognoza na podstawie modelu autoregresji

Błędy prognozy:
MAE = 833,19 Przeciętne absolutne odchylenie wartości

zmiennej od wartości prognozy wynosi 833,19. Model myli się
o 833,19 jednostek.

MAPE = 7,52 Przeciętne absolutne odchylenie wartości

zmiennej od wartości prognozy wynosi 7,52 %. Jest to wartość
korzystna z punktu widzenia dokładności prognozy

MSE = 1208074,75 Średnia suma kwadratów odchyleń

zmiennej od wartości prognozowanych jest równa.
1208074,75. Nominalnie wartość ta jest wysoka, oznacza to
więc, że wyznaczona prognoza jest mało dokładna

RMSE = 1 099,12

Test Durbina Watsona
d = 2,3
d

l

= 1,5,

d

u

= 1,9

W takim przypadku zachodzi nierówność: 4-d

u

<d<4-d

l

czyli

test nie  rozstrzyga kwestii autokorelacji gdyż jesteśmy w
tzw. obszarze niekonkluzywności,. Nie możemy podjąć
jednoznacznej decyzji.

Test serii
 Z = 1,712; Z* = 1,979

Po przeprowadzeniu testu serii dla dużych prób można
stwierdzić losowość rozkładu składnika losowego,
ponieważ |Z|<Z*

Współczynnik determinacji R

2

wynosi 0,793567, co

oznacza, iż 79% zmienności zmiennej zależnej (objaśnianej)
jest wyjaśniany za pomocą zmiennej niezależnej.

1

6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91 96

10

1

10

6

11

1

11

6

12

1

12

6

6 000

8 000

10 000

12 000

14 000

16 000

18 000

20 000

Yt
Yt^

Wykres 3. Wartości rzeczywiste oraz prognoza na postawie modelu autoregresji na 2016 rok

.

Źródło: Opracowanie własne.

Prognoza na podstawie
metody ARIMA

Błędy prognozy: 

MAE =1545,37

Przeciętne absolutne odchylenie wartości zmiennej od wartości
prognozy wynosi 1545,37. Model myli się średnio o 1545,37
jednostek.

MAPE = 13,46

Przeciętne absolutne procentowe odchylenie wartości zmiennej od
wartości prognozy wynosi 13,46 %. Jest to wynik dość dobry.

MSE = 3966715,25

Średnia suma kwadratów odchyleń zmiennej od wartości
prognozowanych jest równa. 3966715,25. Nominalnie wartość ta
jest wysoka, oznacza to więc, że wyznaczona prognoza jest mało
dokładna

RMSE = 1991,66

Test Durbina Watsona
d = 2,13;
d1 = 1,66;
d2 = 1,76;
d3 = 2,24;
d4=2,34.

Na podstawie przeprowadzonego testu można stwierdzić,
że w resztach brak autokorelacji, ponieważ statystyka d
znajduje się w przedziale d2, a d3.

Test serii
Z = 1,205;
Z* = 0,8019
Z < Z*

Na podstawie testu serii dla dużych prób można stwierdzić
losowość rozkładu składnika losowego, ponieważ wartość Z
< Z*.

I 2

00

5

VI

2

00

5

XI

20

05

IV

2

00

6

IX

20

06

II 2

00

7

VI

I 2

00

7

XII

2

00

7

V

20

08

X

20

08

III

20

09

VI

II 2

00

9
I 2

01

0

VI

2

01

0

XI

20

10
IV

2

01

1

IX

20

11

II 2

01

2

VI

I 2

01

2

XII

2

01

2

V

20

13

X

20

13

III

20

14

VI

II 2

01

4
I 2

01

5

VI

2

01

5

XI

20

15

IV

2

01

6

IX

20

16

6 000

8 000

10 000

12 000

14 000

16 000

YT
Yt^

Wykres 4. Wartości rzeczywiste oraz prognoza na 2016 rok
na podstawie modelu ARIMA

Źródło: Opracowanie własne

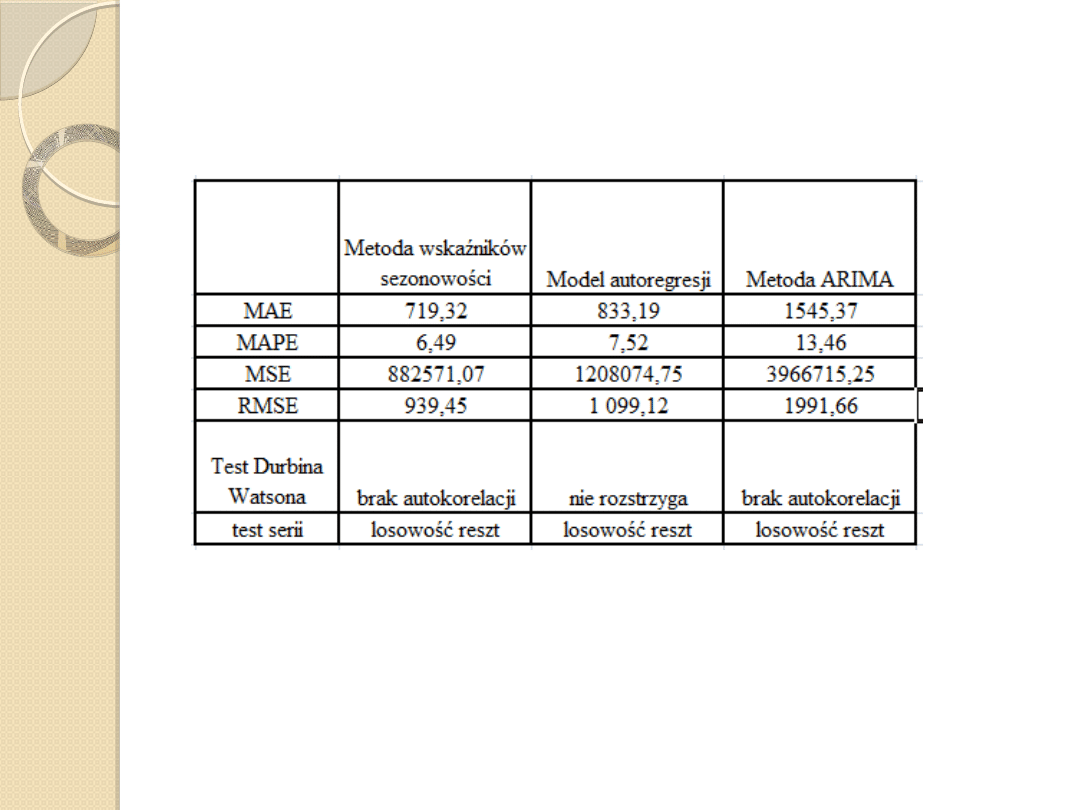
Ocena dopuszczalności i realności prognoz

Tab.1. Porównanie błędów prognoz oraz testu serii i testu Durbina Watsona dla
zastosowanych metod

Powyższa analiza modelu pozwala stwierdzić , że jest to model

poprawny i może posłużyć do zbudowania prognozy na kolejny rok.
Można zaobserwować dokonując oceny wzrokowej załączonych wyżej
wykresów, że model dobrze odzwierciedla zjawisko kształtowania się
ilości mieszkań oddanych do użytkowania w przeszłości można też
przypuszczać, że dobrze będzie opisywał zjawisko w przyszłości.