Całka krzywoliniowa skierowana

(całka krzywoliniowa funkcji wektorowej)

Niech K – krzywa regularna o początku A i końcu B, zawarta w 3

R

W – pole wektorowe,

3

W : K → R

3

W : K ∋ ( x, y, z) → [ P( x, y, z), Q( x, y, z), R( x, y, z)] ∈ R

W = [ P, Q, R]

z

B=An

K

Ai

W(M i)

Ai-1

A3

y

A M

2

3

W(M )

3

M

A1 2

W(M )

1

W(M )

2

M1

x

A=A0

Wtedy

•

dzielimy krzywą K na n krzywych punktami: A = A , A .

, ..

, A

, gdzie

0

1

= B

n

A ( x , y , z ) dla i= 1,2 ,…,n i

i

i

i

 

 →

•

tworzymy wektory cięciw: A A

r

x

x

y

y

z

z

dla i = ,

1 ,

2 ..., n

i

i = ∆ i = [

i −

,

i

i −

,

i

i −

]

1

−

1

−

1

−

i 1

−

•

wybieramy po jednym punkcie M na każdej z krzywych cząstkowych A A i

i 1

−

,

i

M ∈ A A dla i= 1,2 ,…,n

i

i 1

−

i

•

wyznaczamy wektory W ( M ) = [ P( M ), Q( M ), R( M )] dla i= 1,2,…, n i

i

i

i

•

tworzymy sumę

n

n

σ

W M

ο r

P M

x

x

Q M

y

y

R M

z

z

,

n = ∑

(

)

i

∆ i =∑ ( )(

i

i −

)

i

+ (

)(

i

i −

)

i

+ (

)(

i

i −

)

1

−

1

−

i 1

−

i 1

=

i 1

=

gdzie „ ο” oznacza iloczyn skalarny wektorów.

Definicja

Jeśli przy n → ∞ i max ∆ r

istnieje granica limσ niezależna od sposobu

i  

 →0

n→∞

n

i= ,

1 ..., n

n→∞

podziału krzywej i od wyboru punktów Mi, to granicę tę nazywamy całką krzywoliniową skierowaną funkcji W wzdłuż krzywej K i oznaczamy

∫ Wdr = ∫ Pdx + Qdy + Rdz .

K

K

7

Uwagi

1) ∫ Wdr = −∫ Wdr

− K

K

 x = x( t)

2) Jeśli krzywa K

, K ⊂ OXY , jest zadana układem K : 

, gdzi

e t ∈[α , β ] , a na

 y = y( t)

krzywej K zadane jest płaskie pole wektorowe W o składowych [ P,Q], to wtedy podobnie definiujemy całkę krzywoliniową skierowaną i oznaczamy ją

∫ Wdr =∫ Pdx + ∫ Qdy .

K

K

K

3) Jeśli K = K ∪ ...

, gdzie K jest krzywą regularną dla i=1,…, n, 1

∪ Kn

i

to definiujemy

n

∫ Wdr =

: ∑ ∫ Wdr .

K

i=1 Ki

Twierdzenie (o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną) Niech K – krzywa regularna,

W – pole wektorowe ciągłe na krzywej K

, W ∈ C( K ).

Wtedy

∫ Pdx + Qdy + Rdz =

K

β

= ∫ [ P( x( t), y( t), z( t)) '

⋅ x ( t) + Q( x( t), y( t), z( t)) '

⋅ y ( t) + R( x( t), y( t), z( t)) '

⋅ z ( t)] dt.

α

Uwaga

Jeśli krzywa K jest płaska, to

β

∫ Pdx + Qdy = ∫[ P( x( t), y( t), z t())⋅ x' t() + Q( x t(), y t(), z( t))⋅ y' t()] dt .

K

α

Interpretacja fizyczna

Niech K – krzywa skierowana od A do B, W – pole sił na krzywej K.

Wtedy

∫ Wdr = praca siły W wykonana przy przemieszczaniu masy jednostkowej wzdłuż K

krzywej K od punktu A do B.

Przykład (*)

Obliczyć całkę ∫ xydx + xdy po krzywej K: 4 x 2 2 y 2

+

= 2 skierowanej ujemnie względem

K

swego wnętrza.

x 2

Zapiszmy równanie określające krzywą K w postaci równoważnej

+ y 2 = 1.

1

2

Jest to równanie elipsy.

8

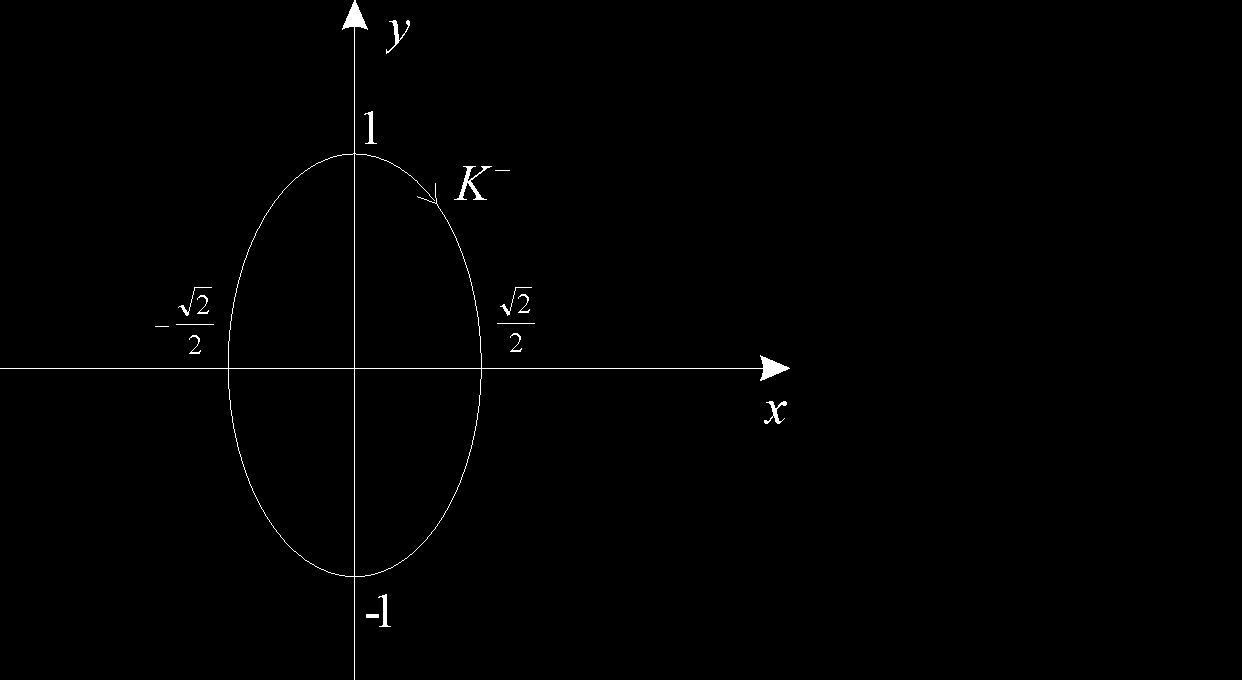
Parametryzacja tej elipsy



2

−

x =

cos t

K: 

2

, gdzie t ∈[ ,

0 2π ]

 y = sin t

jest niezgodna z kierunkiem krzywej. Zatem

2π 







∫

2

2

2

xydx + xdy = − ∫ xydx + xdy = − ∫ 

cos t ⋅ sin t ⋅  −



sin t +

cos t ⋅ cos t dt =

 2



2



2



K

− K

0 



π

π

1 2

2 2

1

2π

2 

1

2

 π

=

∫ 2

sin t ⋅ cos tdt −

∫

2

cos tdt =

3

sin t

−

t +

sin 2 t

π

2

2

6





= − 2

0

4

2

2

0

0

0

Definicja

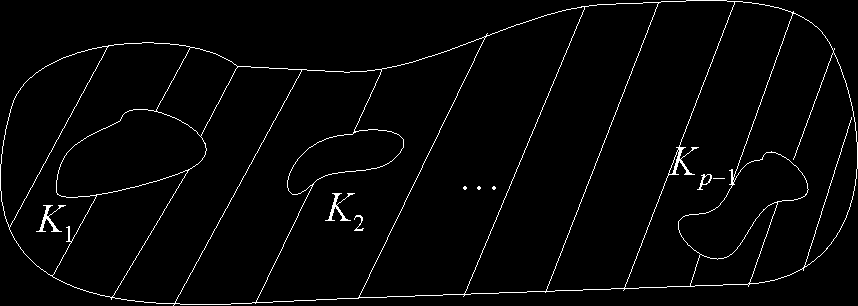
Obszar płaski ograniczony jedną krzywą (Jordana) nazywamy jednospójnym, a obszar ograniczony p nieprzecinającymi się krzywymi obszarem p-spójnym.

obszar jednospójny

obszar p-spójny

Umowa

Całkę krzywoliniową skierowaną po krzywej zamkniętej K oznaczamy też ∫ Pdx + Qdy .

K

9

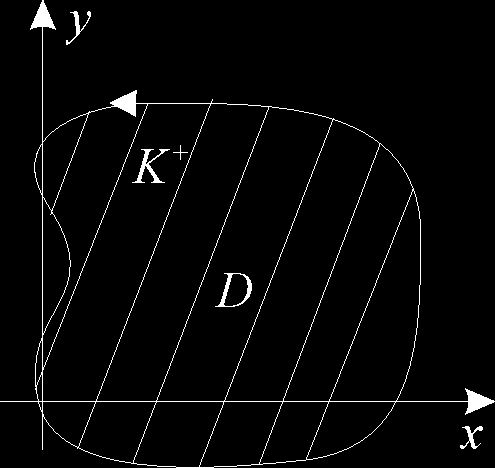
Twierdzenie Greena

Z: Niech K - krzywa płaska zamknięta zorientowana dodatnio i ograniczająca obszar jednospójny D,

P, Q - funkcje ciągłe mające ciągłe pochodne cząstkowe w obszarze D i na brzegu K.

 ∂ Q

∂ P



T: ∫ P( x, y) dx + Q( x, y) dy = ∫∫ 

−

 dxdy

 ∂

∂

+

x

y



K

D

Przykład (*) c.d.

K jest krzywą zorientowaną ujemnie, K = K − , (

∂ Q

Q x, y) = x ⇒

=

∂

1

x∂

P

P( x, y) = xy ⇒

= x

∂ y

i z twierdzenia Greena otrzymujemy

 ∂ Q ∂ P

∫ P( x, y) dx + Q( x, y) dy = − ∫ P( x, y) dx + Q( x, y) dy = − 

∫∫

−

 dxdy = −∫∫ (1− x) dxdy =...

 ∂ x

∂ y 

K

− K

D

D

Zastosujemy uogólnione współrzędne biegunowe

 x = ar cosϕ



∈[ ,

0 2 ).

 y = br sinϕ , gdzie a, b – stałe, r ≥ 0 , ϕ

π

Jakobian powyższego odwzorowania wynosi J = abr .

2

W naszym przypadku wybieramy a =

i b = 1 , aby otrzymać obszar D ograniczony 2

x 2

elipsą

+ y 2 = 1.Stąd

1

2

2

x =

r cosϕ

2

2π

1 



2

2

...= y = r sinϕ

= −



∫ dϕ∫ 1−



r cosϕ

rdr =



2

 2

0

0

r ∈[ ,

0 ]

1 ϕ ∈[ ,

0 2π ]

10

2π 

2π

1

1 





= − 2 

∫ 1

2

1

2

2

r

− 2 cosϕ ⋅ 1 3 

r

dϕ = = −



∫

−



cosϕ dϕ =

2

 2

2

 2

6



0

2

3

0 

0

0



2π

2π 





= − 2  1

2

2

2

2

 ϕ

−



sinϕ

 = = −

π −

⋅ 

0 = −

π

2  2

2 

6



0

6

0 

2

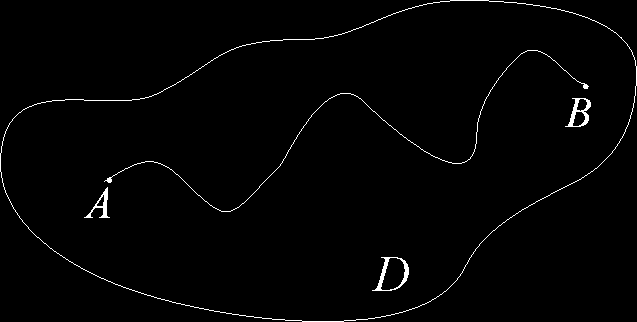
Twierdzenie (o niezależności całki krzywoliniowej od kształtu drogi całkowanej) Z: Niech D - obszar jednospójny

P, Q - funkcje ciągłe, mające ciągłe pochodne cząstkowe w obszarze D

AB - krzywa regularna , AB ⊂ D

∂ Q ∂ P

T: ∂ =

⇔ ∫ Pdx + Qdy - nie zleży od kształtu krzywej AB a tylko od punktów A i B, x

∂ y

AB

B

t i wtedy oznaczamy ją ∫ Pdx + Qdy .

A

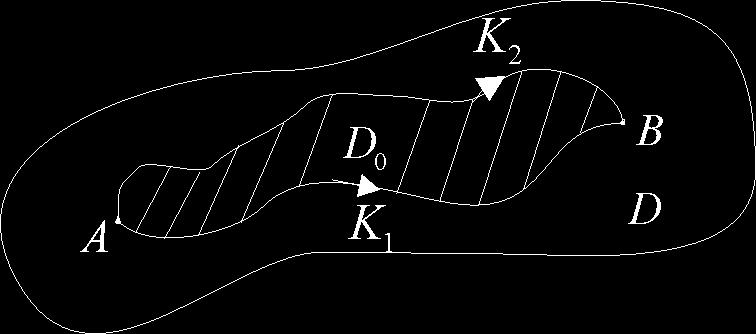
Dowód (⇒)

Niech K , K będą krzywymi regularnymi zawartymi w obszarze D, łączącymi punkty A i B, 1

2

i skierowanymi od punktu A do B.

Wtedy krzywa C = K

jest krzywą zamkniętą regularną, zorientowaną dodatnio,

1 ∪ −( K 2 )

C = C + . Oznaczmy przez D obszar jednospójny ograniczony przez krzywą C. Na podstawie 0

twierdzenia Greena mamy

 Q

∂

P

∂ 

∂ Q ∂

∫

P

Pdx + Qdy =



∫∫

−

 dxdy = 0 bo

−

= 0 , więc

 ∂

∂

∂ x ∂

+

x

y 

y

C

D 0

∫ Pdx + Qdy + ∫ Pdx + Qdy = 0

K 1

− K 2

∫ Pdx + Qdy − ∫ Pdx + Qdy = 0

K

K

1

2

∫ Pdx + Qdy = ∫ Pdx + Qdy

K

K

1

2

(⇐)

11

Aby udowodnić implikację (⇐) wystarczy wykazać jej kontrapozycję, czyli udowodnić implikację ∂ Q ∂ P

∂ ≠

⇒ ∫ Pdx + Qdy zależy od kształtu krzywej AB .

x

∂ y

AB

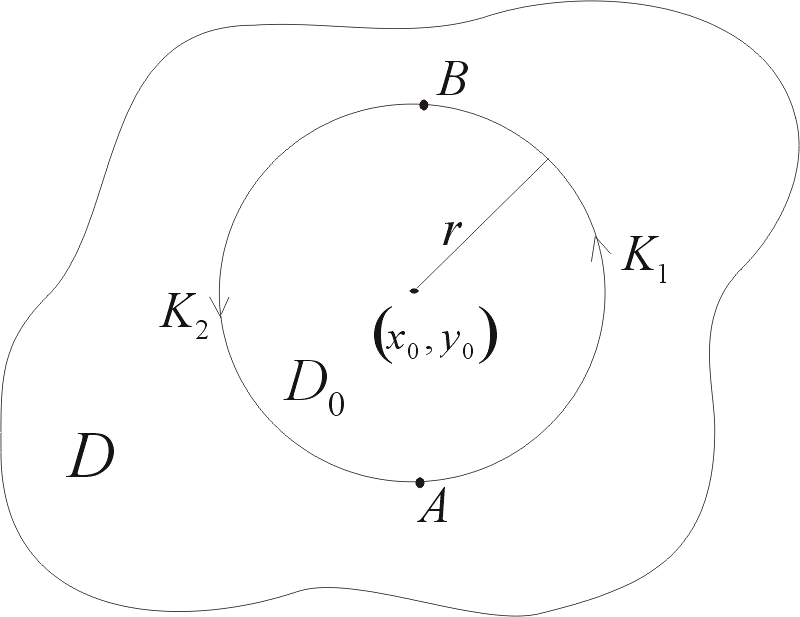
Bez straty ogólności możemy założyć, że

(

∂

∂

∃

Q

P

x , y ) ∈ D:

( x , y )− ( x , y 0

0

0

0

0

0

0 ) >

x

∂

y

∂

.

Zatem

∂

∂

∃

Q

P

r > 0:

( x, y)− ( x, y) > 0

x, y ∈ D

.

0 = K( x , y

, r

0

0

)

x

∂

y

∂

dla (

)

(

)

Niech C = K

będzie brzegiem koła D skierowanym dodatnio.

1 ∪ K 2

0

Wtedy na podstawie twierdzenia Greena mamy

 Q

∂

P

∂ 

∫ Pdx + Qdy = 

∫∫

−

 dxdy > 0.

 ∂

∂

+

x

y 

C

D 0

Stąd

∫ Pdx + Qdy + ∫ Pdx + Qdy > 0 , K

K

1

2

czyli

∫ Pdx + Qdy > ∫ Pdx + Qdy .

K

K

1

2

Zatem całka po krzywej łączącej punkty A i B zależy od kształtu tej krzywej.

Wniosek

Niech D - obszar jednospójny,

C – krzywa zamknięta regularna, C ⊂ D , P, Q - funkcje ciągłe mające ciągłe pochodne cząstkowe w D.

Wtedy

∂ Q ∂ P

∂ =

⇔ ∫ Pdx + Qdy = 0 .

x

∂ y

C

12