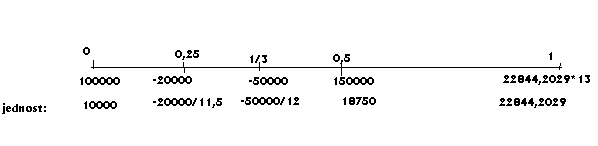
Egzamin dla Aktuariuszy z 6 grudnia 2003 r.
Matematyka Finansowa
Zadanie 1
i = 1
,
1 0,25 −1 - stopa kwartalna
100000 1
( + i)40 − Xs
= 60000 → X wyliczamy
40; i
OD( I ) = 40 X − 40000
j = 08
,
1
0,25 −1
40
é
60000
å
ù
j 60000 − ( k − ) 1
ê
ú
ë
û
1
=
40
OD( )
2 = k
g
z
bo
ory pl
acimy
08
,
1
25
OD( I ) + OD(2) ≈ 104102
Zadanie 2
TEORIA:
Met. Kapitałowa: wpłaty: 100000-20000-50000+150000=180000
Zysk=I=22844,2029*13-180000=116974,6377
2
I = i ⋅100000 − 20000 ⋅ 75
,
0
i − 50000 ⋅ ⋅ i + 150000 ⋅ 5
,
0 i → i wylicza y m
1
3
Metoda (time-weighted):
10000 ⋅
5
,
11
1 + j
=
0,25
100000
20000
1
( 0000 −
) ⋅12
11 5
,
1 + j =
1
10000 ⋅11 5
, − 20000
3
æ
20000
50000 ö
ç10000 −
−
÷ ⋅8
è
11 5
,
12
ø
1 + j
=
0,5
æ
20000 ö
ç10000 −
÷ ⋅12 − 50000
è
11 5
,
ø
,
22844 2029 ⋅13
1 + j =
1
æ
20000
50000 ö
ç10000 −
−
÷ ⋅8 +150000
è
5
,
11
12
ø
1
( + i ) = 1
( + j
) 1
( + j ) 1
( + j ) 1
( + j ) = 3
,
1 → i = 3
,
0
2
0,25
1
0,5
1
2
3
ODP = i − i ≈ 62 %
3
,
1
2
Zadanie 3
Odsetki zapłacone: jk
1
−
−2
1
n
n
X 1
( + i)
+ X 1
( + i)
+ ... + X = 1 → tyl ew f undusz → X =
sn
Ia
1. X ( s − kX
;
1
−
=
k )
( ) k i
sn
(
&
& −
Is) =
1
( + ) =
n
( Ia)
s
n
i n
n
n
i
2.
(
&
&
− ( − )
1
−
Is)
s
k
s
k
k −1
k
−1 =
=
k
i
i
Z 1 i 2 wynika:
i( Is) k− i;1
sn
Z tego odpowiedź A.
Zadanie 4
ODP = a∞ + 2 va∞ + 3 2
v a∞ + ... = a 1
(
∞
+ 2 v + 3 2
v + ...)
I = 1 + v
2 + v
3 2 + ...
Iv = v + v
2 2 + v
3 3 + ...
a
2
∞ + 1
I 1
( − v) = 1 + v + v + ... = a∞ + 1 → I = 1− v v
+1
a + 1
v
1 −
ODP =
∞
v
v
a∞
=
=
≈ 8820
1 − v
1 − v 1 − v
1
( − v)3
Zadanie 5
Po przekształceniach:
( m + )
1 2 2
i + (2 2
m + 5 m − )
2
2
i + m + 3 m + 1 = 0
.
1 m ≠ − b
1
o wtedy l
iniowe
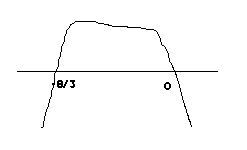
∆ > 0 → ∆ = -15m2 − 40 m
æ 8 ö
m ∈ ç −
0
; ÷ \ {− }
1
è 3 ø
− 2(2 2
m + 5 m − 2)
−16 − 2 71
2 71 −16
i + i =
< 5
,
1 → ∆ = 4 ⋅ 71 → i =
, i =
1
2
2
1
2
2( m + )
1
14
14
æ
ö
8 −16 − 2 71
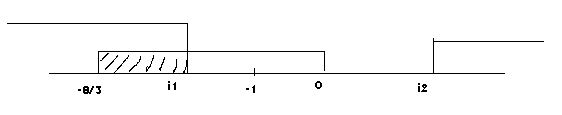
z tych dwóch wynika, że: m ∈ çç− ;
÷÷
è 3
14
ø
Widać, że nic nie pasuje i dalej nie trzeba ...
Zadanie 6
r = 2
1
r = 2
r ,..., r
= 26
2
29
39
...
r
= 26
40
...
r = 24
41
r = 38
...
19
r ,..., r = 38
...
20
26
r = 34
r = 4
27
51
r = 30
28
2 v + 4 v 2 + ... + 3 v 19
8
+ 3 (
8 v 20 + ... + v 26 ) + 34 v 27 + 30 v 28 + 26( v 29 + ... + v 39 ) + 26 v 40 + 24 v 41 + .. + 4 v 51 =
= 2 Ia + 3 v 19
8
a + 34 v 27 + 30 v 28 + 26 v 28 a + v 39 28
2
19
7
11
[ a − Ia
12
12 ] = N
N =
N
8 %
0 B → B =
≈ 213 8
, 1
8
,
0
Zadanie 7
ì
æ 1 ö7
ï150000 = R a
R a
1
+ ç
÷
ï
7;0,05
è ,
1 05 ø
1
7;0 1
,
ïï
æ 1 ö4
í D )
3
(
= R a
R a
1
+ ç
÷
ï
4;0,05
è ,
1 05 ø
1
7;0 1
,
ï D )
3
(
+ 75000 =
ï
R a
2
20;0 1
, 5
ïî
150000
R =
1
7
æ 1 ö
a
+ ç
÷ a
7;0,05
7;0 1
,
è 0
,
1 5 ø
4
æ
ö
æ 1
ç
ö
÷
R a
+ ç
÷ a
+ 75000
1
4;0,05
ç
è 0
,
1 5
7;0 1
, ÷
è
ø
ø
R =
≈ 31553
2
a 20;0 1,5
Zadanie 8
(i)
NIE bo:
2 ∂
L = i
[1(+ i −1) + 1(+ i −2) +...+ 1(+ i − n)]= i 2[− v 2 − v 3
2
− ... − nvn+1]= − vIa i 2 =
i
n
∂
æ
1
1
ö
n
n
= v ç −
+ v÷ ≠ P
è i 2
i 2 v n
i ø
(ii)
NIE bo:
∂
L =
[1(+ i)− k + 1(+ i)−2 k +..].= − k[ k 1+
v
+ 2 2 k 1+
v
+ .. ].
∂ i
k 1
+
2 k 1
I = v
+ 2 v + + ...
k
2 k 1
+
3 k 1
Iv = v
+ 2 v + + ...
k 1
+
k 1
+
+
v
v +
k
k 1
2 k 1
I 1
( − v ) = v
+ v
+ ... =
→ I =
k
k
2
1 − v
1
( − v )
k
k
k
k +
k +
L = − k (
[
1
2
1
k
v
− k − v v v
− kv
1 + i) − ]
1
(
)
1
=
=
< 0
1
( − k
v )2
1
( − k
v )2
1 − k
v
k
P =
v
kv
k 1
( + i) k 1
−
=
>
0 c
zyl
i NIE
1 − k
v
1 − k
v
(iii)
TAK bo:
∂ ì1
2
tδ ü
P =
í e ý = etδ =
x
x
x
P b
o e = 1 +
+
+ ...
∂ t îδ
þ
!
1
!
2
Zadanie 9
1
( 20 − 9 )
5
p
= 0
,
9 9 → p = 3
,
0 9996
1
,
1
2
p ⋅ 49 + 2 p 1
( − p)
ODP :
≈ 8
,
6 7
1
,
1 2
Zadanie 10
t
e = x
ò 1 = t = ln x =
dx
x
x
t
e
t
ò 1 1 = ò 1 − 2 = ln −ln 1(+ 2 ) = −ln 1(+ 2 t) 1 + 2 e
1 + 2 x x
x
1 + 2 x
dt = 1 dx
x
2 t
e
= x
ò 2 = 2 t = ln x =
t
x
x
t
e
2 t
ò 2 1 = ò 1 − 3 = ln −ln 1(+3 ) = 2 − ln 1(+ 3 2 ) 1 + 3 e
1 + 3 x 2 x
x
1 + 3 x
dt = 1 dx
2 x
2
4
3
1 2 e
1 3 e
3
6
2
4
( + )( + )
ò δ
t = 9 − ln 1
( + 2 e ) 1
( + 3 e ) − 6 + ln 1
( + 2 e ) 1
( + 3 e ) = 3 + ln
2
1
( +
3
2 e ) 1
( +
6
3 e )
(
A )
2 = 1
A )
3
(
= exp(ò3δ
)
t
= exp( )
3 exp(ln...)
2
1
( + 2 2
e ) 1
( + 3 4
e )
ODP = exp( )
3
−1 ≈
%
7
,
4
1
( + 2 3
e ) 1
( + 3 6
e )
Wyszukiwarka
Podobne podstrony:
Egzamin 2003.12.06, rozwiazania zadań aktuarialnych matematyka finansowa
mat fiz 2003 12 06 id 282350 Nieznany
2003 12 06 pra
2003.12.06 prawdopodobie stwo i statystyka
2003.01.25 matematyka finansowa
2003 12 06 prawdopodobie stwo i statystykaid 21710
2003 05 17 matematyka finansowaid 21697
2010.12.13 matematyka finansowa
1 2009.04.06 matematyka finansowa
2008.10.06 matematyka finansowa
2000.12.09 matematyka finansowa
2008.12.15 matematyka finansowa
2008 12 15 matematyka finansowaid 26464
2005 12 05 matematyka finansowaid 25347
2003 10 11 matematyka finansowaid 21704
2003 12 06
1 2009 04 06 matematyka finansowaid 8923
2007 12 03 matematyka finansowaid 25661
mat fiz 2003 12 06 id 282350 Nieznany
więcej podobnych podstron