ANALIZA STANU NAPRĘŻEŃ Jednokierunkowy stan naprężeń

σ_α=p*cosα τ_α=p*sinα

σ_α=σcos²α τ_α=σcosαsinα=0,5σsin2α

ŚCINANIE

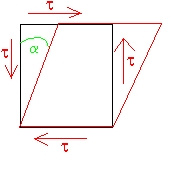
γ - kąt odkształcenia postaciowego

Prawo Houke'a przy czystym ścinaniu: τ=G*γ

G-moduł Kirhoffa (moduł sprężystości postaciowej) Dla stali G=8*10⁴ MPa

ŚCINANIE TECHNOLOGICZNE

k_t - naprężenie dopuszczalne na zginanie

k_t ≈ 0,6*k_r

R_t - wytrzymałość na ścinanie

warunek, aby nastąpiło ścięcie:

GEOMETRIA FIGURY PŁASKIEJ

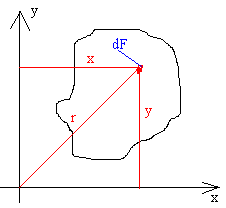
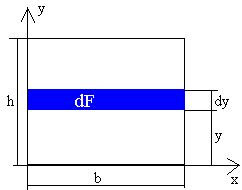
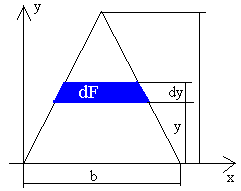
twierdzenie Steinera:

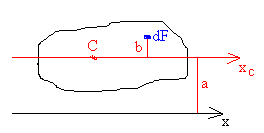
Moment odśrodkowy (dewiacji , zboczenia ):

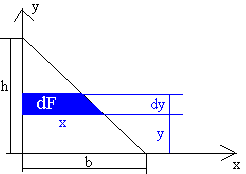
Osie główne centralne - są dwie osie względem których moment odśrodkowy jest równy zero

Dla okręgu

Dla trójkąta

Dla prostokąta

SKRĘCANIE

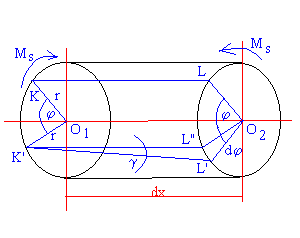
φ - kąt skręcenia wału γ - kąt odkształcenia postaciowego

- warunek wytrzymałości

φ_dop=0,2⁰-2⁰ na 1 m długości wału

WAŁ STATYCZNIE NIE WYZNACZALNY

I część statyczna Σ_Mix=0

M_B-M+M_A=0 M=M_A+M_B Jednokrotnie statycznie niewyznaczalne

II część teoretyczna ϕ_c=0

III część fizyczna

ZGINANIE

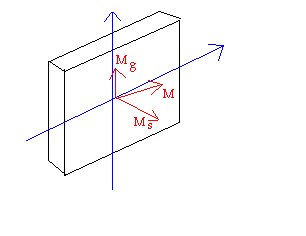
Zginanie czyste

Zginanie ukośne

Zginanie proste

UOGÓLNIONE PRAWO HOUKE'A

zależność między 3 stałymi materiałowymi

ODKSZTAŁCENIA BELKI ZGINANEJ

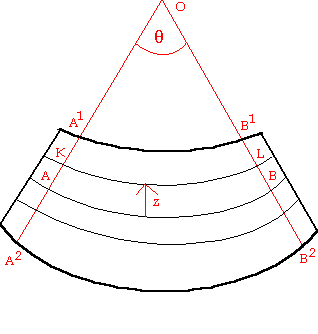
Skrócenie włókna

Warstwa obojętna

Wydłużenie włókna

Naprężenia przy zginaniu

1)

skoro S_y=0 to punkt ciężkości leży na osi y, która jest osią obojętną

2)

wskaźnik wytrzymałości przekroju na zginanie

3)

- jeżeli moment odśrodkowy jest równy zero to osie z i y są głównymi centralnymi

WYBOCZENIE

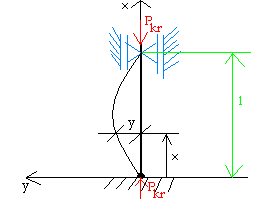
warunki podparcia

dla n=1

l_w - długość wyboczeniowa

S - smukłość

minimalny promień bezwładności

- wzór Eulera

dla S > S_gr

wyprowadzenie wzoru na prostą Tetmajera-Jasińskiego

nasza prosta będzie miała postać:

prosta ta przechodzi przez punkty

- dla S<S_gr

n_w>1 PN-80/B-03200

ODKSZTAŁCENIA BELKI

- równanie linii ugięcia belki

- równanie linii kąta ugięcia belki

dla małych α

aby wyznaczyć stałe całkowania należy uwzględnić warunki podparcia

a w przypadku belek dwuprzedziałowych dodatkowo warunki zszycia

ZGINANIE MIMOŚRODOWE

METODY ENERGETYCZNE

- rozciąganie

- skręcanie

- zginanie

- wzór na energię

sprężystą

układ Clapeyrona

- materiał idealnie sprężysty

- układ, w którym można stosować metodę superpozycji

TWIERDZENIE CASTIGLIANO

pochodna cząstkowa energii sprężystej po sile uogólnionej równa się przesunięciu uogólnionemu

PODSTAWOWE POJĘCIA

-definicja naprężenia

σ-naprężenie normalne

τ-naprężenie styczne

Zasada de Saint-Venanta 1,5 d

1.Związki statyki(związki równowagi)

2.Związki geometryczne

Δl=l₁-l wydłużenie bezwzględne

3.Związki fizyczne

Prawo Houke'a σ=Ε*ε E- moduł sprężystości wzdłużnej (moduł Younga)(pierwsza stała materiałowa) dla stali E=2,1*10⁵­­ MPa

Wyprow:

ε'=-υ*ε υ- liczba Poissona(druga stała materiałowa)

0≤ υ ≤0,5 υ=0 korek υ=0,3 stal υ=0.5 guma

R_m - wytrzymałość materiału na rozciąganie

R_0,05 -umowna granica sprężystości

R_0,2 -umowna granica plastyczności (odkształcenie trwałe wynosi 0,2%)

Warunek wytrzymałościowy σ≤σ_dop

n - współczynnik bezpieczeństwa n>1

dla materiałów plastycznych

k_c - naprężenia dopuszczalne przy ściskaniu

k_r=k_c dla stali k_r>k_c dla żeliwa

Zagadnienia statyczne wyznaczalne i niewyznaczalne

Metoda superpozycji:

-do przypadków gdzie występuje sprężystość

-nie ma zmiany charakteru sił

WYTRZYMAŁOŚĆ ZŁOŻONA

1)hipoteza największych naprężeń normalnych σ_max

2)hipoteza największego odkształcenia względnego ε_max (dla materiałów kruchych)

3)hipoteza największych naprężeń stycznych (Coulomba)

układ przestrzenny:

- stan obciążenia niebezpiecznego

4)hipoteza energetyczna (hipoteza energii odkształcenia postaciowego)

L=L_b+L_p L_b - energia odkształcenia objętościowego

L_p - energia związana ze zmianą postaci (energia postaciowa)

Naprężenia główne uważa się za niebezpieczne

hipoteza τ_max

hipoteza Hubera:

KOŁO MOHRA

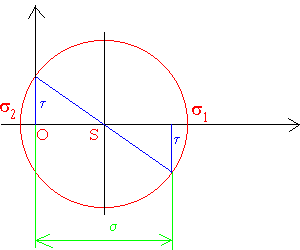
hipoteza τ_max:

dla hipotezy Huberta

gdy
to

Twierdzenie Menabrei (służy do wyznaczania wielkości statycznie nie wyznaczalnych)

Jeżeli mamy n równań i m reakcji, to n reakcji wyznaczamy w funkcji pozostałych reakcji statycznie niewyznaczalnych

Następnie zapisujemy równanie momentów w danym przedziale i różniczkujemy to równanie względem reakcji statycznie niewyznaczalnej

Wzór Maxwella-Mohra

METODA CLEBSCHA

- równanie momentów liczymy tylko od jednej strony belki zaznaczając koniec przedziału pionową kreską i dopisując kolejne wyrażenia bądź ( jeżeli następuje zmiana obciążenia ciągłego ) odejmując moment pochodzący od obciążenia ciągłego, , należy również pamiętać o „zerowym” ramieniu momentu skupionego; kolejnymi krokami jest scałkowanie powyższego równania i uwzględnienie warunków podparcia

-warunek sztywności

EI - sztywność belki na zginanie

---