UKŁADY O JEDNYM STOPNIU SWOBODY

1.Równanie ruchu

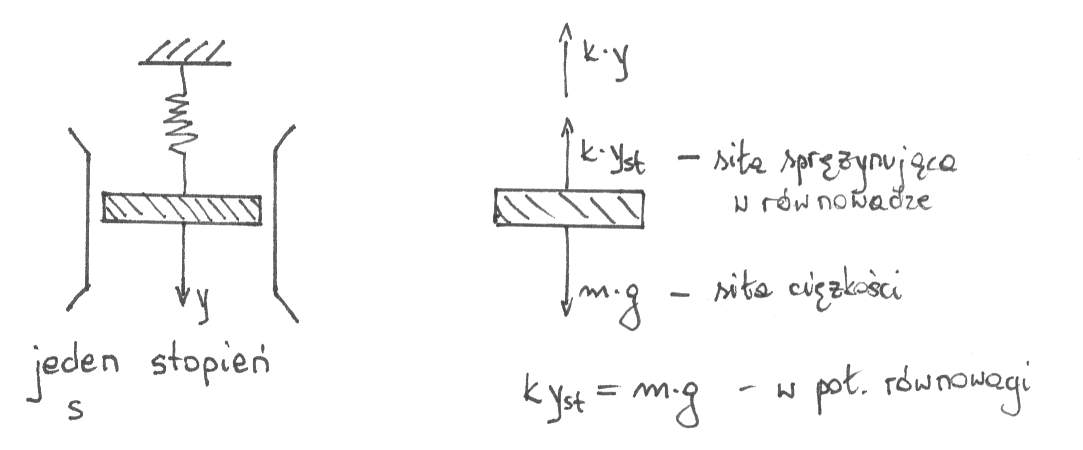
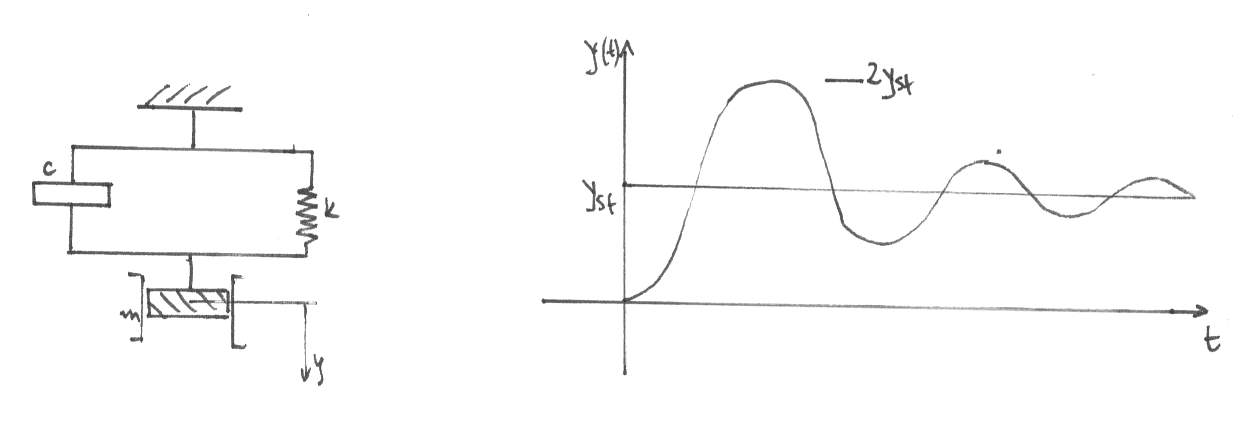
Najprostszy ideowy model układu o jednym stopniu swobody jest przedstawiony na rys.5-10. Masa m jest połączona z nieruchomą ostoją za pomocą więzi sprężystej o sztywności k oraz tłumika wiskotycznego o parametrze c .

Układ jest obciążony siłą wzbudzającą P(t), a wychylenie masy z położenia równowagi statycznej opisuje współrzędna uogólniona q(t) . Bilans energetyczny układu daje rezultaty :

E_k=
² E_p=
^2
2 L=Pq

Po wykorzystaniu równań Lagrange`a otrzymujemy równanie ruchu

(5.26)

Równanie to zgodnie z zasadą d`Alamberta wyraża warunek równowagi sił działających na rozważaną masę w czasie ruchu.

2.Zagadnienia własne. Drgania swobodne.

Rozwiązaniem zagadnienia własnego nazywamy w dynamice ustalenie okoliczności , w których równanie ruchu pozbawione składników reprezentujących siłę wzbudzającą i opory ruchu może mieć niezerowe rozwiązanie .Poszukiwana jest więc całka równania

Podstawiając q=e
otrzymamy równanie charakterystyczne
²+ k = 0 , którego pierwiastkami są
₁=
,
₂=
przy czym
,
²=k/m.

Charakter pierwiastków wskazuje na to , że całka ogólna równania ma postać

_ssin
t + q_ccos
t (*)

przy czym q_s , q_c są stałymi dowolnymi. Stacjonarny harmoniczny proces opisany powyższą funkcją nazywamy drganiami własnymi . Wielkość

jest częstością kołową drgań własnych. Jest ona indywidualna cechą rozważanego obiektu i nie zależy od czynników zewnętrznych . Drgania własne nie są procesem fizycznym , opisują one pewną dyspozycje ustroju.

Drganiami swobodnymi nazywamy proces fizyczny spowodowany wyłącznie początkowym zaburzeniem stanu równowagi , a więc nałożeniem warunków początkowych q(0) = q_o ,
_o .

W przypadku pomijalnie małego tłumienia całka ogólna równania ruchu ma postać (*) . Uwzględniając warunki początkowe : q(0) = q_c = q_o ,
q_s =
_o

Otrzymujemy:

q_c = q_{o ,} q_s =

Drgania swobodne układu tłumionego opisuje równanie :

(**)

Po podstawieniu q = e
^t otrzymujemy równanie charakterystyczne :

m
²+

Jeśli
< c <
, to pierwiastkami tego równania są

₁=
`
<sub>2</sub>=
`

Przy czym

`=
² (****)

Charakter pierwiastków wskazuje na to , że całka ogólna równania (**) ma postać:

q(t) = e
(q_s sin
`t + q<sub>c</sub>cos
`t) (***)

Wykorzystując jak poprzednio warunki początkowe , otrzymujemy :

q_c=q_o

q_s =

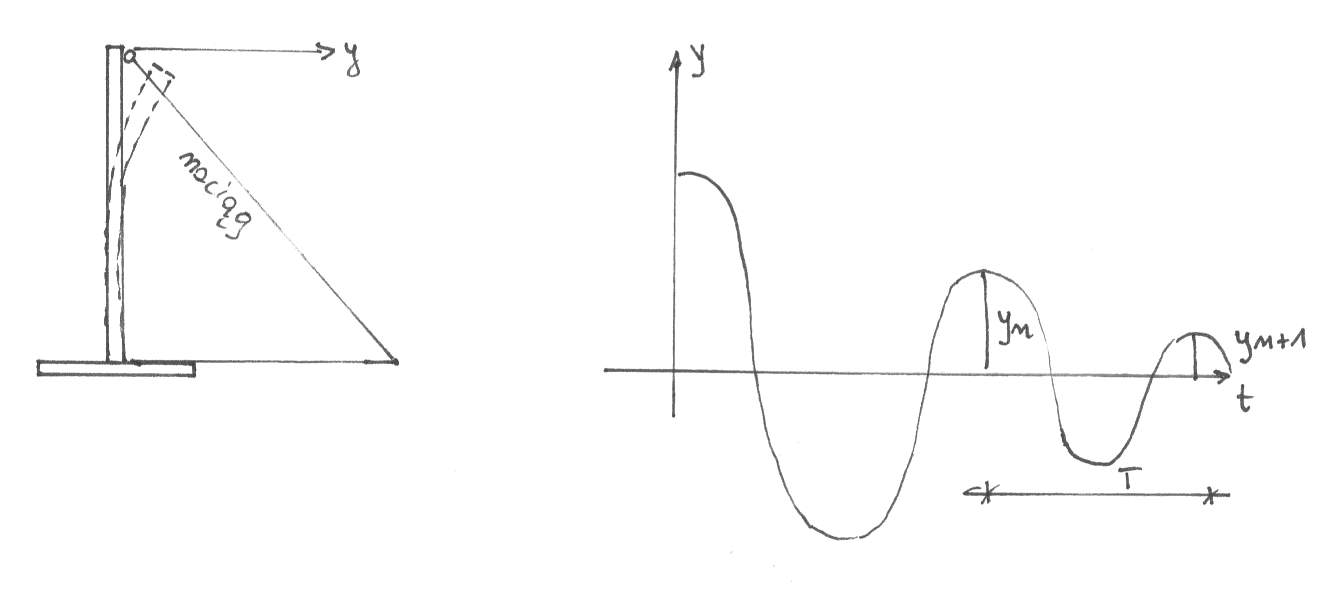
Ruch opisany funkcją (***) jest quasi-harmonicznym ruchem zanikającym , modulowanym funkcją wykładniczą
. Wykres ruchu jest poglądowo przedstawiony na rysunku 2 . Częstość kołowa tego ruchu ,
<
, jest określona wzorem (****), a quasi okres drgań tłumionych wynosi :

T`
>T

Rozwiązanie ma przebieg oscylacyjny , gdy bezwymiarowy parametr
, zwany liczbą tłumienia ,jest zawarty w przedziale
<1 . W przypadku
>1 ruch zanika w sposób aperiodyczny. Tłumienie określone liczbą
= 1 nazywamy tłumieniem krytycznym . W konstrukcjach budowlanych liczba tłumienia jest na ogół ułamkiem znacznie mniejszym od jedności.

Liczbę tłumienia można wyznaczyć doświadczalnie badając stosunek wychylenia
do wychylenia

q(t + T`) =
q(t). Wielkość bezwymiarową

nazywamy logarytmicznym dekrementem tłumienia. Z tego wzoru wynika , że

,

przy czym relacja przybliżona jest słuszna , gdy
<<2
. W przypadku małego tłumienia wygodnie jest korzystać ze wzoru

gdzie n jest liczbą naturalną większą od jedności.

Do opisu tłumienia używa się również bezwymiarowego współczynnika tłumienia

który podobnie jak parametry
i
, jest indywidualna cechą obiektu .

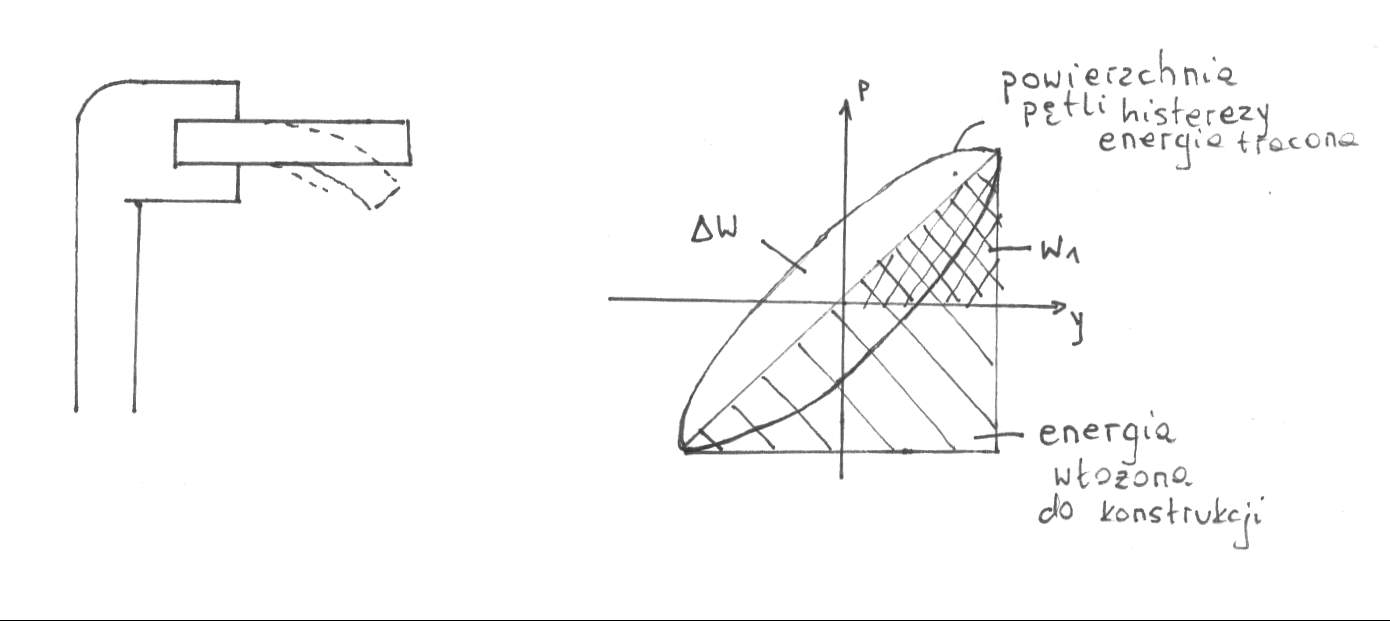
3.Warianty modelu tłumienia . Wytężenie konstrukcji.

Stan przemieszczenia konstrukcji odkształcalnej stanowi podstawę do określenia stanu jej wytężenia , jeśli znane są związki fizyczne między tymi materiałami. Reakcja więzi odkształcalnej zgodnie z zasadą d`Alemberta powinna być równa obciążeniu kinematycznemu , złożonemu z siły wzbudzającej , siły bezwładności i innych sił o charakterze wewnętrznym w stosunku do tej więzi . Definicja obciążenia kinematycznego nie jest oczywista , konstrukcje budowlane bowiem wykazują właściwości tłumiące , nie zawierając na ogół w sposób jawny tłumików służących do rozpraszania energii . W tej sytuacji możliwe są różne warianty modelu tłumienia i definicji wytężenia , odpowiadające ogólnie przyjętemu założeniu o wiskotycznym charakterze oporów ruchu . Załóżmy , że więz odkształcalna jest idealnie sprężysta. W tym przypadku obciążenie kinematyczne wyrazimy formułą :

Q(t) = kq =

w której opory ruchu zostały zakwalifikowane do grupy sił zewnętrznych i skojarzone z siłami bezwładności . Można przyjąć, że opory te są proporcjonalne do pędu masy , a więc że

c =
m

gdzie
jest wymiarowym parametrem tłumienia masowego , mierzonym w s^-1 . Zgodnie z tm założeniem otrzymamy bezwymiarowy współczynnik tłumienia :

Załóżmy z kolei , że opory ruchu mają charakter wyłącznie wewnętrzny (materiałowy). W tym przypadku obciążenie kinetyczne definiujemy wzorem :

Można tu przyjąć , że opory ruchu są proporcjonalne do prędkości reakcji sprężystej , a więc że
k

gdzie
jest wymiarowym parametrem tłumienia materiałowego , mierzonym w sekundach (czas retardacji) , co odpowiada reologicznemu modelowi ciała Voigita-Kelvina . Bezwymiarowy współczynnik tłumienia w tym przypadku wynosi

Ułamek tłumienia krytycznego: ξ=Δ/2π

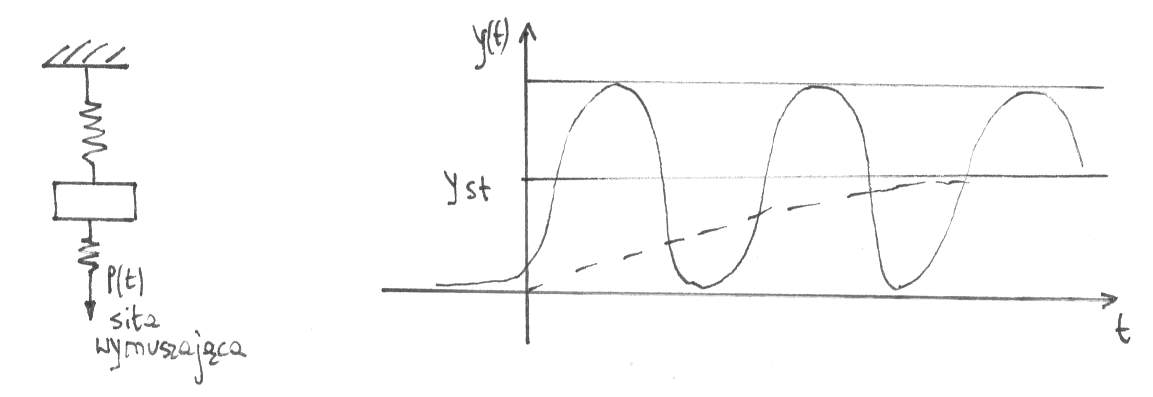
DRGANIA WYMUSZONE HARMONICZNE

Zakładamy ,że siła wzbudzająca w równaniu (5.26) jest harmoniczną funkcją czsu . Równanie ruchu przyjmuje postać

(5.52)

gdzie p jest częstością kołową wzbudzenia .Oznaczając jak poprzednio k/m=
,
,równanie to sprowadzimy do postaci

(5.53)

Całka ogólna równania jednorodnego jest funkcją zanikającą , skupimy uwagę na całce szczególnej , której będziemy poszukiwać w postaci funkcji harmonicznej

(5.54)

Równanie 5.53 po podstawieniu 5.54 powinno być spełnione tożsamościowo , niezależnie od czasu . Wynikają stąd dwa równana algebraiczne :

i obliczymy pierwiastki:

Przy kontroli naprężeń należy uwzględnić pewną właściwość materiałów , zwaną zmęczeniem .Liczne badania wykazały ,że w przypadku cyklicznie zmiennego stanu wytężenia podstawowa (statyczna) wytrzymałość materiału R_o zmniejsza się ze wzrostem liczby cykli i przy pewnej umownej dużej ich liczbie osiąga wartości R_z , zwaną wytrzymałością zmęczeniową (rys. 5-24).

Współczynnik

nazywamy podstawowym współczynnikiem zmęczeniowym dla cyklu symetrycznego.

W praktyce występują zwykle złożone stany wytężenia , statyczno dynamiczne , charakteryzujące się asymetrią cyklu (rys 5-25). W cyklu asymetrycznym możemy wyróżnić statyczny składnik naprężenia
oraz amplitudę symetrycznego składnika dynamicznego
. Warunek wytrzymałościowy z uwzględnieniem zmęczenia ma postać

(5-90)

Przekształcając relację 5-90 można uzyskać warunek dotyczący
. Ma on postać

gdzie

jest zredukowanym współczynnikiem zmęczeniowym uwzględniającym asymetrię cyklu.

Podstawowym współczynnikiem zmęczeniowy można przedstawić w postaci iloczynu
, w którym
dotyczy samego materiału (w materiałach budowlanych nie przekracza on na ogół liczby 3 ) , natomiast
jest współczynnikiem karbu , uwzględniającym kształt elementu , rodzaj połączenia i rodzaj obróbki .

CZĘSTOŚĆ DRGAŃ WG WZORU RAYLEYA

energia kinetyczna max sprowadzona do częstości jednostkowej

Przypadki proste

a) jedna masa skupiona

b)kilka mas skupionych

USTROJE O SKOŃCZONEJ LICZBIE STOPNI SWOBODY

do obliczenia wzajemnych relacji przyjęto
jednakowe we wszystkich punktach

Przybliżenie A

Przybliżenie B

DRGANIA WYMUSZONE BEZ TŁUMIENIA USTROJU O SKOŃCZONEJ LICZBIE STOPNI SWOBODY DYNAMICZNEJ

Założenia :

• ustrój o skończonej (n) liczbie st. swobody dynamicznej

• bez tłumienia

• obciążenie
  

• wszystkie obciążenia dynamiczne , to samo
  

• rozważamy drgania ustalone (stan ustalony , nie dotyczą stanu przejściowego)

Obliczenia:

• siły bezwładności (amplitudy)

Założenia :

• n - skończona liczba stopni swobody dynamicznej

• bez tłumienia

• 
  

- częstość kątowa wymuszenia

• ruch ustalony

Wyniki założeń :

-w ruchu ustalonym

- przyspieszenie

Wyznaczenie sił bezwładności (amplitud) generowanych ruchem mas

-amplitudy sił bezwładności

- przemieszczenie w p1 pod wpływem sił bezwładności

Znaki amplitud sił bezwładności należy interpretować odpowiednio do zwrotu sił jakie przyjęto przy wyznaczaniu

Równania do wyznaczenia amplitud sił bezwładności

W tzw. strefie rezonansowej siły bezwładności zdążają do nieskończoności

Tak jest w modelu jaki założyliśmy , w rzeczywistości amplitudy rosną do pewnej wartości (amplitudy największe) nie koniecznie niszczące konstrukcję .

Tłumienie drgań

Tłumienie jest mniejsze im lepiej uporządkowane wnętrze cząstki (np. stal ma bardzo małe tłumienie).

Czynniki wpływające na tłumienie:

• wewnętrzne (wynikające ze struktury próbek)

• konstrukcyjne (w zależności od połączeń, sztywności połączeń itp.)

• środowiskowe, ośrodka (olej, powietrze itp.)

Miary tłumienia:

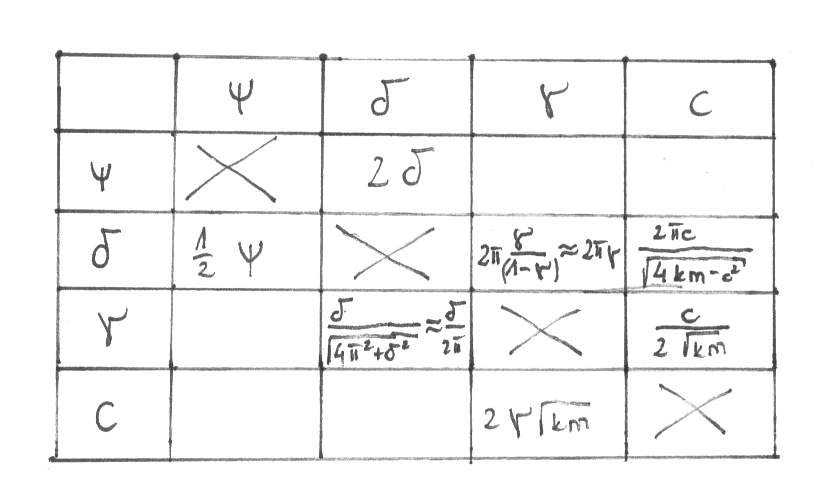
1. Logarytmiczny dekrement tłumienia drgań (otrzymywany doświadczalnie).

-logarytmiczny dekrement tłumienia

2. Współczynnik pochłaniania drgań

3. Współczynnik proporcjonalności siły oporu c.

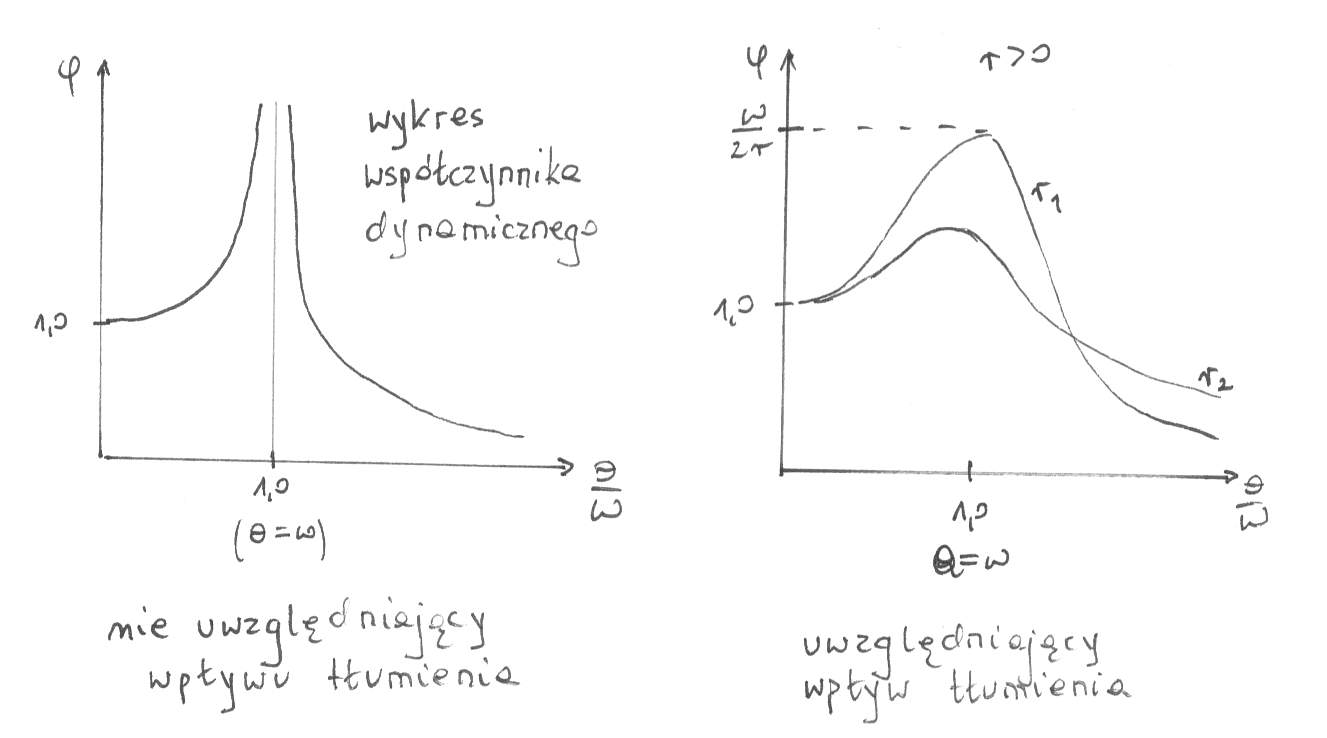
4. Współczynnik dynamiczny

- przemieszczenie wywołane amplitudą siły wymuszającej działającej statycznie

=

-bez tłumienia
-prędkość kołowa maszyny
-podłoża

-z tłumieniem

5. Współczynnik proporcjonalności siły oporu na jednostkę masy

r = c/2m

6. Ułamek tłumienia krytycznego.

Równania ruchu drgań własnych bez tłumienia

Równanie ruchu z tłumieniem

---