PLANIMETRIA

Należy powtórzyć:

• określenie funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym;

• twierdzenie Pitagorasa;

• twierdzenie sinusów;

• twierdzenie cosinusów;

• środek i promień okręgu wpisanego oraz okręgu opisanego

• własności czworokąta opisanego na okręgu i własności czworokąta wpisanego w okrąg;

• pole trójkąta;

• pola czworokątów.

1. W trójkącie prostokątnym ABC, gdzie przy wierzchołku C jest kąt prosty dane są:

Oblicz miary kątów wewnętrznych i długości boków trójkąta.

2. Boki trójkąta mają długość 5 oraz 7. Kąt zawarty pomiędzy nimi ma 60^o. Oblicz długość trzeciego boku i miary pozostałych kątów wewnętrznych.

3. Oblicz obwód trójkąta ABC, w którym mamy dane:
   .

4. Oblicz obwód trójkąta równobocznego wiedząc, że :

1. pole trójkąta jest równe
   

2. wysokość trójkąta ma długość
   ,

3. promień okręgu wpisanego w trójkąt ma dł.
   ,

4. promień okręgu opisanego ma dł.
   .

5. Na trójkącie prostokątnym o przyprostokątnych 8 i 6 opisano okrąg i w ten trójkąt wpisano okrąg. Oblicz jakim procentem pola koła opisanego jest pole koła wpisanego w dany trójkąt.

6. Oblicz stosunek promienia koła wpisanego do promienia koła opisanego na trójkącie o bokach dł. 5, 8, 11.

7. Wykaż, że trójkąt o bokach dł. 5, 7, 11 jest rozwartokątny.

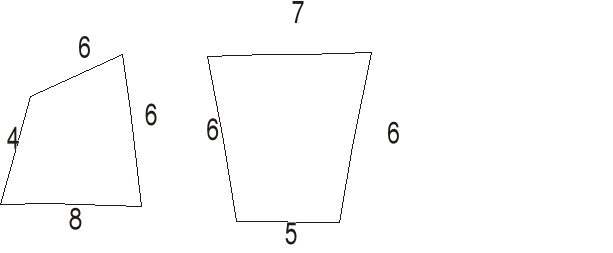
8. Czy na przedstawionym na rysunku czworokącie można opisać okrąg? Odpowiedź uzasadnij.

9. Czy w przedstawiony na rysunku czworokąt można wpisać okrąg? Odpowiedź uzasadnij.

10. Z kawałka materiału w kształcie trapezu prostokątnego o podstawach dł. 3dm i 6dm i krótszym ramieniu dł. 4dm wycięto okrągłą serwetkę. Oblicz jaki % materiału został wykorzystany, a jaki nie.

11. Obwód równoległoboku jest równy 20. Dłuższa przekątna równoległoboku ma dł. 8 i tworzy z krótszym bokiem kąt 60^o. Oblicz miary katów wewnętrznych tego równoległoboku. Oblicz jego pole.

    

2

---