SPRAWOZDANIE
Imię i nazwisko: Marek Dziedzic 05.03.2002
Wydział: Elektronika
Rok: I
Nr ćwiczenia: C
Temat ćwiczenia:
Statystyczna analiza wyników pomiarów
1. Cel ćwiczenia:
Zapoznanie ze statystyczną analizą wyników pomiarów, sposobami znajdowania i eliminacji wyników obarczonych błędami grubymi, oceną składowej przypadkowej błędu, wskazanie na konieczność analizy warunków i wyników pomiarów pod kątem obecności składowej systematycznej błędu.
2. Wykaz przyrządów pomiarowych:
- suwmiarka elektroniczna -rozdzielczość: 0.01 mm
-błąd graniczny: ±0,03 mm
3. Przebieg ćwiczenia:
3.1 Pomiar trójkąta nr 11
a) Pomiar długości boków i wysokości trójkąta :
a, b, c - długości boków: a, b, c
ha, hb, hc - długości wysokości opadających na boki odpowiednio: a, b, c
Pa, Pb, Pc, Ph - pola trójkątów liczone ze wzorów:
Pa=0,5·a·ha Pb=0,5·b·hb Pc=0,5·c·hc
Ph=√p·(p-a)·(p-b)·(p-c) p=0,5·(a+b+c)
Lp. |
a [mm] |
b [mm] |
c [mm] |
ha [mm] |
hb [mm] |
hc [mm] |
1. |
92,81 |
84,98 |
75,26 |
65,08 |
71,13 |
80,31 |
2. |
92,81 |
84,99 |
75,26 |
65,08 |
71,13 |
80,30 |
3. |
92,79 |
84,95 |
75,23 |
65,12 |
71,11 |
80,27 |
4. |
92,76 |
84,95 |
75,24 |
65,10 |
71,12 |
80,24 |
5. |
92,79 |
84,94 |
75,22 |
65,09 |
71,10 |
80,26 |
6. |
93,15 |
84,92 |
75,41 |
65,15 |
71,14 |
80,26 |
7. |
92,79 |
84,94 |
75,24 |
65,28 |
70,96 |
80,29 |
8. |
92,71 |
84,88 |
75,17 |
65,10 |
71,05 |
80,20 |
9. |
92,80 |
84,95 |
75,23 |
65,28 |
71,10 |
80,30 |
10. |
92,77 |
84,94 |
75,25 |
65,13 |
71,13 |
80,30 |
11. |
92,77 |
84,97 |
75,24 |
65,07 |
71,11 |
80,18 |
12. |
92,80 |
84,99 |
75,26 |
65,10 |
71,13 |
80,25 |
xśr |
92,812 |
84,950 |
75,250 |
65,131 |
71,100 |
80,263 |
Sśr |
0,1098 |
0,0310 |
0,0558 |
0,0728 |
0,0504 |
0,0412 |
Tabela nr 1.
Wyznaczenie wartości pola trójkąta:
Lp. |
Pa [mm²] |
Pb [mm²] |
Pc [mm²] |
Ph [mm²] |
1. |
3020,0 |
3022,3 |
3022,1 |
3014,2 |
2. |
3020,0 |
3022,7 |
3021,7 |
3014,4 |
3. |
3021,2 |
3020,4 |
3019,4 |
3012,2 |
4. |
3019,3 |
3020,8 |
3018,6 |
3012,0 |
5. |
3019,9 |
3019,6 |
3018,6 |
3011,6 |
6. |
3034,4 |
3020,6 |
3026,2 |
3023,0 |
7. |
3028,7 |
3013,7 |
3020,5 |
3012,2 |
8. |
3017,7 |
3015,4 |
3014,3 |
3007,2 |
9. |
3029,0 |
3020,0 |
3020,5 |
3012,3 |
10. |
3021,1 |
3020,9 |
3021,3 |
3012,2 |
11. |
3018,3 |
3021,1 |
3016,4 |
3012,6 |
12. |
3020,6 |
3022,7 |
3019,8 |
3014,3 |
xśr |
3022,5 |
3020,0 |
3020,0 |
3013,2 |
Sśr |
5,2 |
2,8 |
3,0 |
3,6 |
Tabela nr 2.
xśr - wartość średnia Sśr - wartość odchylenia standardowego
Analiza i opracowanie wyników pomiarów
Jak wynika z tabeli nr 1 każda seria pomiarów zawiera pomiary obarczone
błędem grubym. I tak pomiar długości:
a - pomiar nr: 6, 8
b - pomiar nr: 8
c - pomiar nr: 6
ha - pomiar nr: 7, 9
hb - pomiar nr: 7
hc - pomiar nr: 8, 11
Po odrzuceniu tych pomiarów liczę parametry rozkładu normalnego (xśr, Sśr) dla skróconej serii:
xśr (m.)- średnia arytmetyczna serii n pomiarów (x1,x2,...,xn ) wielkości fizycznej X wynosi
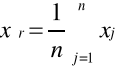
Sśr (s) - Średni błąd kwadratowy pojedynczego pomiaru skończonej serii n pomiarów wielkości fizycznej X wynosi:
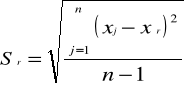
Po określeniu nowych wartości liczę nowe wartości pól z w/w wzorów.
Podczas liczenia pola odrzucone pomiary zastępuję wartością średnią z danej serii. - wyniki pomiarów oznaczone „*”.
Tabela nr 3 zawiera skorygowane serie pomiarowe.
Tabela nr 4 zawiera wartości pól po korekcie.
Lp. |
a [mm] |
b [mm] |
c [mm] |
ha [mm] |
hb [mm] |
hc [mm] |
1 |
92,81 |
84,98 |
75,26 |
65,08 |
71,13 |
80,31 |
2 |
92,81 |
84,99 |
75,26 |
65,08 |
71,13 |
80,30 |
3 |
92,79 |
84,95 |
75,23 |
65,12 |
71,11 |
80,27 |
4 |
92,76 |
84,95 |
75,24 |
65,10 |
71,12 |
80,24 |
5 |
92,79 |
84,94 |
75,22 |
65,09 |
71,10 |
80,26 |
6 |
* |
84,92 |
* |
65,15 |
71,14 |
80,26 |
7 |
92,79 |
84,94 |
75,24 |
* |
* |
80,29 |
8 |
* |
* |
75,17 |
65,10 |
71,05 |
* |
9 |
92,80 |
84,95 |
75,23 |
* |
71,10 |
80,30 |
10 |
92,77 |
84,94 |
75,25 |
65,13 |
71,13 |
80,30 |
11 |
92,77 |
84,97 |
75,24 |
65,07 |
71,11 |
* |
12 |
92,80 |
84,99 |
75,26 |
65,10 |
71,13 |
80,25 |
xśr |
92,789 |
84,957 |
75,237 |
65,102 |
71,114 |
80,278 |
Sśr |
0,0172 |
0,0229 |
0,0258 |
0,0249 |
0,0250 |
0,0249 |
Tabela nr 3
Lp. |
Pa [mm²] |
Pb [mm²] |
Pc [mm²] |
Ph [mm²] |
1. |
3020,0 |
3022,3 |
3022,1 |
3014,2 |
2. |
3020,0 |
3022,7 |
3021,7 |
3014,4 |
3. |
3021,2 |
3020,4 |
3019,4 |
3012,2 |
4. |
3019,3 |
3020,8 |
3018,6 |
3012,0 |
5. |
3019,9 |
3019,6 |
3018,6 |
3011,6 |
6. |
3022,6* |
3020,6 |
3019,3* |
3012,9* |
7. |
3020,4* |
3020,2* |
3020,5 |
3012,2 |
8. |
3020,3* |
3018,1* |
3017,3* |
3010,4* |
9. |
3020,7* |
3020,0 |
3020,5 |
3012,3 |
10. |
3021,1 |
3020,9 |
3021,3 |
3012,2 |
11. |
3018,3 |
3021,1 |
3020,1* |
3012,6 |
12. |
3020,6 |
3022,7 |
3019,8 |
3014,3 |
xśr |
3020,4 |
3020,8 |
3019,9 |
3012,6 |
Sśr |
1,06 |
1,33 |
1,40 |
1,19 |
Tabela nr 4
Obliczenie błędów i określenie przedziałów niepewności wyników
Sx - Średni błąd kwadratowy wartości średniej xśr skończonej serii pomiarów n wielkości fizycznej X wynosi:
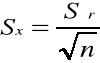
p - błąd przypadkowy graniczny wynosi:
p=k·Sx
dla n=10-11 k=2,26 dla n=12 k=2,2
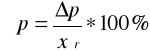
δp - błąd względny przypadkowy wynosi:
x(l) - błąd graniczny suwmiarki
δx(l) - błąd względny suwmiarki wynosi:
δx(l)=l/xśr*100%
Wielkość Mierzona x |
xśr [mm] |
n |
Sśr [mm] |
Sx [mm] |
p=k·Sx [mm] |
x ± p - [mm] + |
δp [%] |
x(l) [mm] |
δx(l) [%] |
|
a |
92,789 |
10 |
0,0172 |
0,0054 |
0,012 |
92,777 |
92,801 |
0,013 |
0,03 |
0,033 |
b |
84,957 |
11 |
0,0229 |
0,0069 |
0,016 |
84,941 |
84,973 |
0,019 |
0,03 |
0,036 |
c |
75,237 |
11 |
0,0246 |
0,0074 |
0,017 |
75,220 |
75,254 |
0,023 |
0,03 |
0,04 |
ha |
65,102 |
10 |
0,0258 |
0,0082 |
0,019 |
65,083 |
65,121 |
0,029 |
0,03 |
0,046 |
hb |
71,114 |
11 |
0,0250 |
0,0075 |
0,017 |
71,097 |
71,131 |
0,024 |
0,03 |
0,042 |
hc |
80,278 |
10 |
0,0249 |
0,0079 |
0,018 |
80,260 |
80,296 |
0,023 |
0,03 |
0,038 |
|
[mm2] |
|
|
|
|
- [mm2] + |
|
|
|
|
Pa |
3020,4 |
12 |
1,06 |
0,31 |
0,7 |
3019,7 |
3021,1 |
0,023 |
- |
- |
Pb |
3020,8 |
12 |
1,33 |
0,38 |
0,9 |
3019,9 |
3021,7 |
0,03 |
- |
- |
Pc |
3019,9 |
12 |
1,40 |
0,40 |
0,9 |
3019,0 |
3021,8 |
0,03 |
- |
- |
Ph |
3012,6 |
12 |
1,19 |
0,34 |
0,8 |
3011,8 |
3013,4 |
0,027 |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
Tabela nr 5
Przykładowe obliczenia:
- bok c:
Sx=0,0246/√12=0,0074 mm
p=2,2·0,0074=0,01628≈ 0,017 mm
x=75,237±0,017 mm
δp=0,017/75,237·100=0,0225≈ 0,023 %
δx(l)=0,03/75,237·100=0,0398≈ 0,04 %
4. Uwagi i wnioski:
Jak wynika z tabeli 3 skrócone serie mają odchylenie standardowe mniejsze od 0.03 więc można przyjąć poprawność obliczeń w dalszej analizie.
Z oczekiwanym prawdopodobieństwem 95% wartości pól obliczonych xe wzoru : p=0.5·|bok|·|wysokość| prawie w całości pokrywają się przedziałami określoności. Oznacza to, że pomiary są prawidłowe, a ponieważ różnice wartości pól są nieznaczne, można stwierdzić że ćwiczenie, zarówno pomiary jak i obliczenia zostały wykonane z dużą dokładnością.
Wartość pola Ph liczona ze wzoru Herona jest zdecydowanie mniejsza od wartości pozostałych pól. Nie jest to spowodowane pomyłką, czy niedokładnością pomiarów. Wynika to ze sposobu liczenia pola.
P=0.5·|bok|·|wysokość| - jest liczeniem w sposób arytmetyczny, natomiast Ph=√p·(p-a)·(p-b)·(p-c) - jest rachunkiem geometrycznym. Ponieważ średnia geometryczna np.: śr=√16·25=20 jest zawsze mniejsza od średniej arytmetycznej sr=0,5·(16+25)=20,5 , dlatego przy dużych liczbach - jak w przypadku pól - te różnice są zauważalne (tabela 5).
![]()
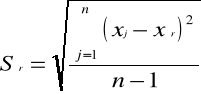
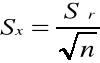
![]()
Wyszukiwarka
Podobne podstrony:
C - Statystyczna analiza wyników pomiarów, Lab C e, Laboratorium miernictwa elektronicznego
Statystyczna analiza wyników pomiarów, Sprawolki
C - Statystyczna analiza wyników pomiarów, Lab C i, Sprawozdanie
Statystyczna analiza wyników pomiarów, Informatyka, Podstawy miernictwa, Laboratorium
C - Statystyczna analiza wyników pomiarów, Lab C g, Laboratorium Miernictwa Elektronicznego
C - Statystyczna analiza wyników pomiarów, spraw.
C - Statystyczna analiza wyników pomiarów, statystyczna analiza wynikow pomiarów(miern), Politechnik
C - Statystyczna analiza wyników pomiarów, mier1
C - Statystyczna analiza wyników pomiarów, Lab C c, Cezary Kozłowski
C - Statystyczna analiza wyników pomiarów, Lab C h, Pomiar
C - Statystyczna analiza wyników pomiarów, SP, Kozieł Piotr
C - Statystyczna analiza wyników pomiarów, KOREK, Marcin Kornak
C - Statystyczna analiza wyników pomiarów, statystyczna anaziza wyn. pomiarˇw
C - Statystyczna analiza wyników pomiarów, spr trˇj, x
C Statystyczna analiza wyników pomiarów lab z mier
C - Statystyczna analiza wyników pomiarów, m-2, Wykona˙ : Grzegorz Kozik
C - Statystyczna analiza wyników pomiarów, cw 1, Protokół z ćwiczenia: Statystyczna analiza wyników
C - Statystyczna analiza wyników pomiarów, Statystyczna analiza wyników pomiarów, Statystyczna anali
C - Statystyczna analiza wyników pomiarów, CW3MIERN, Zespół Szkół Elektronicznych
więcej podobnych podstron