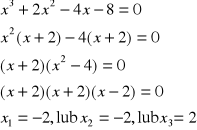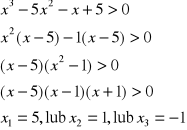III. WIELOMIANY
W(x) = a0 + a1x + a2x2 + … +anxn ,gdzie a1, a2, …, an np. W(x) = 3 + 5x - x2 + 7x3 - 3x4. |
|
|
|
|
|
|
|
|
|
|
22
5
-1
+
+
1
|
|
|
![]()
![]()
Wyszukiwarka
Podobne podstrony:
dzialania na wielomianach
Nierownosci wielomianowe
dzielenie wielomianów
WIELOMIANY, Zadania przygotowujące do matury z matematyki
4 4 Wielomiany
Kiełbasa wielomiany
4 Rozkład wielomianów na ułamki proste
wielomiany, Do Matury, Matematyka
Obliczanie wartosci wielomianów schemat Hornera
nierówności wielomianowe
Praca nauczyciela to nieustanne poruszanie się po terenie naszpikowanym wieloma psychologicznymi
wielomiany rzeczywiste spelniające podane warunki
Mathcad Wielomiany Lagrange (1)
działania na wielomianach
IS Matematyka C S 05 wielomiany f wymierna
lista2 wielomiany
więcej podobnych podstron