PRACA DOMOWA NR 4 Z MATEMATYKI (Logistyka, studia dzienne, I rok)

Zad. 1. Korzystając z definicji granicy ciągu, pokazać, że:

a)
, b)
, c)
.

Zad. 2. Wyznaczyć granice ciągów:

a)
, b)
, c)
, d)
, e)   
, f)
, g)
, h)
,
i)   
, j)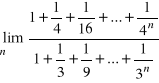
, k)
, l)
,
ł)   
, m)
, n)
, o)
,
p)   
, r)
, s)
, t)
,
u)
, w)
.

Wskazówki do wybranych przykładów z zad. 2:

do k): należy podzielić wszystkie wyrażenia przez najwyższą potęgę w mianowniku (tj., tu przez
),

do l): należy zauważyć, że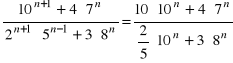
, a następnie podzielić wszystkie wyrażenia przez najwyższą potęgę w mianowniku (tj., tu przez
),

do u): ponieważ
i
, to
i dalej należy skorzystać z twierdzenia o 3-ech ciągach,

do w): należy zauważyć, że dla każdego
,
, a zatem:

,
,
, . . . ,
.

Odpowiedzi do zad. 2:

a)
, b)
, c)
, d)
, e)
, f)
, g)
, h)
, i)
, j)
, k)
, l)
, ł)
,
m)
, n)
, o)
, p)
, r)
, s)
, t)
, u)
, w)
.

---