PRACA DOMOWA NR 8 Z MATEMATYKI (Logistyka, studia dzienne, I rok)

Zad. 1. Korzystając z definicji pochodnej funkcji w punkcie, wyznaczyć wzór na pochodną funkcji
w punkcie
, jeśli: a)
,
, b)
,
.

Zad. 2. Korzystając z definicji pochodnej funkcji w punkcie, wyznaczyć ogólne wzory na pochodne funkcji z zad. 1.

Zad. 3. Wyznaczyć pochodne podanych funkcji, korzystając z odpowiednich wzorów:

a)
, b)
, c)
, d)
,
e)
, f)
.

Zad. 4. Wyznaczyć pochodne następujących funkcji złożonych:

a)
b)
, c)
, d)
, e)
, f)
, g)
, h)
, i)
, j)
,
k)
, l)
, ł)
, m)
.

Odpowiedzi do zadań:

Zad. 1: a)
, b)
;

Zad. 2: a)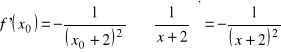
, b)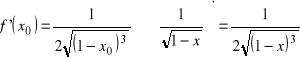
;

Zad. 3: a)
, b)
, c)
,
d)
, e)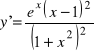
, f)
;

Zad. 4: a)
, b)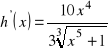
, c)
,
d)
, e)
, f)
, g)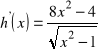
, h)
, i)
, j)
, k)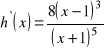
, l)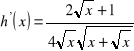
,
ł)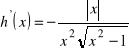
, m)
.

---