LOGIKA I METODOLOGIA NAUK #5

• Żeby myśleć używamy pojęć, które z kolei mają zakresy (zbiory). Jeśli wywód jest precyzyjny, to da się go zapisać symbolicznie (ale na odwrót nie zawsze).

ZBIORY

PROSTE ZŁOŻONE

PEŁNY PUSTY ILOCZYN SUMA RÓŻNICA DOPEŁNIENIE

Zbiór pełny (U)

x = y

identyczność

• Definicja identyczności Leibneza

x = y
∀_F (F_x
F_y)

Dwa przedmioty są identyczne wtedy i tylko wtedy, gdy wszystkie ich cechy są takie same.

U = {x: x jest niesprzeczny} = {x: x = x}

Każdy przedmiot jest identyczny ze sobą samym.

Zbiór pełny - uniwersum ontologii

• Uniwersum danej nauki - to zbiór wszystkich przedmiotów rozważanych przez tę naukę.

uniwersum geometrii = zbiór pełny geometrii

• 
  Najszerszym uniwersum jest zbiór pełny ontologii.

Ø = {x: x ≠ x}

• 
  
  
  Zbiór pusty - zbiór obiektów, których nie ma.

• ILOCZYN ZBIORÓW

X
Y = {x: x
X
x
Y}

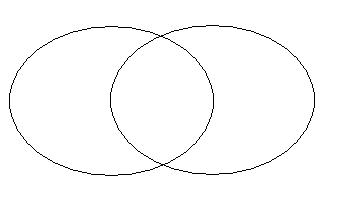
Przykłady:

• X = róże (zbiór róż)

Y = rzeczy czerwone (zbiór rzeczy czerwonych)

X
Y = róże czerwone (zbiór róż czerwonych)

• X = przyczyny zdarzeń
  Y = ludzie
  X
  Y = sprawcy zdarzeń (czyli ludzie, o ile są przyczynami zdarzeń)
  

• 
  
  X = róże
  Y = liczby parzyste
  X
  Y = Ø
  
  

• 
  X = ludzie
  Y = kobiety
  X
  Y = zbiór kobiet

- iloczyn jest przemienny

• X = uniwersum
  Y = róże
  X
  Y = róże

∀_x ( X
U = x) ∀_x ( X
X = X) ∀_x ( X
Ø = Ø)

• X = kobiety
  Y = Ø
  X
  Y = Ř
  

• X = zbiór wszystkich drzew
  Y = zbiór wszystkich lasów
  X
  Y = Ř

• X = rowery
  Y = kierownice
  X
  Y = Ř
  

• X = ludzie
  Y = akty psychiczne
  X
  Y = Ř

• SUMA ZBIORÓW
  

X
Y = {x: x
X
x
Y}

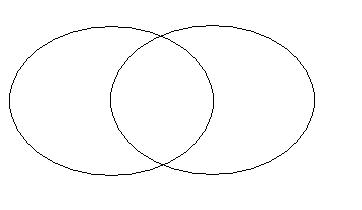
• X = podniety działania (poznawcze)
  Y = pobudki działania (uczuciowe)
  X
  Y = motywy działania (czyli podniety lub pobudki)
  

• X = przedstawienia odtwórcze
  Y = przedstawienia wytwórcze
  X
  Y = wyobrażenia
  

• X = mężczyźni
  Y = kobiety
  X
  Y = ludzie dorośli
  

• X = uniwersum
  Y = ludzie
  X
  Y = uniwersum
  

• X = kobiety
  Y = Ř
  X
  Y = kobiety
  

∀_x ( X
U = U) ∀_x ( X
X = X) ∀_x ( X
Ø = Ø)

• RÓŻNICA ZBIORÓW

X - Y = {x: x
X
x
Y}

(/)

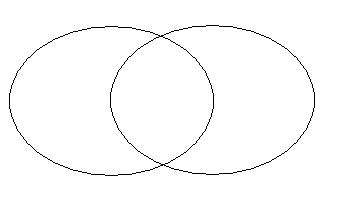
Różnica nie jest symetryczna, nie jest wszystko jedno co się od czego odejmie.

• X = spotkania drużyn piłkarskich
  Y = rozstrzygnięte gry sportowe
  X - Y = nierozstrzygnięte gry sportowe
  

• X = ludzie młodzi
  Y = pracujący zarobkowo
  X - Y = młodzi bezrobotni
  

• X = kobiety
  Y = mężczyźni
  X - Y = kobiety
  

• X = istoty żywe
  Y = organizmy
  X - Y = bezkomórkowe
  

• X = działania
  Y = czyny zgodne z prawem
  X - Y = czyny bezprawne

X
Y = Ø X - Y = X

X
Y = Ø Y - X = Y

• DOPEŁNIENIE ZBIORU (różnica U - zbioru)

- X = U - X

(X')

• X = przedmioty
  Y = uniwersum
  -X = przedmioty niematerialne
  

• U = ludzie
  X = wierzący
  - X = ateiści
  

• U = sprawcy
  X = poczytalni
  - X = niepoczytalni
  

• U = przedmioty
  X = byty
  - X = przedmioty nie będące bytami
  

A = {a, b, c} B = {c, d} C = {c, a} U = Z (zwierzęta)

1. B
   ((A-B)
   A) = B
   ({a,b}
   {a, b, c}) = {c, d}
   {a, b} = {a, b, c, d}
   

2. ((( C - B)
   (A - C))
   - B)
   A = (({a}
   {b})
   -{c, d})
   {a, b, c} = (Ø
   -
   {c, d})
   {a, b, c} = Ø
   { a, b, c} = Ø
   

3. ((-A
   B)
   ({c}
   C)) - (U
   B) = ((-{a, b, c}
   {c, d})
   ({c}
   {c, a})) -
   (U
   {c, d}) = ({d}
   {c, a}) - {c, d} = {a, c, d} - {c, d} = {a}
   
   
   

• STOSUNKI MIĘDZY ZBIORAMI

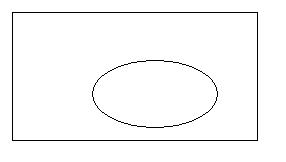
1. Stosunek zamienności lub pokrywania się zakresów pojęć

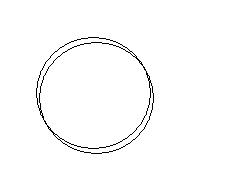
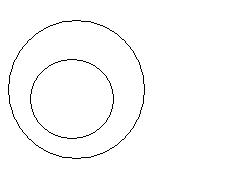
1)'Stosunek inkluzji ( zawierania się)

X

S = psycholog dziecięcy S= człowiek
P = psycholog P= ssak rozumny

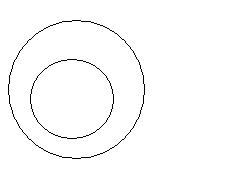
2. Stosunek podrzędności (inkluzji właściwej)

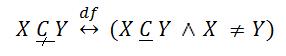
Np. S = psycholog dziecięcy S = czyn nakazany

P = psycholog P = czyn dozwolony

3. Stosunek krzyżowania się zakresów pojęć

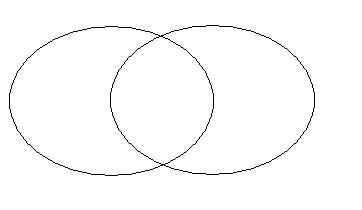
Np. S = Polak S = nauczyciel S = norma moralna
P = psycholog P = kobieta P = norma prawna

Luka tutaj to znak krzyżowania

4. Stosunek rozłączności, wykluczania się

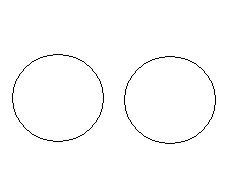
Stosunek rozłączności to stosunek przeciwieństwa lub stosunek sprzeczności:

• stosunek przeciwieństwa

Ta luka między X a Y to znak rozłączności

Np. U = zwierzęta S = pies P = kot

U = czyny S = czyn nakazany P = czyn zakazany

U = czyny S = czyn dobry P = czyn zły

• 
  
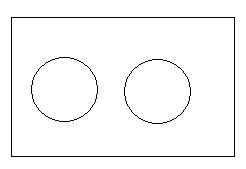
  stosunek sprzeczności zakresowej

Np. U = ludzie S = teiści P = ateiści
U = czyny S = czyny moralne P = czyny niemoralne

U = zdania S = prawdziwe P = fałszywe lub obojętne

uniwersum
psychologii

uniwersum
arytmetyki

uniwersum
geometrii

X

Y

X
Y

K

L

X

Y

X -Y

Y

X
Y

U

- X

X

X

Y

X

Y

X = Y
∀_x (x
X
x
Y)

X

Y

X

Y

X

zawiera się

zawiera się

Y

Y

X

---