MIKROEKONOMIA - WYKŁAD DLA STUDIÓW DOKTORANCKICH W ZAKRESIE PRAWA

Program:

1. Na czym polega ekonomiczne myślenie (znaczenie teorii ekonomicznej, racjonalność i korzyść własna)

2. Mechanizm rynkowy. Popyt i podaż (analiza popytu i podaży, równowaga rynkowa, autoregulacja równowagi)

3. Polityka mikroekonomiczna rządu (ceny gwarantowane, podatki, dotacje, limity, cła, dumping)

4. Teoria konkurencji: koszty produkcji, konkurencja doskonała, monopol, konkurencja niedoskonała

5. Teoria gier i teoria ryzyka

Literatura:

1. E. Mansfield, Podstawy mikroekonomii, Zasady, przykłady, zadania,

Agencja Wydawnicza, Warszawa 2000

2. T. Kamińska, B. Kubska-Maciejewicz, J. Laudańska-Trynka, Teoria podejmowania decyzji przez podmioty rynkowe, Wyd. UG, wydania od 2000 r

3. Z. Dach, Mikroekonomia dla studiów licencjackich, Synaba, Kraków 2005

4. B. Czarny, Podstawy ekonomii, PWE, Warszawa 2004

5. R.F. Frank, Mikroekonomia jakiej jeszcze nie było, GWP, Gdańsk 2007

EKONOMICZNE MYŚLENIE

Ekonomia jest nauką o dokonywaniu wyborów dotyczących gospodarczej sfery życia na tle sprzeczności między potrzebami i możliwościami ich realizacji.. Wyboru dokonuje konsument, przedsiębiorstwo, rząd, inwestor, pracodawca, pracobiorca, organizacja, także pozarządowa.

Potrzeby ludzkie są nieograniczone i zawsze większe od możliwości ich zaspokojenia. Wynika to bezpośrednio z faktu ograniczoności zasobów czynników wytwórczych, której konsekwencją jest zjawisko rzadkości.

Podmioty gospodarujące dokonują ciągłego wyboru wariantów wykorzystania czynników wytwórczych będących w ich dyspozycji. Wybór ten łączy się z ponoszeniem kosztu alternatywnego, którym jest utrata najlepszej, niewybranej możliwości zastosowania posiadanych zasobów oraz czas, dlatego można go też określić jako koszt utraconych możliwości lub korzyści.

Zależności między rzadkością, wyborem i kosztem alternatywnym pokazuje graficznie krzywa możliwości produkcyjnych, zwana też krzywą transformacji. Nachylenie tej krzywej to krańcowa stopa transformacji MRT określająca, o ile należy zmniejszyć produkcję jednego dobra, aby zwiększyć produkcję drugiego dobra o jednostkę (coś za coś - ang. trade off).

Możliwości produkcyjne poszczególnych podmiotów nie są określone raz na zawsze. Ich wzrost lub spadek powoduje odpowiednie przesunięcie KMP.

Krzywa możliwości produkcyjnych KMP

spódnice

Zatrudnienie		Produkcja
spodnie	spódnice	spodnie	spódnice
0 1 2 3 4 5	5 4 3 2 1 0	0 5 9 12 14 15	15 14 12 9 5 0

0 5 10 15 spodnie

Gospodarka jest to mechanizm prowadzący do alokacji czynników wytwórczych między konkurencyjne zastosowania oraz do dystrybucji dochodu. Dzięki temu mechanizmowi można odpowiedzieć na fundamentalne pytania ekonomii:

1. co i ile produkować?,

2. jak produkować?,

3. dla kogo produkować?

Wszystkie wyprodukowane dobra stanowią produkt narodowy, a w ujęciu pieniężnym dochód narodowy.

Od końca XIX wieku ekonomia zajmuje się również innymi ograniczeniami - oprócz rzadkości zasobów - wpływającymi na wybory podmiotów rynkowych. Należą do nich instytucje, rozumiane jako wzorce i normy postępowania wyznaczone przez zwyczaje, moralność i prawo. Instytucje te ograniczają wybory ekonomiczne ze względu na przyzwyczajenia człowieka lub przez swoją represyjność.

Metoda ekonomii

TEORIA

Obieg okrężny dóbr i pieniądza

MECHANIZM RYNKOWY

Rynek to proces uzgadniania wszelkich warunków dostaw i zakupu (rodzaj, ilość i cenę dóbr i usług, formę zapłaty, warunki transportu i gwarancji). Istotą mechanizmu rynkowego są nie zakłócane ingerencją organów administracji państwowej procesy dostosowawcze popytu i podaży, w rezultacie których dochodzi do wykształcenia się ceny i wielkości równowagi w określonym czasie i przestrzeni geograficznej. Dla istnienia rynku niezbędne jest występowanie co najmniej dwóch podmiotów wymiany, tj. producenta - sprzedawcy i konsumenta - nabywcy. Współcześnie nawiązywanie stosunków wymiennych może odbywać się za pomocą telefonu, faxu lub internetu.

Popyt to wielkości zgłaszanego zapotrzebowania na dane dobro przy każdym z poziomów cen tego dobra, którą nabywcy są skłonni i są w stanie zakupić w danym czasie, przy założeniu, że inne czynniki wpływające na popyt pozostają bez zmian (ceteris paribus). Jego ilustracją graficzną ilustracją jest - na ogół - opadająca krzywa popytu.

baryłka 150

ropy w $ 125

100

50

30

25

20

15

10

5

0

1973 1990 1995 2000 .05 .06 01.08 05.08 08.08 09.08 lata

Wielkość popytu (rozmiary popytu), ilustrowana punktem na krzywej popytu, oznacza wielkość zapotrzebowania przy danym poziomie ceny. Opadający przebieg krzywej popytu jest ilustracją prawa popytu, mówiącego, iż wielkość popytu zmienia się w przeciwnym kierunku do zmiany ceny, tj. gdy cena spada, wielkość popytu rośnie i vice versa. Jeśli zmienia się cena danego dobra, z analizy graficznej zmian w sferze popytu dokonuje się przesuwając się po krzywej popytu; zmiana któregoś z tzw. czynników pozacenowych, powoduje przejście na nową krzywą popytu.

W rezultacie popyt na dane dobro jest funkcją ceny dobra, dochodu kupujących, poziomem cen dóbr substytucyjnych i komplementarnych, liczbą nabywców (ich strukturą wieku, płci, wykształcenia, zawodów), preferencji nabywców (upodobania, gusty wynikające z tradycji, zwyczaje, naśladownictwo, moda), oczekiwania co zmiany cen i dochodów, sytuacja gospodarcza i polityczna kraju.

cena baryłki 150

ropy 125

100

50

30

25

20

15 D_05.08

10

5 D_09.08 D₂₀₀₀

0

1 2 3 4 5 6 7 8 9 10 baryłki

cena

baryłki S_09.08 S₂₀₀₀ S₂₀₀₅

5,0

4,5

4,0

3,5

3,0

2,5

2,0

1,5

1,0

0,5

0,0

1 2 3 4 5 6 7 8 9 10 baryłki

Podaż to zestawienie różnych wielkości ofert towarowych przy różnych poziomach ceny rynkowej, czyli relacja pomiędzy ilością dóbr dostarczonych na rynek a ich cenami w określonym czasie. Jest ona ilustrowana krzywą podaży. Wielkość podaży to punkt na krzywej podaży oznaczający wielkość oferty określonego dobra przy danym poziomie ceny. Krzywa podaży jest rosnąca, ponieważ - zgodnie z prawem podaży - wraz ze wzrostem ceny, ceteris paribus, wielkość podaży rośnie. Zmiany ceny oferowanego towaru powodują - w analizie graficznej - przesuwanie się po krzywej podaży, zmiana w obrębie czynników pozacenowych - wywołuje przejście na nową krzywą podaży.

cena

baryłki S₂₀₀₀

150

125

100

50

30 A

25

20

15

10 B

5 D₂₀₀₀

0

1 2 3 4 5 6 7 8 9 10 baryłki

Podobnie jak w wypadku popytu, podaż jest funkcją ceny dobra oraz technologii i kosztów produkcji, przewidywań producentów odnośnie do zmiany cen i popytu w przyszłości, liczby przedsiębiorstw w branży, interwencjonizmu państwowego, warunków naturalnych i czynników losowych, sezonowości produkcji, rozmiarów importu i eksportu, czasu.

Zrównanie wielkości popytu i podaży, a więc przecięcie się krzywej popytu z krzywą podaży wyznacza cenę i wielkość równowagi rynkowej.

Różnica między ceną, jaką gotowi są zapłacić konsumenci za określoną ilość dobra a ceną, jaką faktycznie płacą nazywa się rynkową nadwyżką konsumentów (w odróżnieniu od nadwyżki konsumenta). Różnica między ceną, jaką otrzymują producenci za sprzedaż określonej ilości produktu a ceną, po której byliby skłonni już ją sprzedać nazywa się rynkową nadwyżką producentów (w odróżnieniu od nadwyżki producenta).

NARZĘDZIA INTERWENCJI RZĄDU NA RYNKU

Ze względu na bezduszność mechanizmu rynkowego programy wspierające redystrybucję dochodu i korygujące ceny - szczególnie w rolnictwie - są powszechnie stosowane w świecie. Do najpowszechniej wykorzystywanych narzędzi interwencji w mechanizm rynkowy należą:

1. cena maksymalna i minimalna

2. system podatkowy

3. subsydia (dotacje)

4. kwoty produkcyjne

5. taryfy i kwoty importowe

6. dumping

Programy wspierające producentów lub konsumentów wykorzystywane są głównie w odniesieniu do rolnictwa i przybierają różnorodną formę. W zamian za ograniczenie przez rolników powierzchni zasiewów zbóż lub roślin pastewnych rząd zobowiązuje się skupić płody rolne po gwarantowanych cenach minimalnych, gdyby cena równowagi była niższa od gwarantowanej. W rolnictwie mają zastosowanie także kwoty produkcyjne i kwoty importowe w celu podtrzymania krajowych cen rynkowych. W rezultacie interwencja rządu nie dopuszcza do ukształtowania się efektywnej alokacji rzadkich zasobów, czyli uniemożliwia strukturę produkcji zgodnie z najwyższym kosztem utraconych możliwości (kosztem alternatywnym).

Ponadto interwencja powoduje poprawę sytuacji majątkowych jednych grup społecznych kosztem zubożenia innych. Rolnicy korzystający z wsparcia cenowego często organizują się w grupy interesu, walczące o utrzymanie takich programów rządowych, podczas gdy grupy konsumentów i podatników są jej przeciwne. Do analizy skutków wymienionych narzędzi interwencji będzie zastosowane podejście od strony równowagi cząstkowej, skupiającej się na rynku pojedynczego dobra, gdy żaden z uczestników rynku (producenci i nabywcy) nie dysponuje siłą rynkową, tj. nie może wpływać na wysokość ceny rynkowej, lecz posiada pełną o nich informację.

Aby zbadać, jak zakłócenie na jednym rynku wpływa na rynki dóbr substytucyjnych i komplementarnych oraz czynników wytwórczych należałoby zastosować podejście od strony równowagi ogólnej (globalnej). Wówczas można określić warunki równowagi na wszystkich rynkach jednocześnie. Jednak wnioski, jakie wynikają z równowagi cząstkowej (efekty pierwotne ingerencji rządowej) mogą nie zbiegać się z wnioskami z równowagi ogólnej.

Dlaczego równowaga jest efektywna ekonomicznie?

P_X

20 V

18

16

14 S

12

10 U S_X

8 A E

6 T Z

4 W

2

0

1 2 3 4 5 6 7 8 9 10Q_X

Nadwyżka konsumentów to pole Δ AVE. Nadwyżka producentów to pole Δ AWE.

Dobrobyt społeczny to suma nadwyżek producentów i konsumentów, czyli pole Δ WVE.

Odpowiedzi na to pytanie można dokonać porównując zarówno dobrobyt społeczny w punkcie równowagi i innych punktach z krzywych popytu i podaży, jak i za pomocą kosztów produkcji i korzyści, osiąganych przez nabywców.

Ustalenie ceny minimalnej i maksymalnej

P_X

S

P_MIN nadmiar

P_E

P_MAX niedobór

D

0 Q_K Q_P Q_E Q_K Q_P Q_X

Cena maksymalna chroni nabywcę, a cena minimalna stanowi wsparcie dla producenta. W efekcie zarówno krzywa popytu, jak i podaży jest złamana.

Obciążenie podatkiem pośrednim (akcyza)

P_X

20 V

18 S + T

16

14 N

12 L

10 T S_X

8 A K E

6 M

4 W

2

0

1 2 3 4 5 6 7 8 9 10Q_X

Obciążenie podatkiem T odcinek MN

Wpływy do budżetu MN x AM = pole ð ALNM

Obciążenie nabywców = pole ð ALNK =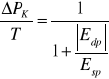

Obciążenie producentów = pole ð WAKM =

Nieefektywność rynku (strata dobrobytu) pole Δ MNE

Rezultaty obciążenia podatkiem dobra na rynku o rosnącej krzywej podaży i malejącej krzywej popytu sprowadzają się do:

1. mniejszej produkcji w porównaniu do efektywnego poziomu

2. nadwyżki konsumentów i producentów spadną w porównaniu do efektywnego poziomu

3. wpływ na budżet jest pozytywny, ponieważ następuje wpływ środków do budżetu, które następnie zostaną rozprowadzone w innych sektorach gospodarki

4. przychody z podatku są mniejsze niż spadek nadwyżek konsumentów i producentów, zatem podatek powoduje spadek korzyści ekonomicznych netto (zmniejszenie dobrobytu społecznego).

Dotacje kwotowe

P_X

20

18 S

16 A

14

12 B C

10 J S - T

8 E G K

6 F

4

2

0

1 2 3 4 5 6 7 8 9 10Q_X

Nadwyżka konsumentów pole A + B + E + G + K

Nadwyżka producentów pole F + E + B + C

Wydatki budżetu E + B + C + J + K + G

Nieefektywność rynku = pole Δ J

Ekonomiczny sens dotacji (subsydiów) sprowadza się do ujemnego podatku, czyli kwotowej dopłaty rządu do każdej wyprodukowanej jednostki dobra. Rezultaty wprowadzenia dotacji są przeciwne do rezultatów wprowadzenia podatku, czyli:

1. produkcja rynkowa przewyższa poziom efektywny

2. nadwyżki konsumentów i producentów są wyższe niż bez dotacji

3. wpływ dotacji na budżet jest negatywny, ponieważ rząd środki na ten cel musi zgromadzić z innych dziedzin gospodarki

4. wydatki rządowe na dotacje są większe niż wzrost nadwyżek producentów i konsumentów, co prowadzi bezpośrednio do straty dobrobytu społecznego.

Kiedy rząd chce podtrzymać cenę na poziomie powyżej ceny równowagi może również ograniczyć wielkość produkcji. Może to zrobić wprowadzając kwoty produkcyjne dla każdego producenta lub limit ich sprzedaży. Kwoty spełniają funkcję podobną do cen maksymalnych na rynku, tyle że od strony podaży. Szczególnie znane jest ich zastosowanie na rynku artykułów rolnych (np. produkcja mleka, areał zasiewów różnych roślin), ale też znana jest kontrola usług przewozowych (liczba taksówek w mieście), kontrola wykonywania wolnych zawodów (korporacje zawodowe). Te programy mają na celu wspieranie producentów w danym sektorze.

kwoty produkcyjne

cena

mleka

limit

S

C

A

B

0 Q_P mleko

Programy rządowe podtrzymujące cenę - choć w rezultacie kosztowne dla podatników - są wykorzystywane wszędzie tam, gdzie niskie ceny rynkowe zagrażają dochodom rolników. Do narzędzi interwencji rynkowej zalicza się również limitowanie areału upraw poszczególnych roślin i skup płodów rolnych.

Ograniczenie zasiewów ma być bodźcem do utrzymywania produkcji poniżej poziomu wolnorynkowego poprzez dopłatę do hektara nieobsianej powierzchni ziemi uprawnej. Istota tego narzędzia sprowadza się do następującego mechanizmu: jeżeli rząd chce utrzymać cenę np. buraków cukrowych na poziomie P_min, to liczy się z możliwością wchłonięcia przez rynek produkcji na Q_K; rolnicy po tej cenie zaoferują rynkowi Q_P, lecz są skłonni do rezygnacji z nadmiernej produkcji Q_KQ_P pod warunkiem uzyskania dopłaty do każdego odłogowanego hektara. Korzyści netto z takiego działania rządu wynoszą suma nadwyżek konsumentów i producentów pomniejszona o wypłatę z budżetu. Zatem program prowadzi do zwiększenia nadwyżki producenta o sumę pól ABC, co kosztuje rząd sumę pól BCG. Strata dobrobytu społecznego wynosi sumę pół BG.

kompensata za rezygnację z produkcji roślinnej

cena

buraków

cukrowych

S

P_min

A B C

G

D

0 Q_K Q_P buraki

Skup nadmiernej produkcji

cena

pszenicy

S

F

P_min

A B C

G J

E D + zakupy rządowe

H

D

s k u p

0 Q_K Q_P pszenica

Jako alternatywny program rządowy może być wykorzystany skup produkcji rolnej przez agencje rządowe (np. skup zbóż). Wówczas rząd, chcąc utrzymać cenę tony pszenicy na poziomie wyższym od ceny wolnorynkowej, skupuje nadmierną podaż. Nadwyżka producentów pozostaje niezmieniona w porównaniu do poprzedniego rozwiązania, jednak koszt takiego przedsięwzięcia jest znacznie wyższy, gdyż obejmuje sumę pól HGBCJ. Ten koszt mógłby by obniżony poprzez sprzedaż skupionych płodów na rynku światowym nawet po niższej cenie. W przeciwnym razie zmagazynowana produkcja rolna musiałaby być sprzedana po pewnym czasie, co nieuchronnie spowodowałoby obniżkę pierwotnej ceny i w rezultacie doprowadziłoby do skutków przeciwnych do zamierzonych.

Korzyści społeczne netto wynoszą: nadwyżka konsumentów F + nadwyżka producentów EABCG - koszt skupu HGBCJ. Strata dobrobytu społecznego wynosi pole BGHJ.

Instrumentami polityki ochrony rynku wewnętrznego (protekcjonizmu) przed konkurencją zagraniczną są cła i kwoty importowe. Oba instrumenty pozwalają utrzymać wyższą produkcję krajową sprzedawaną na rynku wewnętrznym po wyższej cenie. Faworyzują producentów kosztem konsumentów i ostatecznie prowadzą do straty dobrobytu społecznego.

W warunkach gospodarki otwartej bez stosowania polityki ochrony rynku krajowego konsumpcja dobra wzrośnie i konsumenci znacznie podwyższą swoją nadwyżkę (suma pól ABC). Spadnie produkcja krajowa i zmniejszy się nadwyżka producentów (zamiast G + A uzyskają jedynie G).

Nałożenie cła podniesie rentowność produkcji krajowej, co spowoduje jej wzrost a spadnie zapotrzebowanie i niezbędny import. To stanowi wyjaśnienie, dlaczego producenci krajowi bardzo często tworzą silne lobby za stosowaniem ceł lub ich podnoszeniem. Pobrane cła tworzą przychód do budżetu (pole H) i stanowią korzyści netto dla gospodarki, gdyż mogą być wykorzystane w innym zastosowaniu. W efekcie strata dobrobytu wynosi sumę pól BC.

Ten sam skutek rząd może osiągnąć wprowadzając ograniczenie importu poprzez wyznaczenie maksymalnej kwoty importowej. Istnieje jednak istotna różnica między tymi instrumentami; wprowadzając kwoty importowe rząd rezygnuje z przychodów uzyskanych z ceł, które stają się częścią nadwyżki producentów zagranicznych, gdyż sprzedają po cenie wyższej od światowej.

Dopłata rządu (dotacja) do produkcji krajowej w celu zwiększenia udziału kraju w rynku światowym często określona jest mianem dumpingu. Producenci w kraju - importera ponoszą straty nadwyżki, konsumenci korzystają na obniżonych cenach, czyli wzrost ich nadwyżki jest finansowany przez rząd kraju eksportera.

C Ł A

20

S_K S_K

F F

8

A B C E cena światowa + cło

6 cena światowa A B H C

4

G G

2

I M P O R T IMPORT

0 Q_K Q_E Q_D 0 Q_K Q_T Q_D

rynek pszenicy

wolny rynek rynek chroniony cłem

kwoty importowe

20

S_K

S_K + kwota

8

6

cena światowa

4

2

D

I M P O R T

0 Q_K Q_D pszenica

dumping

cena

lekarstwa S_K

F

P_W E

A I B H C J

P_W - T

G

D

0 Q_K1 Q_K Q_D1 Q_D lekarstwo

Nadwyżka konsumentów w kraju importera to suma pól FEAIBHC

Nadwyżka producentów G

Udział budżetu kraju eksportera równa się sumie pól IBHCJ

KOSZTY PRODUKCJI

Ekonomiczne myślenie opiera się - jak wiadomo - na koszcie alternatywnym, co w tym wypadku sprowadza się do wyboru wynikającego z kosztów ekonomicznych (TC). Są one sumą kosztów jawnych i ukrytych. Koszty jawne to wydatki, jakie firma musi ponieść na zakup czynników wytwórczych oraz amortyzacja, która jest kosztem jawnym, ale nie jest wydatkiem. Koszty ukryte to koszty, jakie firma musiałaby ponieść zakupując czynniki wytwórcze będące w jej posiadaniu, np. koszty dzierżawy hali produkcyjnej, gdyby nie była jej właścicielem. Inaczej mówiąc, koszty ekonomiczne obejmują pełny rachunek kosztów związanych z określoną działalnością gospodarczą i różnią się od kosztów księgowych, które uwzględniają jedynie koszty jawne. W związku z tym odróżnia się zysk ekonomiczny od zysku księgowego.

Zysk ekonomiczny zysk normalny strata ekonomiczna

gdy TR>TC=C_e+C_i gdy TR=TC gdy TR<TC

lub P>ATC lub P=ATC lub P<ATC

to ∏_e>0 to ∏ _e=0 to L_e>0

Proces produkcyjny charakteryzuje się możliwością natychmiastowych przystosowań firmy do zmian zachodzących w jej otoczeniu (czynniki zmienne) i jednocześnie sztywnością reakcji w odniesieniu do majątku trwałego. Konsekwencją jest konieczność uwzględnienia czasu w podejmowaniu decyzji i podział kosztów w krótkim okresie na stałe (TFC) i zmienne (TVC). W długim okresie występują jedynie koszty zmienne, bowiem firma może zmienić także swoją wielkość, tj. może rozszerzać lub kurczyć swoje możliwości produkcyjne.

Zatem w krótkim okresie:

TC=TFC+TVC,

jeśli obie strony podzielimy przez wielkość produkcji x, to:

, gdzie: ATC- przeciętny koszt całkowity, AFC - przeciętny koszt stały i AVC- przeciętny koszt zmienny.

ATC = AFC + AVC

W podejmowaniu decyzji istotną rolę odgrywa koszt krańcowy (MC), definiowany jako zmiana kosztów całkowitych spowodowana zmianą produkcji o jednostkę. Ponieważ w krótkim okresie zmieniają się jedynie koszty zmienne, zatem koszty krańcowe zmieniają się tylko pod wpływem kosztów zmiennych. Toteż

.

MODELE RYNKU

Model rynku	Liczba producentów	Rodzaj produktu	Podejmowane decyzji	Wejście na rynek	Mobilność czynników produkcji	Wynik ekonomiczny w długim okresie
Konkurencja doskonała	bardzo dużo	jednorodny	- wielkość produkcji	pełna wolność	pełna	zysk normalny
Konkurencja monopolistyczna	wielu	zróżnicowany	- wielkość produkcji - cena	pełna w długim okresie	niepełna	zysk normalny
Oligopol	od dwóch do kilkunastu	jednorodny lub zróżnicowany	- wielkość produkcji - cena	ograniczona lub brak	niepełna	zysk ekonomiczny
Monopol	jeden	jednorodny	- wielkość produkcji - cena	brak	niepełna	zysk ekonomiczny

Przedsiębiorstwo na rynku konkurencji doskonałej

Bez względu na rodzaj konkurencji, w jakiej uczestniczy firma, jej celem gospodarowania jest maksymalizacja zysku (minimalizacja straty) w krótkim okresie i maksymalizacja wartości firmy w okresie długim. Cel krótkookresowy jest osiągany dla wielkości produkcji, przy której koszt krańcowy jest równy przychodowi krańcowemu, czyli MC=MR. Na rynku konkurencji doskonałej firma jest biorcą ceny i dlatego podejmuje tylko jedną decyzję o wielkości produkcji (sprzedaży).

Prowadząc działalność produkcyjną w krótkim okresie, w zależności od poziomu kosztów i ceny rynkowej dobra, firma może w punkcie równowagi:

• osiągać zysk ekonomiczny, gdy TR>TC lub P>ATC,

• osiągać zysk normalny, gdy TR=TC lub P=ATC,

• minimalizować stratę, gdy TVC<TR<TC lub AVC<P<ATC lub L_e<TFC; TVC=TR lub AVC=P lub L_e=TFC oznacza punkt zamknięcia firmy,

• zawiesić produkcję, gdy TVC>TR lub AVC>P lub L_e>TFC.

Poza optimum ekonomicznym firma osiąga dolny próg rentowności przechodząc z obszaru strat do zysków dla niskich poziomów produkcji i górny próg rentowności przy wysokim poziomie produkcji, wychodząc z obszaru zysku, gdy TR=TC lub P=ATC.

MONOPOL

Podobnie jak inni producenci w gospodarce rynkowej, monopol próbuje maksymalizować zysk, podejmując - w odróżnieniu od firmy na rynku doskonale konkurencyjnym - dwie decyzje:

1. o wielkości produkcji (sprzedaży),

2. o poziomie ceny.

Jak każda firma maksymalizująca zysk (minimalizująca stratę) osiąga optymalne parametry (wielkość produkcji i cenę), gdy przychód krańcowy MR zrównuje się kosztem krańcowym MC.

Ponieważ dla monopolu, który jest jedynym producentem na rynku dobra nie posiadającego najczęściej bliskiego substytutu (np. elektrownia, gazownia czy przedsiębiorstwo zaopatrujące w wodę), krzywa popytu rynkowego D jest jednocześnie krzywą popytu na produkt firmy d. Jeśli firma chce sprzedać większą ilość produktu, musi obniżyć cenę nie tylko na tę dodatkową ilość sprzedaży, lecz na wszystkie jednostki skierowane na rynek w danym czasie.

Cena jest wyższa od przychodu krańcowego (P>MR), a krzywa przychodu krańcowego MR leży poniżej krzywej popytu rynkowego dla każdego poziomu cen. W rezultacie krzywa przychodu całkowitego jest odwróconą parabolą. Monopol jest zainteresowany sprzedażą tylko na odcinku elastycznego popytu, ponieważ przychód całkowity rośnie wraz ze spadkiem sprzedaży, gdy elastyczność cenowa popytu jest większa od (-1).

Monopol, ze względu na siłę monopolową równą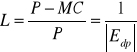
, może różnicować ceny w trojaki sposób:

1. doskonale (I-ego stopnia) - gdy oferuje każdą jednostkę dobra po cenie równej korzyści (użyteczności) krańcowej nabywcy,

2. (II-go stopnia) - gdy nie zna krzywej popytu na swój wyrób i ustala różne ceny za takie same ilości dobra różnym nabywcom,

3. niedoskonale (III-go stopnia) - gdy dokonuje segmentacji rynku ze względu na różną wrażliwość (elastyczność) cenową popytu poszczególnych grup nabywców.

Konkurencja niedoskonała

Niedoskonała konkurencja obejmuje dwie struktury rynkowe:

1. konkurencję monopolistyczną - w branży występuje wiele niezależnych firm, wytwarzających zróżnicowane produkty zaspokajające te same potrzeby (restauracje, stacje benzynowe, firmy odzieżowe, firmy kosmetyczne) i w związku z tym wykorzystujące szeroko reklamę, posiadających pewną siłę rynkową do stanowienia cen. Wejście na rynek monopolistyczny nie wymaga pokonania barier. W rezultacie krzywa popytu na produkt firmy jest funkcją malejącą;

2. oligopol - na rynku znajduje się kilka firm, które stanowią ceny na swoje produkty biorąc pod uwagę decyzje konkurentów, produkt może być zarówno jednorodny, jak i zróżnicowany, istnieją bariery wejścia; firmy w oligopolu mogą tworzyć porozumienia w celu zdominowania rynku (kartel) lub występować niezależnie. W pierwszym przypadku ich decyzje przypominają zachowanie monopolu, w drugim - popyt na swoje wyroby odbierają jako złamaną krzywą popytu.

osiągać zysk ekonomiczny, gdy TR>TC lub P>ATC zysk normalny, gdy TR=TC lub P=ATC

zł zł

MC

MC ATC

P_E

ATC P_E

MR D=d=AR MR D=d=AR

0 q_E produkcja (sprzedaż) 0 q_E

TC TC

TR TR

Kartel

firma 1 firma 2 rynek

Podział kwot produkcyjnych następuje według formuły:

MR = Σ MC = MC₁ = MC₂

Przywódca cenowy

Rynek pewnego dobra jest rynkiem oligopolistycznym i znajduje się w równowadze, gdy pojawia się na nim lider cenowy.

Zł S

MC

D

MR

oligopol ze złamaną krzywą popytu

jp

MC

P_e

dn

d_f

E_dp>(-1)

0 Xe MR Qx

TR

jp

0 Xe Qx

TEORIA GIER

Teoria gier - definiowana jako teoria podejmowania decyzji w warunkach interaktywnych (gry strategicznej) lub inaczej matematyczna teoria sytuacji konfliktowych - została stworzona przez J. von Neumanna, który stwierdził, że istota tej gry nie polega na próbie odgadnięcia intencji gracza, lecz na skrywaniu własnych zamiarów. Podstawowym założeniem teorii gier jest racjonalne działanie wszystkich podmiotów decyzyjnych (graczy). Podstawowymi elementami każdej sytuacji, w której występuje zjawisko konkurencji są:

1. Gracze i ich posunięcia. Na rynku występuje przynajmniej dwóch graczy i ich działania inwestycyjne, marketingowe oraz produkcyjno - cenowe są wzajemnie uzależnione.

2. Wyniki i wypłaty. Działania wszystkich graczy określają wynik walki konkurencyjnej (zwany wartością gry). Każdemu możliwemu wynikowi odpowiada określona wypłata, która jest miarą stopnia osiągnięcia celu każdego z rywali; najczęściej wyrażona pieniężnie, gdy mowa o przedsiębiorstwie, a w wartościach użyteczności, gdy dotyczy konsumenta.

3. Reguły gry i cele graczy. Postępowaniem graczy rządzą formalne i nieformalne reguły gry. Mogą to być przepisy prawne, powszechnie uznane zasady konkurencji i nieuczciwe praktyki lub wrogie przejęcia, a także zasób wiedzy analitycznej umożliwiającej śledzenie zachowań konkurencyjnych.

Punktem wyjścia w każdej analizie konkurencji, odwołującej się do dorobku teorii gier, jest opis graczy, stosowanych przez nich strategii, rozumianych jako plan działań, uwzględniający wszystkie ewentualności, w jakich gracz może się znaleźć, oraz uzyskanych przez każdego z nich wypłat.

Walka konkurencyjna może mieć charakter jednorazowego posunięcia lub wielu działań rozłożonych w czasie (konkurencja sekwencyjna i powtarzalna).

Gry mogą występować w wersji strategicznej i ekstensywnej.

.Gry niekooperacyjne, jednorazowe i jednoczesne

Czysty konflikt i strategie minimaksu i maksiminu

Najlepszym wynikiem, jakiego może oczekiwać gracz uczestniczący w grze o sumie zerowej (sytuacja czystego konfliktu obu stron) przeciwko jednakowo nastawionemu rywalowi, jest osiągnięcie stanu równowagi, który występuje, gdy oczekiwania obu podmiotów zostają potwierdzone w rzeczywistości. Gdyby któryś z graczy odstąpił od realizacji strategii prowadzącej do równowagi, ograniczyłby wielkość własnych wypłat i pozwoliłby na zwiększenie wypłat rywala.

W i e r s z	Kolumna
			A	B	C	D
		A	12	-1	1	0
		B	5	1	7	-20
		C	3	2	4	3
		D	-16	0	0	16

Celem Wiersza jest taki wybór wiersza z największą wartością, natomiast Kolumny była liczba jak najmniejsza.

W i e r s z	Kolumna
			A	B	C	D
		A	12	-1	1	0
		B	5	1	7	-20
		C	3	2	4	3
		D	-16	0	0	16

Para strategii C Wiersza i B Kolumny daje wynik będący punktem równowagi, gdyż Wiersz zapewnia sobie wygraną co najmniej 2, Kolumna grając B gwarantuje, że Wiersz wygra najwyżej 2. Wypłata dla danej pary strategii jest najmniejsza w wierszu i najwyższa w kolumnie. Oboje wybierając te strategie mają gwarancję, iż nie uzyskają wyniku gorszego niż wybrany.

Strzałki na diagramie prowadzą do rozwiązania, gdy w poszczególnych wierszach prowadzi się strzałkę z każdej komórki do komórki z najmniejszą wartością, natomiast w kolumnach - z każdej komórki do komórki z największą wartością w danej kolumnie.

Wynik gry macierzowej (dla macierzy zawierającej wypłaty gracza wybierającego wiersze, nazywa się punktem siodłowym, jeżeli jego wartość jest mniejsza lub równa każdej wartości w jego wierszu, a większa lub równa każdej wartości w jego kolumnie.

Dla każdej gry macierzowej, dla której istnieje taka liczba v, że Wiersz ma strategię gwarantującą mu wygranie co najmniej v, a Kolumna ma strategię gwarantującą, że Wiersz nie wygra więcej, v jest wartością gry.

Jeśli gra ma punkt siodłowy, to jego wartość jest wartością gry. Gra może mieć kilka punktów siodłowych, zawierające je strategie są najbezpieczniejsze.

W i e r s z	Kolumna				minimum wiersza
		A B C D	A	B	C	D
				4	3	2	5		2
				-10	2	0	-1		-10
				7	5	2	3		2
				0	8	-4	-5		-5
maksimum kolumny		7	8	2	5

minimaks maksimin

Jeżeli maksimin (największa z najmniejszych wartości) wierszy i minimaks (najmniejsza z największych wartości) kolumn jest taki sam, oznacza to, że leży on w punkcie siodłowym. Powyższa gra ma dwa punkty siodłowe. Gdy maksimin nie jest równy minimaksowi, to gra nie ma punktu siodłowego.

Dwa przedsiębiorstwa A i B, w macierzy udział w rynku A, to udziały B wynoszą 1 minus udział A.

	B1	B2	B3
A1 A2 A3	0,8 0,45 0,6	0,35 0,28 0,5	0,3 0,7 0,9

Przedsiębiorstwo A, kierując się maksymalizacją udziału w rynku wybierze strategię maksiminu, a B minimaksu.

Strategia dominująca to najlepsza możliwa reakcja na dowolną strategię zastosowaną przez konkurenta. Jej logika nieuchronnie prowadzi do pogorszenia wyniku, gdy gra ma charakter niekooperacyjny

Historycznym przykładem gry niekooperacyjnej jest dylemat więźnia.

Gra dwuosobowa aresztowanych

D z i a ł a n i a A	D z i a ł a n i a B Nie przyznawać się wsypać kompana
Nie przyznawać się	1 rok 1 rok	10 lat 0 lat
Wsypać kompana	0 lat 10 lat	5 lat 5 lat

Paradoks więźnia występuje w ekonomii, gdy partnerzy skazani są na nieoptymalny wynik. Ze względu na brak bodźców, żaden nie zamierza jednostronnie zmienić swojego zachowania, chyba że w drodze podjęcia skoordynowanej współpracy, opartej na zaufaniu. Ten rodzaj strategii można wykorzystać do wyjaśnienia oszustwa w porozumieniach kartelowych.

Jeśliby dwa przedsiębiorstwa stworzyły kartel, dający zyski na poziomie 6 mln PLN i dzielone po połowie, to uwzględniono by to w polu a (3, 3). Rywale zdają sobie sprawę, że jeśli zwiększą sprzedaż, a konkurent pozostanie wierny umowie, to ich zyski wzrosną do 3,5 mln PLN, lecz uczciwym spadną do 1,5 mln PLN. Jeśli obaj będą oszukiwać, to zrealizują zyski na poziomie 2 mln PLN.

F I R 1 M A	F I R M A 2
			oszustwo	uczciwość
		oszustwo	2 2	3,5 1,5
		uczciwość	1,5 3,5	3 3

Zysk kartelu jest maksymalny, gdy oba przedsiębiorstwa postępują zgodnie z umową kartelową, a najniższy, gdy oba oszukują partnera. W tym najgorszym, pod względem wyniku, polu (d) ukształtowała się równowaga, ponieważ partnerzy dostrzegają możliwość zwiększenia swojego zysku przez nielojalność wobec siebie.

Strategie zapewniające równowagę (gry o wejście na rynek, udział w rynku) powinny być stosowane, gdy konkurenci podejmują decyzje niezależnie od siebie (brak zmowy). Wówczas są odzwierciedleniem „optymalnej” reakcji obu graczy, czyli pozwalają one zmaksymalizować wielkość wypłaty każdego z nich w warunkach, określonych przez wybór strategii, dokonany przez przeciwnika (równowaga Nasha). Inaczej, równowaga Nasha oznacza taką parę strategii, że żaden z graczy nie ma motywacji do jednostronnego odejścia od przyjętej strategii, biorąc pod uwagę strategię zastosowaną przez drugiego (dylemat więźnia powyżej).

Najlepszym wynikiem, jakiego może oczekiwać gracz uczestniczący w grze o sumie zerowej przeciwko jednakowo nastawionemu rywalowi, jest osiągnięcie stanu równowagi. Gdyby któryś z graczy odstąpił od realizacji strategii prowadzącej do równowagi, ograniczyłby wielkość własnych wypłat i pozwoliłby na zwiększenie wypłat rywala.

Ponieważ równowaga Nasha może się ukształtować w położeniu nieoptymalnym dla podmiotów rynkowych, ekonomiści zwracają uwagę na strukturę rynku i konkurencję między podmiotami, w której najkorzystniejsze rozwiązanie łączy się z wyczerpaniem potencjału rynku w poszukiwaniu okazji do poprawy alokacji.

Prostym przykładem gry, ilustrującej koncepcję równowagi Nasha, w której przynajmniej dwaj gracze dokonują jednego, jednoczesnego ruchu, dotyczącego podjęcia jednej decyzji, jest konkurencja między Hondą i Toyotą w Ameryce Północnej pod koniec lat 90. związana z budową nowych zakładów produkcyjnych

Gra o udział w rynku między Toyotą i Hondą

T o y o t a

Budować nową wytwórnię Nie budować

Budować nową wytwórnię

H o n d a

Nie budować

Wartości gry są podane w mln dolarów.

Z opisanego przykładu wynika, że jeśli gracze oczekują racjonalnego zachowania się przeciwnika, to obaj „optymalizując” wybór, osiągają równowagę Nasha.

Na polskim rynku paliwowym Orlen jest przedsiębiorstwem znacznie większym od Rafinerii Gdańskiej. Oba przedsiębiorstwa myślą o ekspansji, która prowadzi do różnych wyników, mierzonych poziomem zysku w mln zł w zależności od zachowania rywala.

O r l e n	Rafineria Gdańska
		Inwestować	inwestować	nie inwestować
				12 4	20 3
		nie inwestować	15 6	18 5

1. którą strategię wybiorą rywale?

2. czy na rynku istnieje równowaga Nasha?

Przykładem gier z więcej niż jedną równowagą Nasha jest gra w tchórza, w której dwóch nastolatków najeżdża na siebie samochodami po jednopasmowej drodze. Pierwszy, który zjedzie z drogi zostaje tchórzem, drugi - bohaterem. Jeżeli obaj zjadą z drogi, to obaj zostają tchórzami. Jeżeli żaden nie zjedzie - obaj lądują w szpitalu.

I R E K	J A N E K
		Zjechać	zjechać	nie zjechać
				1 1	1 2
		nie zjechać	2 1	0 0

Nie występują strategie dominujące, lecz dwie równowagi Nasha. Ekonomistów zawsze intrygowało poszukiwanie w życiu gospodarczym przykładów zachowań, które odpowiadałyby postawom brawurowych graczy. Wydaje się, że najbardziej zbliżona jest sytuacja monopolu naturalnego, w którym wysokie koszty wejścia i malejące koszty przeciętne nie pozwalają realizować rentowności umożliwiającej funkcjonowanie na rynku dwóch przedsiębiorstw.

Telewizja kablowa jest branżą wymagającą wysokich nakładów kapitału (kosztów stałych) i relatywnie niskich kosztów krańcowych wraz z podłączeniem następnego subskrybenta do odbioru programów. Zatem próg rentowności wymaga znacznej liczby odbiorców (gospodarstw domowych). Ponieważ rynek telewizji satelitarnej w Wielkiej Brytanii na przełomie lat 90. XX. wieku wydawał się potencjalnie ogromny, więc dwie firmy postanowiły go podbić. Specyfikę sytuacji kształtowała odmienna, niekompatybilna technologia obu konkurentów zniechęcająca odbiorców do opłacenia 200 funtów opłaty wstępnej z ryzykiem braku możliwości wykorzystania sprzętu, gdyby zaszła konieczność przestawienia się na odbiór proponowany przez inną firmę. Ponadto, firma Sky Television planowała wziąć w leasing już krążącego w przestrzeni satelitę, a British Satellite Broadcasting (BSB) zamierzała umieścić w przestrzeni własnego satelitę, co znacznie podnosiło jej koszty.

W tabeli zamieszczono szacunek wartości zaktualizowanej wartości netto NPV za lata 1989 - 1999 uwzględniającej koszty satelitów, oprogramowania, reklamy, sprzedaży i kosztów administracyjnych w warunkach dwóch strategii każdej z firm (wejścia na rynek i pozostania poza nim).

S K Y	B S B
			wejść	nie wchodzić
		Wejść	- 118 - 747	673 0
		nie wchodzić	0 137	0 0

Układ efektów (wypłat) wskazuje, że występuje podwójna równowaga Nasha. Teoria gier nie podpowiada, która równowaga jest lepsza. To zależy od uwzględnienia dodatkowych informacji (szczegółów). W opisywanym przypadku nie ma miejsca na rynku dla dwóch przedsiębiorstw. Ze względu na opóźnienie techniczne w wystrzeleniu satelity i wysoki poziom dziennych strat z tego tytułu doprowadziły do przejęcia BSB przez Sky. W rezultacie od 1993 roku brytyjski rynek telewizji kablowej jest znacząco rentownym monopolem.

Występowanie kilku stanów równowagi (równowaga wielokrotna) to przypadek nawet najprostszych negocjacji, których rezultatem może być dowolny podział zysków wskutek przyjęcia konkretnego stanu równowagi.

Z ilustracji graficznej wojny cenowej między Elektro Word (z hasłem „u nas najtaniej”) i Media Markt („najniższe ceny nie dla idiotów”) wynika, że gra na obniżkę ceny może prowadzić do bankructwa obu przedsiębiorstw, gdyż prześciganie się w obniżkach ceny prowadzi do ceny równej zeru.

ceny

Elektro World

0 ceny Media Markt

Jednakże w praktyce możliwości obniżki ceny są ograniczone ze względu na koszty (ceny zakupu od producenta), VAT i marżę. Pamiętając, że zyski przedsiębiorstwa nie zależą tylko od własnej strategii, lecz również od strategii konkurenta, a ustalanie ceny poniżej kosztu własnego jest niezgodne z prawem i nie może trwać w dłuższym czasie, każde przedsiębiorstwo musi zadecydować, kiedy pobierać normalne ceny i powstrzymać się od kontrreakcji.

(MC < P_B < P_m). Jeśli przy cenie wynoszącej np. 15 jp. popyt rynkowy wynosiłby Q_X = 60, to każde z dwóch przedsiębiorstw sprzedając po 30 jednostek, realizowałoby zysk na poziomie 150 jp. Gdyby jeden z konkurentów uznał, że może powiększyć zysk poprzez zwiększenie udziału w rynku dzięki obniżce ceny do 14 jp., licząc na lojalność drugiego, to jego sprzedaż wzrosłaby do 40 jednostek, a zysk do 160 jp. Wówczas lojalny partner sprzedałby 25 jednostek, uzyskując jedynie 125 jp. zysku. Przy jednoczesnym wyłamaniu się z umowy, oba przedsiębiorstwa sprzedają po 35 jednostek, z których zyski wynosi po 140 jp. dla każdego.

F I R 1 M A	F I R M A 2
		cena	15	14
		15	150 150	125 160
		14	160 125	140 140

Porozumienie odnośnie do ceny nie stanowiło równowagi Nasha, gdyż obie firmy miały bodźce do wyłamania się z pierwotnych ustaleń. Z powyższego wynika również, że wojna cenowa może trwać do zrównania się ceny z kosztem krańcowym, ponieważ doprowadzi to do zaniku stymulatora obniżki ceny.

W wielu rzeczywistych sytuacjach rywale odpowiadają kontrposunięciami na swoje działania. W grze sekwencyjnej uczestnicy wykonują swe ruchy po kolei (drzewo gier).

Odstraszanie od wejścia

utrzymać cenę 4, 6

wejść

obniżyć cenę - 4, 4

nie wchodzić 0, 12

wejść

6, 4

utrzymać cenę

nie wchodzić

12, 0

wejść 4,- 4

obniżyć cenę

nie wchodzić 9, 0

A. Blinder przedstawił grę, której stronami są władze monetarne FED (niewybieralne, kadencja 14 lat, a prezesów do emerytury) i politycy, którzy muszą starać się o reelekcję. Pierwsi skłonni do polityki restrykcyjnej - drudzy do ekspansywnej. Celem gry jest skłonienie przeciwnika do podjęcia decyzji, której nie chce podjąć z własnej woli. FED preferuje nadwyżkę przychodów budżetu nad wydatkami rządowymi (brak deficytu).

Rezerwa Federalna

Restrykcyjność Bierność Ekspansywność

3 9	1 6	4 4
2 8	5 5	6 1
7 7	8 3	9 2

Teoria ryzyka

Ryzyko oznacza możliwość osiągnięcia wartości końcowej kapitału (inwestycji, instrumentu finansowego) różniącej się od wartości oczekiwanej.

Działanie w warunkach ryzyka, dotyczy podejmowania decyzji odnośnie do zdarzeń, które mogą wystąpić z określonym prawdopodobieństwem.

Zatem o tym, że ktoś działa w warunkach ryzyka, można mówić wtedy, kiedy jego decyzja dotyczy zdarzeń, które mogą wystąpić z określonym prawdopodobieństwem. Jest ono liczbą z przedziału [0,1], która pokazuje, ile razy dane zdarzenie wystąpi, jeśli określona sytuacja powtórzy się wielokrotnie:
, gdzie: p - prawdopodobieństwo wystąpienia badanego zdarzenia, m - liczba powtórzeń zdarzenia, M - liczba prób.

• Niepewność jest czymś innym niż ryzyko; jest pojęciem szerszym, gdyż nieznane jest prawdopodobieństwo wystąpienia zdarzenia. Problem niepewności występuje w rzeczywistości ekonomicznej, kiedy podejmujący decyzję nie znają konsekwencji swojego wyboru.

Niepewność interpretuje się niekiedy przez wprowadzenie czynnika czasu, dla którego przyszłość nie jest znana, więc o wystąpieniu zdarzeń lub zjawisk można twierdzić z określonym prawdopodobieństwem. Dla całego szeregu przewidywanych skutków zdarzeń nie zawsze jest możliwe określenie prawdopodobieństwa wystąpienia każdego z nich. Gdzie można określić którekolwiek z trzech rodzajów prawdopodobieństwa: matematyczne, statystyczne lub szacunkowe, tam występuje ryzyko. Inaczej mówiąc, ryzyko definiuje się w kontekście znajomości rozkładu prawdopodobieństwa. Miary prawdopodobieństwa są jednocześnie miarami ryzyka. Prawdopodobieństwo zdarzenia zawiera się 0≤ p ≤1; jeśli prawdopodobieństwo zdarzenia W wynosi p, to ryzyko jego niewystąpienia wynosi (1-p). Jeśli niemożliwe jest określenie prawdopodobieństwa jakiegoś zdarzenia, to działalność odbywa się w warunkach niepewności. Niejednokrotnie w procesie podejmowania decyzji można oszacować wielkości zdarzeń (stopa zwrotu z inwestycji w różnych wariantach projektu), ale niemożliwe jest przypisanie im prawdopodobieństwa. Ryzyko można określić jako mierzalną niepewność. W literaturze spotyka się zamienne stosowanie obu pojęć.

Zachowania w przypadku ryzyka i niepewności

Grami nazywa się sytuacje, kiedy wyniki o pewnej wartości pieniężnej pojawiają się z różnym prawdopodobieństwem.

Z punktu widzenia gracza, któremu zależy na wygranej, jedną z najważniejszych cech gry jest jej wartość oczekiwana (EV), czyli suma jej wyników pomnożonych przez prawdopodobieństwo ich pojawienia się. Informuje ona o przeciętnym wyniku wielu partii tej gry.

EV (w₁, w₂, p₁, p₂) = p₁∙w₁ + p₂∙w₂,

gdzie: w₁ i w₂ - wypłaty; p₁, p₂ - prawdopodobieństwo, z którym wystąpi wypłata.

Rodzaje gier

Jeśli istnieje 50%-owa szansa zarobienia 1000 PLN, to znaczy, że istnieje jednocześnie 50%-we prawdopodobieństwo utraty tej kwoty pieniędzy (rzut monetą). Udział w takiej grze nie przynosi - przeciętnie rzecz biorąc - szansy na zarobienie pieniędzy. Stąd też taką grę nazywa się uczciwą. Czyli gra uczciwa to taka gra, w przypadku której zyski - przeciętnie rzecz biorąc - są równe zeru.

Jeśli szansa wygrania w/w sumy pieniędzy wynosiłaby 30%, a szansa przegrania 70%, to taką grę nazywa się nieuczciwą. Grając w nią - przeciętnie rzecz biorąc traci się pieniądze.

Gdyby sytuacja była odwrotna, tj. 70%-we prawdopodobieństwo wygranej i 30%-we przegranej, to gra byłaby korzystna, ponieważ udział w grze przeciętnie przyniósłby zysk.

Nie zawsze ludzie biorą udział w grach dobrowolnie. Przypuśćmy, że ktoś posiada domek letniskowy warty 20 tys. PLN na skraju Borów Tucholskich. Niech prawdopodobieństwo włamania do niego i straty 10 tys. PLN wynosi 10%, a prawdopodobieństwo tego, że do włamania nie dojdzie i właściciel ani nie straci, ani nie zyska wynosi 90%. Życie zmusza do udziału w takiej grze.

EV₁ = -1000 * 0,5 + 1000 * 0,5 = 0 zł.

EV₂ = -1000 * 0,7 + 1000 * 0,3 = - 400 zł.

EV₃ = 1000 * 0,7 + (- 1000) * 0,3 = 400 zł.

EV₄ = -10 000 * 0,1 + 0 * 0,9 = - 1000 zł.

Biorąc pod uwagę kryterium wyniku wartości oczekiwanej gry dzielą się na korzystne, uczciwe (sprawiedliwe) i niekorzystne (nieuczciwe).

Kryterium

wynik wartości oczekiwanej skala zmienności wyników

i

częstotliwość pojawiania się ich wartości skrajnych

uczciwe

(sprawiedliwe)

korzystne (EV=0) mniej ryzykowne (WG₁)

(EV>0) WG₁ < WG₂ bardziej ryzykowne (WG₂)

niekorzystne WG₁ < WG₂

(nieuczciwe)

(EV < 0)

Gra jest bardziej ryzykowna, im większy jest rozrzut jej wyników i im częściej pojawiają się wyniki najbardziej oddalone od wartości oczekiwanej gry.

Grając o 100 zł za pomocą rzutu monetą, może wypaść orzeł lub reszka z jednakowym prawdopodobieństwem 0,5. Wówczas EV₁ = 0,5 * 100 + 0,5 * (-100) = 0

Podobnie, rzucając kostką, możemy wyrzucić parzystą lub nieparzystą liczbę oczek. Jeśli parzysta oznacza wygraną 1000 zł, a nieparzysta stratę 500 zł, to

EV₂ = 0,5 * 1000 + 0,5 * (-500) = 250 zł.

Dla gry w rzucanie monetą wyniki 100 zł i -100 zł pojawiają się z takim samym prawdopodobieństwem jak dla gry w kości, ale wyniki są 1000 zł i - 500 zł. Druga gra jest bardziej ryzykowna niż gra pierwsza. Z tymi grami nie można porównać gry z domkiem letniskowym, ponieważ za duża jest różnica zarówno wyników, jak i prawdopodobieństw. Istnieje zatem potrzeba bardziej precyzyjnej miary ryzyka związanego z udziałem w grze.

Za dokładną miarę zmienności wyników gry (ryzykowność gry) uznaje się wariancję gry (WG). Jest ona sumą podniesionych do kwadratu odchyleń wyników gry od jej wartości oczekiwanej, zważonych prawdopodobieństwem wystąpienia tych wyników, czyli

, gdzie:

w_s -wynik gry, p_s - prawdopodobieństwo ich wystąpienia.

W przypadku gry w rzucanie monetą o 100 zł, której wartość oczekiwana EV = 0, wariancja gry wynosi:

WG₁ = 0,5 (100 zł)² + 0,5 (-100 zł)² = 0,5*10 000 zł + 0,5*10 000 zł =

= 5000 zł + 5000 zł = 10 000 zł

W grze w kości, której wartość oczekiwana EV = 250, wariancja tej gry równa się

WG₂ = 0,5 (1000 zł - 250 zł)² + 0,5 (-500 zł - 250 zł)² =

= 281 250 zł + 281 250 zł = 562 500 zł.

Dla gry w letnisko, której wartość oczekiwana wynosi - 1000 zł, wariancja gry równa się: WG₃ = 0,9 (0+1000 zł)² + 0,1(-10 000 zł + 1000 zł)² = 900 000 zł +8 100 000 zł =

= 9 000 000 zł.

Im niższa wariancja, tym niższe ryzyko.

Wynika stąd, że gra w kości jest bardziej ryzykowna od gry w rzucanie monetą, lecz mniej ryzykowna od gry w domek letniskowy.

Załóżmy, że ktoś posiada dom o wartości 500 000 PLN i że prawdopodobieństwo utracenia go wskutek pożaru lub powodzi wynosi 10%. Tym samym szanse utrzymania dotychczasowego stanu posiadania (500 000 PLN) są równe 90%, zaś szanse stracenia wszystkiego wynoszą 10%. Życie zmusza do przyjęcia tego zakładu. Przeciętnie właściciel uzyska 450 000 PLN, czyli 90% od sumy 500 tys. zł plus 10% od zera. Firma ubezpieczeniowa oferuje ubezpieczenie pełnej wartości domu za 100 000 PLN. Sumę tę należy wpłacić niezależnie od tego, czy dom spali się, czy też pozostanie nienaruszony. Natomiast jest ona zobowiązana do wypłacenia odszkodowania w wysokości 500 000 zł tylko wtedy, gdy dom spłonie lub zostanie zalany. A zatem, bez względu na to, czy dom spłonie, czy nie, wartość majątku wyniesie 400 000 zł.

Postawy ludzi wobec ryzyka

Typ człowieka	Decyzja o udziale w grze	Ubezpieczenie przy niekorzystnych stawkach
Unikający ryzyka (asekurant)	Aby zagrać potrzebuje przewagi szans na wygraną	Wykupi polisę
Neutralny wobec ryzyka	Nie zagra, gdy widoki na wygraną są niekorzystne	Nie wykupi polisy
Skłonny do ryzyka (ryzykant, hazardzista)	Zagra nawet wtedy, gdy prawdopodobieństwo przegranej przeważa	Nie wykupi polisy

Czy dom zostanie ubezpieczony? Towarzystwo ubezpieczeniowe wykorzystuje tę sytuację i w ten sposób zarabia pieniądze. Jeśli właściciel nie skorzysta z jego oferty, jego średni wynik wyniesie 450 tys. zł. Jednak wynik rzeczywisty może być równy 500 tys. lub zeru. Ubezpieczenie gwarantuje pewny wynik w wysokości 400 tys. zł. Osoba neutralna odrzuci ofertę, ponieważ zgodnie z kalkulacją matematyczną bardziej opłaca się podjęcie ryzyka, że dom spłonie lub zostanie zalany. Oferta zostanie również odrzucona przez osobę skłonną do ryzyka (hazardzistę), ponieważ ubezpieczenie nie daje szans na wygraną, a zabiera przyjemność odczuwania ryzyka. Osoba z awersją do ryzyka (asekurant) zdecyduje się na ubezpieczenie, bo suma tracona w stosunku do przeciętnego wyniku (50 tys. zł) nie wydaje się zbyt wygórowaną ceną za uniknięcie możliwej katastrofy.

Użyteczność z osiągania korzyści:

• osoby neutralnej wobec ryzyka przyjmuje postać funkcji użyteczności U(w) = a⋅w

• asekuranta -
  

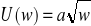
• ryzykanta - U(w) = aw².

(a) (b)

U(w)

U(w)=aw^1/2 U(w) = aw²

U(w₂₎ B

U(EV) p₁

EU E

p₂ U(w₂₎ B

U(w₁) p₁

A

EU E

U(EV)
p₂

U(w₁) A

0 w₁ CE EV w₂ wypłaty 0 w₁ EV CE w₂

Możliwość pojawienia się obu poziomów korzyści z niejednakowym, lecz określonym prawdopodobieństwem p₁ i p₂ pozwala obliczyć wartość oczekiwaną (EV) wyrażoną równaniem: EV = p₁w₁ + p₂ w₂, którego graficzna postać kryje się za odcinkiem AB. Przy rozkładzie prawdopodobieństwa p₁/p₂ wartość oczekiwana znajduje się tam, gdzie w₁EV/EVw₂=p₂/p₁ (E). Prawidłowością jest wyższa użyteczność w warunkach pewności (krzywa U(w) niż użyteczność oczekiwana EU dla każdego poziomu korzyści o prawdopodobieństwie zdarzenia mniejszym od jedności (krzywa AB) dla podmiotu niechętnego ryzyku (a).

Odwrotna prawidłowość występuje w odniesieniu do podmiotu skłonnego do ryzyka (b). Tutaj oczekiwana użyteczność korzyści jest większa od użyteczności jej wartości oczekiwanej. Koszt ponoszenia ryzyka mierzy się odcinkiem EV CE, gdzie CE interpretuje się jako korzyści w warunkach pewności przy uzyskanej oczekiwanej użyteczności dla w₁ i w₂.

Gdyby użyteczność oczekiwana gry była jednakowa dla asekuranta i ryzykanta (uczestniczą w identycznej grze i z założenia w obu przypadkach użyteczności z posiadania jednakowych wypłat są takie same) , to jednakowa byłaby także wartość oczekiwana z gry. Opisane osoby różnią się natomiast użytecznością z posiadania sumy odpowiadającej wartości oczekiwanej gry. W przypadku asekuranta jest ona wyższa niż w przypadku ryzykanta: U_A(EV)>U_R(EV).

U U_R

U_A

U_EVA

EU

U_EVR

0 EV wypłaty

Asekurant woli mieć na pewno sumę odpowiadającą wartości oczekiwanej gry niż grać rzeczywiście. W jego przypadku U_A(EV)>EU.

Ryzykant raczej zagra niż przyjmie oferowaną z pewnością kwotę równą wartości oczekiwanej gry. W jego przypadku oczekiwana użyteczność gry przewyższa użyteczność wartości oczekiwanej: U_R(EV)<EU.

Istnieje też kwota, której posiadanie na pewno daje decydentowi użyteczność równą użyteczności oczekiwanej gry. Jest to tzw. ekwiwalent pewności CE (certainty equivalent). Asekurant postrzega udział w grze jako nieprzyjemny. Należy wobec tego przypuszczać, że zechce on zapłacić za uniknięcie gry (CE_A<EV). Jest to doskonały kandydat na klienta instytucji ubezpieczeniowej. W przypadku ryzykanta jest odwrotnie: CE_R>EV. Pozbawienie możliwości podjęcia gry trzeba by mu zrekompensować, płacąc dodatkową sumę pieniędzy.

Malejąca krańcowa użyteczność pieniądza (Bernoulli)

użyteczność całkowita użyteczność całkowita

ΔU₂

ΔU₃

ΔU₂ ΔU₁

ΔU₁

(Δ U₁) > (ΔU₂)

0 ΔM₁ ΔM₂ ΔM₃ bogactwo 0 M₁ M* M₂ bogactwo

Skoro użyteczność krańcowa dochodu pieniężnego maleje, to utrata danej sumy pieniądza powoduje spadek użyteczności całkowitej, który jest większy od przyrostu użyteczności całkowitej spowodowanego dodatkowym dochodem takiej samej wielkości. Utrata kwoty M₁M* powoduje obniżenie się użyteczności całkowitej o ΔU₁, natomiast przyrost dochodu o kwotę M₂M*, równą M₁M*, podnosi użyteczność tylko o ΔU₂. Malejąca krańcowa użyteczność sprawia, że (ΔU₁) > (ΔU₂). Wartość bezwzględna straty jest większa od wartości bezwzględnej korzyści. Gra sprawiedliwa w kategoriach pieniężnych okazuje się niekorzystna w kategoriach użyteczności. Wygrana pewnej kwoty pozwoli na zakup jakiejś ilości dóbr luksusowych, przegrana zaś zmusi do zrezygnowania z zakupu znacznej ilości dóbr podstawowych. Właśnie dlatego ludzie unikają gier sprawiedliwych, czyli są niechętni ryzyku! Wyjątek może stanowić udział w okazjonalnych grach o niskich stawkach, prowadzonych dla czystej przyjemności. Gra zapewniająca równe szanse wygrania lub przegrania określonej kwoty pieniężnej nie jest grą uczciwą z punktu widzenia użyteczności.

Podejmowanie ryzyka zależy od dwóch czynników: uczucia przyjemności lub przykrości towarzyszącemu ryzyku.

W rzeczywistości są osoby, które mają różne preferencje w odniesieniu do ryzyka, zależnie od wielkości majątku, który posiadają.

U(w)

0 I II III wypłaty

Stosunek do ryzyka zależy od wielkości majątku konsumenta. Gdy nie jest bogaty (I), wówczas jest asekurantem. Przy większym majątku (II) staje się ryzykantem, ale po przekroczeniu kolejnego poziomu majątku (III) ponownie staje się asekurantem.

Zob. J. Hirshleifer: Investment Decision under Uncertainty - Choice-Theoretic Approaches, „The Quarterly Journal of Economics” vol. LXXIX, no.4/1965 i E. Smaga: Ryzyko i zwrot w inwestycjach, Fundacja Rozwoju Rachunkowości w Polsce, Warszawa 1995, s. 8-9.

Prof. ndzw. dr hab. Teresa Kamińska Mikroekonomia

1

OBSERWACJA

Zmiana definicji i/lub hipotez

Pojęcia, definicje, klasyfikacja

Uogólnienia informacji, czyli hipotezy (INDUKCJA)

Wyprowadzenie wniosków (DEDUKCJA)

Usunięcie błędu logicznego

Test empiryczny - konfrontacja z rzeczywistością

(KRYTYKA NAUKOWA)

Test logiczny poprawności wnioskowania

(KRYTYKA NAUKOWA)

Falsyfikacja

Brak falsyfikacji

Niespójność logiczna

Poprawność logiczna

Odrzucenie teorii i zastąpienie jej teorią konkurencyjną

Przejściowa wartość teorii

EU = p₁ U(w₁) + p₂ U(w₂) p₁ = EB p₂ = EA

Wartość oczekiwana (EV) tam, gdzie

Premia za podejmowanie ryzyka = CE EV Ekwiwalent pewności CE (0CE)

Koszt ponoszenia ryzyka = EV CE

∏_a

Ce

C_i

Ce

TR

C_i

TR

C_i

Ce

TR

∏_e

∏_a

∏_a

16 16 20 15

15 20 18 18

M

O

O

M

O

Politycy

Ekspansywność Bierność Restrykcyjność

---