00098483

258 III. FUNKCJE ZMIENNEJ ZESPOLONEJ

258 III. FUNKCJE ZMIENNEJ ZESPOLONEJ

f(t, nie ńinwjr. giljz warunki Cauchyego-Ricfnanna M spełnione lylku w punkcie /«    ⁰

Jeżeli funkcja.Az) jest holomorficzna w każdym punkcie obszaru D.to mówimy, ie jest holomorficzna w tym obszarze

J\z) = u(x,y)+M*,_>')

holomorficzną w pewnym obszarze D. Mamy więc

Holomorficznoić u, obszarze oznacza dokładnie to samo. co istnienie pochodnej w każdym punkcie lego obszaru Rozważmy funkcje

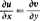
<111481

w każdym punkcie lego obszaru Załóżmy następnie, te funkcje u(.v, )j i «'(*. J'ż są klasy C¹ w obszarze O. Aczkolwiek fakt ten wynika z warunku. Że funkcja fis) jest holomorficzna w obszarze D — do sprawy tej wrócimy jeszcze w dalszym loku wykładu — jednakże obecnie przyjmujemy go z założenia.

Różniczkując obustronnie pierwsze z równań (11148) względem v, natomiast drugie względem y, otrzymamy

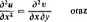
d³w _ d^łr óy¹ dydx

Stąd, na podstawie twierdzenia Schwarza o równości ciągłych pochodnych mieszanych drugiego rzędu, dostajemy

a więc część rzeczywista u(x, y) funkcji hol o' morfie znej w obs/aizc Djest funkcją harmoniczną w tym obszarze-W sposób analogiczny można udowodnić, że

a więc część urojona »(*,>•) funkcji holomorficznej w obszarze i> j e s t także funkcją harmoniczną w tym obszarze. Przypominamy, że funkcja harmoniczna jest z definicji klasy Cⁱ.

Def. Dwie funkcje harmoniczne u(x. y) i e(x,y) nazywamy sprzytonymi zc sobą, jeżeli spełniają układ róu-rum Cauchy'ego-Riemanna

Część rzeczywista u(x, y) i część urojona v(x, p) funkcji holomorficznej w pewnym obszarze, są zatem funkcjami harmonicznymi w tym obszarze, sprzężonymi ze sobą, Na odwrót, przypuśćmy, że dane są w pewnym obszarze dwie funkcje harmoniczne u(x, y) i ti(x, y), sprzężone ze sobą. Ponieważ są to funkcje klasy C², a zatem także klasy C¹, więc na podstawie warunku wystarczającego istnienia pochodnej stwierdzamy, żc./{:) = u(x, y)+jv(x, y) jest funkcją holomorficzną w rozważanym obszarze. Jeżeli więc dana jest para funkcji harmonicznych w pewnym obszarze, sprzężonych ze sobą, to jedna z nich (nie którakolwiek!) jest częścią rzeczywistą, natomiast druga jest częścią urojoną pewnej funkcji holomorficznej.

Przypuśćmy z kolei, że dana jest jedna funkcja u(x, y) harmoniczna w pewnym obszarze D. Dla uproszczenia założymy, że obszar ten jest wnętrzept prostokąta o bokach równoległych do osi układu. Będziemy poszukiwać funkcji /(z) holomorficznej w prostokącie D, dla której u(x, y) jest częścią rzeczywistą.

Jeżeli taka funkcja holomorficzna f(z) = u(x, y)+jv(x, y) istnieje, to jej część urojona v(x, y) spełnia układ równań (III.48), w których u(x, y) jest daną funkcją klasy C*. Układ taki rozwiązaliśmy względem t/(x, y) w tomie 2-gim (rozdz. II, p. 6) lego podręcznika. Otrzymaliśmy wówczas wzór, który po odpowiednim dostosowaniu do wprowadzonych obecnie oznaczeń jest następujący

(UL49)

C oznacza tu dowolną stałą (zespoloną), natomiast A₀(x₀; y₀) jest punktem dowolnie wybranym w prostokącie D. Funkcja w(a-, y) określona wzorem 011.49) spełnia zatem układ (111.48). Ponieważ pochodne ~~~ i występujące w tym układzie są klasy C¹ (bo funkcja ir(x, y) jest klasy C²), więc funkcja y) jest klasy C², a zatem także klasy C^l. Na podstawie warunku wystarczającego istnienia pochodnej wynika stąd, że funkcja j\z) — u(x,    p) jest holomorficzna

w prostokącie D-

Przykład. Znaleźć funkcję holomorficzną/(z), jeżeli dana jest jej część rzeczywista u(x, y) = = x²-y².

Mamy tu

- u,(ar, y) = 2y,    , y) = 2x

ponieważ funkcja x^I—y² jest harmoniczna w każdym prostokącie D, więc można przyjąć x<, = — y₀ = O.Z uwagi na wzór (111.49) otrzymamy wówczas

o(*. y) = | 2ydi+12 • Orf/+C «K*,y) - 2xy+C

A*) “ x*-y‘+i2xy+JC = (x+jy)^ł+JC

Stąd