042 043

42 Anna Borowska. Rafał Chaba

Ql=hffh    (2.44)

Ponieważ zależność (2.44) jest nieliniowa, zatem nieliniowe jest też równanie (2.42)

Po linearyzacji otrzymamy:

A~ = AQ,-AQ2 dt	(2.45)
AQ\ = vA/j	(2.46)
	(2.47)
^Qi V^2# fy) 4/i + fio 2^2gh ^	(2.48)
AQi - k\Af2 + k2Af{	(2.49)

gdzie:

*1 = V²^0    ~ flO ~

Podstawiamy zależności (2.46) i (2.49) do zależności (2.45) otrzymujemy:

A

dAh

dt

- vAf) - Aj A/₂ - k₂Ah

(2.50)

Ostatecznie równanie ruchu obiektu przyjmuje postać:

(2.51)

T^L + Ah = k₂Af_l-k_ĄAf₂

gdzie:

Al

^k2

Zmianę przekroju zaworów określamy równaniami:

A/, - -mfy

Afi - -7idx

Równanie ruchu zespołu rozdzielacz - siłownik hydrauliczny

7j — = AA - £

¹ dt

Równanie równowagi przesunięć dla dźwigni

£ - Z

a b

U.02)

(2.53

(2.54)

(2.55)

Przekształcając powyższe związki możemy wyznaczyć równanie ruchu układu w' następującej postaci:

/_ _\d²Ah ( _a\dAh (a .    ^

^r⁺h⁺M

= (k_i7tdT_x)A+[k_Ą![d~^x

AA =

(2.56)

Wykorzystując zasady budowania schematu blokowego układu automatyki, schemat układu można przedstawić jak na rys. 2.7

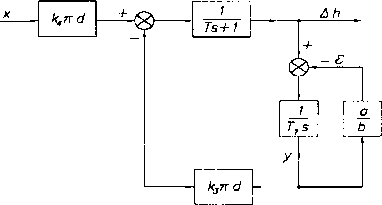
Rys. 2. 7. Schemat układu z rys. 2.6