034 035

34 Anna Borowska, Rafał Chaba

Wykonując transformatę Lapiace'a i eliminując prąd otrzymamy

10)

1 + sRC 1 + sRC

Zakładając £/_in.(0) = 0 znajdziemy transmitancję

_t 1

6(5) = -—--=

U_nv(3) \ + sT

(2.11)

gdzie: T = RC oznacza stałą czasową.

A zatem czwornik RC jest członem inercyjnym pierwszego rzędu o współczynniku wzmocnienia k — 1 .

2.2.3. Człon całkujący

Równanie i transmitancja idealnego członu całkującego wyrażają się wzo-

ram i

dy{t) di

ku{i)

(2.12)

S

(2.13)

gdzie: k - współczynnik wzmocnienia równy stosunkowi pochodnej sygnału wyjściowego do sygnału wejściowego w stanie ustalonym.

Przykładami członu całkującego idealnego są: kondensator idealny, siłownik hydrauliczny, zbiornik cieczy.

W rzeczywistości rzadko spotyka się idealne człony całkujące. Tylko przy pewny ch założeniach można przyjąć, że niektóre człony zachowują się jak całkujące. Takie człony przedstawia się przy pomocy całkowania z inercją. Równanie takiego członu jest następujące

_r£m₊m _{= iu(}„

dr dt

(2.J4)

gdzie:

k - współczynnik wzmocnienia. T- stała czasowa.

Transmitancja operatorowa członu całkującego z inercją ma postać

<2.15

G{s) =

k

s(l + sT)

Przykładem członu całkującego z inercją jest czwórnik RC przedstawiony na rys,2.3.

R

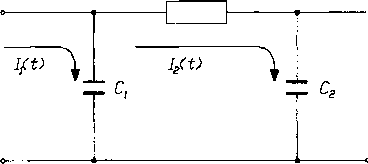
Rvx.2.3. Czwórnik RC

W układzie przedstawionym na ry s. 2.3 sygnałem wejściowym jest prąd /, (r) płynący przez kondensator Cj. a sygnałem wyjściowym - napięcie na kondensatorze C,. Napięcia na kondensatorach Cj i C₂ są następujące:

(2.16)

(2.17)

— J/, (r)dr = Rl, (/) + — J/j (r )dz

^L ' o    -o

\h(r)^dT

^C2 0

Po wykonaniu transformacji Laplace*a pr2y zerowych warunkach początkowych otrzymujemy transmitancję

G(s) =

/](s)    s(\ + sT)

gdzie: T = RC₂ oznacza stałą czasową.

(2.18)