044 045

44 Anna Borowska, Rafał Chaba

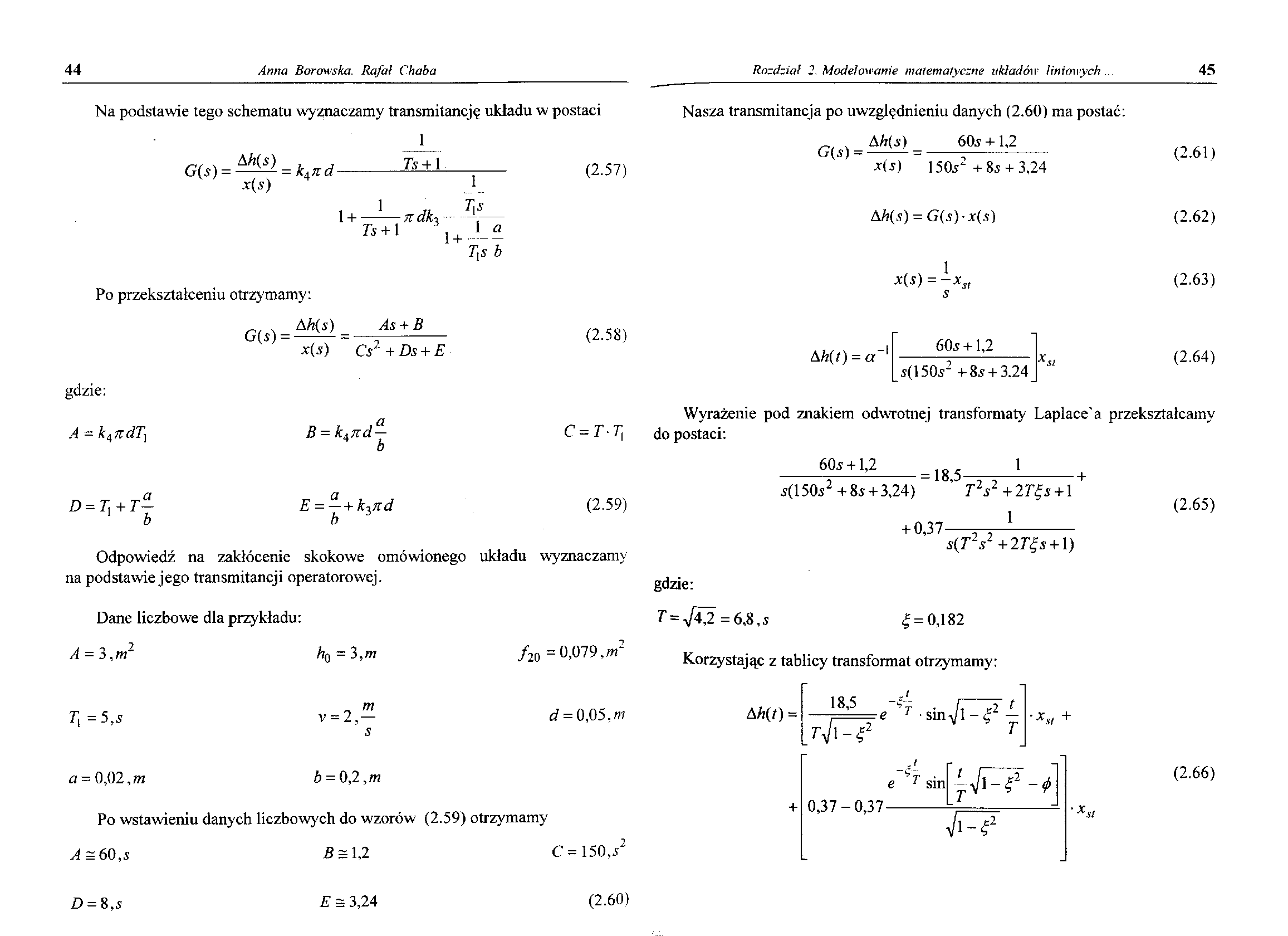
Na podstawie tego schematu wyznaczamy transmitancję układu w postaci

1

_G{s) = ^l = k_Axd~

x(s)

7s + l

(2.57)

i    ¹    T\^s

1 +-Ttdk-i ........

75 + 1    ³1 + J_fl

7]s b

Po przekształceniu otrzymamy:

	x &h(s) As + B Cr(s) = = *(•*) Cs^1 + Ds + E	(2.58)
gdzie:
A - kA7zdTJ	B = k47id — b
	E = — + k-,xd b ^3	(2.59)
Odpowiedź na zakłócenie skokowe omówionego na podstawie jego transmitancji operatorowej.		układu wyznaczamy
Dane liczbowe dla przykładu:
A = 3,m^2	h0 = 3,w	/20 = 0,079, m^2
T{ =5	o ^m v - 2,— s	d = 0,05,m
a - 0,02, m	ó = 0,2 ,m
Po wstawieniu danych liczbowych do wzorów (2.59) otrzymamy
A = 60,5	5 = 1,2	C = 150,5^2
<< 00 II Q	£ s 3,24	(2.60)

Nasza transmitancja po uwzględnieniu danych (2.60) ma postać: A h(s)    605 + 1,2

(2.61)

(2.62)

(2.63)

G(5) =

x(s) 1505" + 85 + 3,24 A h(s) = G(s) -jc(5)

x(s) = -x_st s

A h(t) = a'

605 + 1,2

5(1505" +85 + 3.24

(2.64)

Wyrażenie pod znakiem odwrotnej transformaty Laplace'a przekształcamy do postaci:

605 + 1,2

= 18,5-

5(1505² + 85 + 3,24)    ‘ ^ T²s² + ITĘs +1

(2.65)

+ 0,37

s(T²s² + 27^5 + 1)

gdzie:

=6,8,5    £ = 0,182

Korzystając z tablicy transformat otrzymamy: 18,5

AA(0 =

+

e ' sin

0,37-0,37

(2.66)