046 047

46 Anna Borowska. Rafał Chaba

gdzie:

¹ = arctg

Po wstawieniu wartości T i C, otrzymamy:

Ah(t) = x_s, [0,37 + 2.78<T⁰'⁰²⁶⁸' sinOJ 44/] +

(2-67)

:„[o.378e~°⁰²⁶⁸' sin[o,144/ -100°30']]

Wykres odpowiedzi na zakłócenie skokowe przedstawiono na rys. 2.8

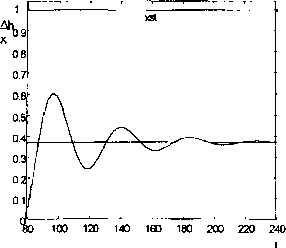
Rys. 2.8. Odpowiedź skokowa układit z rys. 2.6

Jak widać z wykresu zastosowany regulator nie kompensuje całkowicie zakłócenia działającego na obiekt. W stanie ustalonym istnieje odchylenie wielkości regulowanej od wartości zadanej Ah = 0,37 x _st.

Literatura:

1.    HOLEJKO D.. KOŚCIELNY W.. NIE WCZAS W. Zbiór zadań z podstaw automatyki. Warszawa. Wydawnictwo Politechniki Warszawskiej 1985

2.    PEŁCZEWSKI W. Teoria sterowania. Warszawa. WNT 1980

3.    STEFAŃSKI T. Teoria sterowania. Część 1. Skrypt nr 270. Kielce. Wydawnictwo Politechniki Świętokrzyskiej 1995

Rozdział 3

CHARAKTERYSTYKI CZASOWE I CZĘSTOTLIWOŚCIOWE

r

3.1. Wprowadzenie [1], [2]

I Transformacją operatorową G(s) obiektu liniowego ciągłego stacjonarnego nazywa się stosunek transformaty Laplace'a wielkości wyjściowej y(s) po transformaty Laplace’a wielkości wejściowej x(s) przy zerowych warunkach początkowych:

IV

(3.1)

G(,).*£) ₌ >2-

A ,

2*^ai^s

t=0

y^iJ){0) = 0, i/^(/)(0) = 0, / = 0,1.....w -1; j = 0,l,...,m- 1

| Transmitancja operatorowa jest zwykle ilorazem dwóch wielomianów | zmiennej zespolonej s:

(3.2)

|    ₌ ^bm s™ + K-\    +—+*i^s + ł>o _ M(s)

i    a_nsⁿ +a_n__]sⁿ~ⁱ +...+«] s + a₀ N(s)