055 2

Równania i nierówności wymierne

Założenia:

x ■+ 3 *6 x * —3 D=R\{-3}

Rozwiązanie:

Zapisujemy iloraz tych czynników jako ich iloczyn, przy założeniu, że mianownik jest różny od zera.

czyli

(v-2)(x + 3)<0

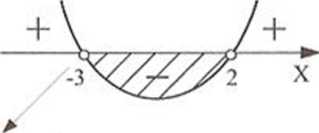
Teraz postępujemy tak. jak przy rozwiązywaniu nierówności wielomianowych.

Znajduję miejsca zerowe wyrażeń w nawiasie i rysuję wykres wielomianu.

Znajduję przedział (-3, 2).

bo .v * -3

Odpowiedź

-v e (-3,2)

ZADANIE 4

>0

2x + 5

a-7

Założenia:

.v - 7 * O x * 7

D = R\ {7}

Rozwiązanie:

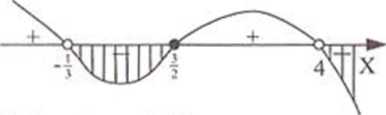
2.v + 5 x~ 7

>0o (2y + 5) (.v - 7) £ O i a * 7

Zastępujemy iloraz iloczynem, na podstawie twierdzenia (*).

Rozwiązuję zwykłą nierówność algebraiczną.

-v = -., = 7

\

-i

2

/

7

X

Znajduję jej rozwiązanie (-«c, - jjj u (7. +»).

Odpowiedz _

■y € (-cc, - -] u (7, +oc)

ZADANIE 5

<0

3 - 2x

(3 v + I )(.v - 4)

Założenie:

(3jv+ 1) • (x 4) < O czyli

3.v + I *0 i x - 4 * O stąd

3.v 't- —11, x 4

^x*~y ^x*⁴

ostatecznie

.v * - - i x* 4 d-r\{ ±4 Rozwiązanie:

3 - 2v

(3.v+ 1) (v - 4)

*^mr^xm-y*^mĄ

<, O o (3 - 2.v)(3.v + 1 )(x - 4) < 0

Korzystam z twierdzenia (*).

Rysuję pomocniczy wykres wielomianu.

Rysuję z dotu, bo współczynnik przy najwyższej potędze zmiennej jest ujemny.

Znajdujemy przedziały 3"

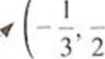
(4, -i- x) >

(h»    - mc nałoży

«l»il/ic<ł/inv

bo ■* nie lutcży do dziedziny

Ik> nic ic<l wyrzucana / dziedziny. :i znak

nierówności S

111