054

Równania i nierówności wymierne

NIERÓWNOŚCI WYMIERNE - przykładowe zadania

Definicja

Nierównością wymierną nazywamy nierówność postaci gdzie W(x) i P(x) są wielomianami i P(.v) £ 0.

Zanim przystąpimy do rozwiązywania zadań, zwróćmy uwagę na bardzo prostą, aczkolwiek przydatną zależność. Otóż znak ilorazu dwóch wyrażeń jest taki sam jak znak iloczynu tych samych wyrażeń. Przykład:

— znak ilorazu jest ujemny

( 6) • 2 znak iloczynu jest ujemny

Tutaj nic chodzi o wartości tych wyrażeń, a tylko o znak.

(*) Twierdzenie:

~~ > o H%x) ■ Q(x) > 0 i Q(x) * 0.

Twierdzenie to jest prawdziwe dla każdego rodzaju nierówności (<, <, >, >).

ZADANIE 1

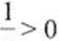
.v

Założenia:

{bo mianownik musi być różny od zera)

Zastępujemy iloraz ~ iloczynem, bo interesuje nas znak wyrażenia.

.v*0, D = R \ {0}

Rozwiązanie:

zatem

1 • a > 0 czyli .Y > 0

o ^x Odpowiedź A* € (0, +co) ZADANIE 2	Zgodnie z założeniem x* 0.
—^T^<° A* + 3 Założenia: * + 3* 0 stąd x & —3 D = R\{-3} Rozwiązanie 2 • (x + 3) < 0 1:2 x + 3 < 0	Zastępujemy iloraz iloczynem, interesuje nas znak wyrażenia.
A* < -3 Mm._^ A ^x bez -3, bo a* * -3 (założenie) Odpowiedź A' € (-CC, -3) ZADANIE 3	Tutaj rozwiązujemy nierówność liniową.
*-;<o A-+ 3

109