233

464 Rozwiązania i odpowiedzi

10.114. Funkcję można przedstawić w postaci y = i~ł cos 2x, skąd wnioskujemy _i okres jej wynosi 7t; oś Oy jest osią symetrii krzywej; tabelka (w przedziale <0, jr».’

X	...	0	...			±7t	...		...	n
y"	+	+	"T	0	-	-	-	0	+	+	+
y'	-	0	+	+	+	0	-	-	-	0	+
		1		3		2		3		1	■
y	\	m	/	2 P	/	M	\	2 P	\	m

10.115.    Funkcja jest określona dla wszystkich x; przy x=i(2k + l);r (k-0, 1,2,...) mamy y_min = i, a przy x = kn (k = 0, 1,2, ...) mamy y_max=l.

10.116.    Funkcja jest określona dla wszystkich xy\n+kn (k=0, ±1, +2,'...); przy x=^n+kn (k-0, ±1, ±2, ...) mamyy_max=l; asymptoty x=\n+kn (k=0, ±1, ±2,..,).

10.117.    y=l+sin (2x—^n), okres 7t; y' = 2 cos (2x—$n); tabelka (w przedziale <0, tt»:

X		0		5"		I*	...	n
y'	+	+	+	0	-	0	+	+	+
				2	\	0
y	S	2	y	M		m	y •	2	/
10.118. y	= i~ł cos (2x+$k), okres			n; y' = sin (2x + ^7t); tabelka (w przedziale					<0, tt»:
X		0	...	i*		f*		n	...
y'	+	+	+	0	-	0	+	_1_	+
				3		1
y	/	0	/	4 M	\	4 m	y	0	/

10.119. Okres 2rr; / = 4 sin (\x + sin Qn — |x); tabelka (w przedziale <0, 27t»:

X

...

0

...

I^71

...

17_ 12^U

...

2n

...

y

+

+

+

0

-

0

+

0

-

0

+

+

+

y

V2

y

3 2 M

\

-3 m

y

3 2 M

\

1 m

y

V2

/

10.120. y = cos x (1 —cos² x), okres 2k; y' = sin x (3 cos² x— 1); oś Oy jest osią symetf'¹ krzywej; tabelka (w przedziale <0, 2ir»:

X	...	0	...	a	...	TT —a	...	n		rt+a	...	2 n—a	...	2n	...
sin x	-	0	4-	+	+	+	+	0	-	-	-	-	-	0	4*
3 cos^2 x—1	+	+	4-	0	-	0	+	+	4-	0	-	0	+	+	+
y	-	0	+	0	-	0	+	0	-	0	+	0	-	0	+
y	\	0 m	/	|V3 M	\	ICO Li_	/	0 M	\	-iV3 m	/	|V3 M	\	0 m

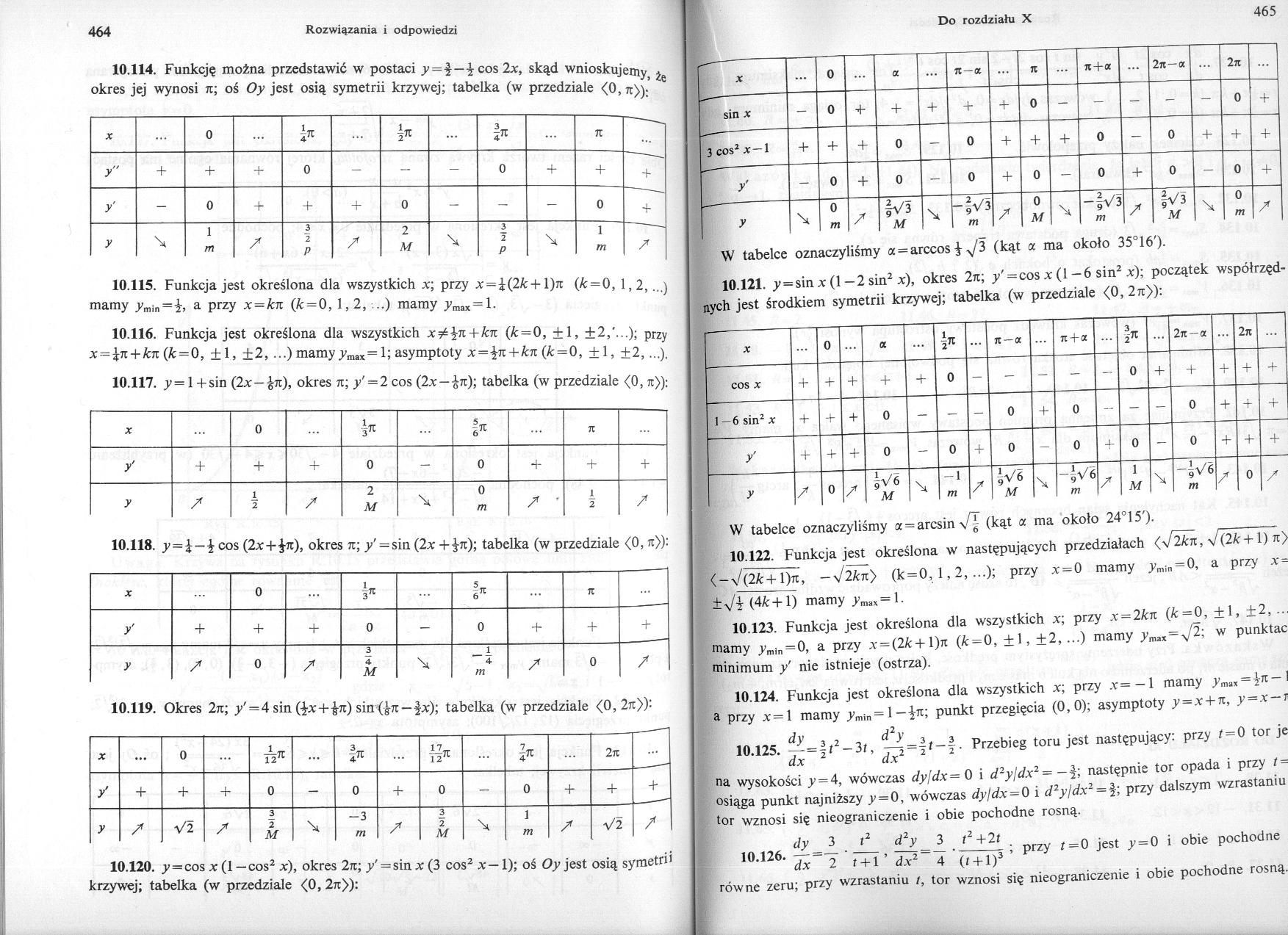
W tabelce oznaczyliśmy a = arccosJ_v/3 (kąt a ma około 35°16').

10.121. y=sinx(l — 2 sin² x), okres 2tc; y'=cos .v (1 -6 sin² x); początek współrzędnych jest środkiem symetrii krzywej; tabelka (w przedziale <0, 2jt»:

X		0	...	a	...	5*	...	n — a		Jt + a	...	ł*		2n —a	...	2n
COS X	+	+	+	+	4~	0	-	-	-	-	-	0	+	+	+	+	4-
1 —6 sin^2 x	+	+	+	0	-	-	-	0	+	0	-	-	-	0	+	4-	4“
y	+	4"	+	0	-	0		0	-	0	+	0	-	0	+	+	-f
y	/	0	/	|V6 M	\	-1 m		CM	\	m	y	1 M	\	-\y 6 m	/	0	/ /

W tabelce oznaczyliśmy a = arcsins/£ (kąt a ma około 24°15').

10.122. Funkcja jest określona w następujących przedziałach <%/2/czc, V(2k + 1) tt) < —V(2k+ l)jt, -yjlkn} (k = 0, 1,2,...); przy x=0 mamy y_min = 0, a przy x= ±Vł (4k+l) mamy y_max=l.

10.123. Funkcja jest określona dla wszystkich x; przy x — 2kn (k-0, ±1, ±2, ... mamy y_mi_n = 0, a przy x = (2k + l)n (k=0, ±1, ±2,...) mamy y_max=j2\ w punktac minimum y' nie istnieje (ostrza).

10.124. Funkcja jest określona dla wszystkich x; przy .v=-l mamy y_max=^—I a przy x= 1 mamy y_min=I—punkt przegięcia (0,0); asymptoty y=x + 7i, y=x—T

10.125. ~ =    _t    Przebieg toru jest następujący: przy r = 0 tor je

dx    dx²

na wysokości y — 4, wówczas dyjdx = 0 i d²y/dx² = — f; następnie tor opada i przy t = osiąga punkt najniższy y = 0, wówczas dyjdx = 0 i d²y/dx² = %; przy dalszym wzrastaniu tor wznosi się nieograniczenie i obie pochodne rosną.

dy 3 t² 10.126. —=- •—r

dx 2 t + 1

^d2i.

dx²

r+2t

, przy r=0 jest y = 0 i obie pochodne

(t + 1)³

równe zeru; przy wzrastaniu t, tor wznosi się nieograniczenie i obie pochodne rosną.