DSCN0532

100 3. Wytrzymałość przekładni walcowych

źnosci:

(3.12)

I 1 /1 I \    .. _r 2£, £₂

£    2 U, £2/    £,+£₂

Rozkład nacisku Hertza po szerokości paska styku jest eliptyczny, a maksymalna wartość w środku szerokości styku wynosi

Ph =

4 F_h

4_F^

nb

bE

F_h

(3.13)

n cb    nb V 32 F_bnQ(l — v²) \J 2ngb I—v²’[

Jeśli przyjmiemy dla stali v = 0,3 i wstawimy do wzoru (3.13), to otrzymamy

MM

p_H = /0,35£-^ = 0,418 ■■ I ^FH V    2ęb    V B^h

Po podniesieniu obu stron do kwadratu otrzymamy:

61

pń = 0,35 £

2ob

(3.13a)

(3.13b)

Jeżeli przyjmiemy za wartości stale £, F_h„ i b, to zauważymy, że kwadrat nacisków stykowych pf, zależy wprost proporcjonalnie od krzywizny zastępczej IIg, której wartość zmienia się na odcinku zazębienia AE. Ilustruje to rys. 3.10, na

I

1 mm 0 x i

r i? ^

\ I

odcinek przyporu

Lz

32$ X _

V \i

r 1 * L I

2 A

\ł \t

N

mm

rv>n. x —

T" Pi

X \ \\

/

/

1/1_

LicU

\

/

/

/ /

20- 0.1S-

\ \ %

\

/

/

> / /

V

/ - i

\

w,

A

A

\

s

/

15 “

V

-T ■

\

i

/

030-

\

)

1 1

><

10

i

<

1

1 4. !

\

DOS

/

1

; -n

\

1 1

‘V

orni_

/ /

1 1

\

Ni /

Pb

9 Ć

0 s M_r

e m podziotko dla odcinka

i i

Rys. 3.10. Teoretyczny przebieg nacisków itykowych wzdłuż odcinka przyporu AE (przykład dla z,

- 27, z₂ - 43. m - 3)

którym linią przerywaną przedstawiono przykładowo zmianę krzywizny zastępczej 1 /o zębów ewolwenlowych. Najmniejsza krzywizna występuje w środku S linii zazębienia N_t N₂. Dla przełożenia u > 1 odcinek przyporu AE przyjrpuje położenie niesymetryczne względem środka S i to tym bardziej, im większe jest przełożenie. W związku z tym największe naciski wystąpią na odcinku wzębienia g_f = AC, mniejsze zaś na odcinku wyzębienia g_m = CE. W punktach B i D występuje zmiana przyporu z dwuparowego w jednoparowy (jednej pary zębów) i związana z tym skokowa zmiana obciążenia zębów, teoretycznie z 0,5F_fcn do F_btl. Podobnie, wystąpi skokowa zmiana wartości kwadratu nacisku stykowego p„ zgodnie ze skokiem wartości siły oraz jego dalsza monoloniczna zmiana zgodnie z przebiegiem zastępczej krzywizny, co przedstawiono na rys. 3.10 linią ciągłą grubą.

Łatwo można wyznaczyć nacisk stykowy w biegunie zazębienia C. Promienie krzywizny zębów, równe promieniom ewolwent dla tego punktu, wynoszą:

6ic = — sina,.,

Qic = — sinz„.

(3-14)

a krzywizna zastępcza:

u sina_w

d_w

(3.15)

Uwaga. W zazębieniu wewnętrznym przyjmuje się umownie dla średnicy d_wl oraz innych parametrów kola wewnętrznego znak minus. Szczegóły podane są w pkt. 11 i 16.

Po wstawieniu wyrażenia (3.15) do wzoru (3.13a) otrzymamy wzór na obliczenie nacisku stykowego w biegunie zazębienia:

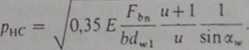
(3.16)

Wprowadzając [wzór (3.3)]

F

27j

COS

</„, cosa_w

otrzymujemy

(3.17)

lub