DSCN0545

124 3. Wytrzymałość przekładni walcowych

na niższe kaskady i kończy się naprzeciw szczytu bardziej oddalonego od osi czasu niż szczyt początku strugi, tzn. wówczas gdy na swojej drodze czasu napotka minimum (maksimum) niższe (wyższe) niż początkowe. Spływająca struga zatrzymuje się też wówczas, gdy na swojej drodze napotka strumień spływający z wyższej kaskady. Tak więc na rys. 3.22 pierwsza struga rozpoczynająca się od

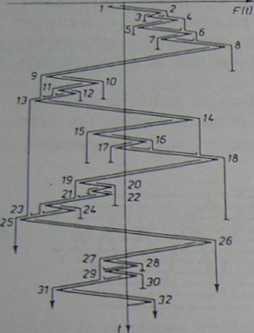
Rys. 3.22. Aproksymacja przebiegu obciążenia metodą obrysu (rain Dow counting method)

lokalnego minimum / kończy się naprzeciw szczytu 9, gdyż stanowi on minimum bardziej ujemne niż minimum początku strugi /. Pólcykl / — 8 jest pierwszym ze zliczanych pólcykli. Następny jest pólcykl 2 — 3, 4 — 5, 6 — 7 itd. Strumień biorący początek w wierzchołku 3 zatrzymuje się pod szczytem 2 i jest uzupełnieniem do pełnego cyklu dla poprzedzającego go półcyklu 2 — 3. W ten sposób nie pomija się żadnego fragmentu rzeczywistego przebiegu i każdy fragment jest zliczany tylko jeden raz. Największy pólcykl zawarty jest pomiędzy najbardziej dodatnim maksimum a najbardziej ujemnym minimum, a więc pomiędzy punkta mi 8 i 25 na podanej ilustracji.

W odniesieniu do przekładni zębatych układu napędowego autobusu komun kacji miejskiej, badania analityczne i eksploatacyjne [213 wykazały, że metod obrysu jest bardziej odpowiednia od innych do zastępowania losowego przebiej obciążenia ekwiwalentnymi fragmentami przebiegu harmonicznego.

Jeżeli wartości średnie obciążeń rzeczywistych podlegają też większym wał niom, to należy przeprowadzić aproksymację dwuparametrową, w której okre się nie tylko wartość amplitud a_a% ale także wartości średnie <r_m. Następn etapem jest transformacja amplitud ze względu na wartość średnią i sprowadzt widma obciążeń do przebiegu sinusoidalnego o zerowej wartości średniej. Kórz;

się przy tym z różnych tablic korelacyjnych lub odpowiednich wzorów podawanych w literaturze specjalistycznej, np. w pracach [233 I [55].

Należy jeszcze raz podkreślić, że aproksymowane widmo obciążeń jest jedynie przybliżonym i uproszczonym według przyjętych reguł zapisem analizowanego przebiegu obciążeń. Daje ono jednak, w połączeniu z odpowiednio dobraną hipotezą kumulacji uszkodzeń, możliwość dokładniejszego prognozowania eksploatacyjnej trwałości niż opieranie się tylko na obciążeniu nominalnym i współczynnikach ujmujących zgrubnie wpływ różnych czynników i oddziaływań. Postępowanie jest żmudne i czasochłonne i daje zadowalające wyniki wówczas, gdy dysponuje się już odpowiednimi informacjami z badań eksploatacyjnych i zmęczeniowych.

3.15. Hipotezy kumulacji uszkodzeń i eksploatacyjna trwałość zmęczeniowa

W literaturze technicznej, np. w pracy [SS], opisano wiele hipotez kumulacji uszkodzeń zmęczeniowych. Tutaj przypomnimy dwie wybrane, a mianowicie: hipotezę Palmgrena-Minera, która stała się hipotezą wyjściową dla wielu innych modyfikowanych hipotez, i hipotezę Serensena-Kogajewa, która w zastosowaniu do obliczeń trwałości kół zębatych może być bardziej przydatna od innych.

3.15.1. Hipoteza Palmgrena-Minera

Hipoteza Palmgrena-Minera zakłada, że w czasie każdego cyklu zmiany obciążenia próbki lub elementu część pracy przenoszonej przez ten element zostaje zatrzymana w jego tworzywie i narastając pozostawia ślad (objawia się) w postaci uszkodzenia struktury. Uszkodzenia te, kumulując się, powodują wyczerpywanie się nośności elementu, tj. zdatności przenoszenia obciążenia zmiennego.

Dla elementu nowego przyjmuje się jego pełną nośność równą jedności. Pochłoniętą i zatrzymaną przez tworzywo pracę w warunkach występowania naprężeń a przy n cyklach zmian obciążeń oznaczymy symbolem w. Z kolei wielkimi literami oznaczymy odpowiadające temu naprężeniu wartości graniczne, a więc graniczną liczbę cykli N i graniczną wartość pracy W, przy których następuje zniszczenie próbki lub elementu. W teorii Palmgrena-Minera zakłada się, że każdy zbiór cykli obciążeń n₍ przy naprężeniach większych od granicy zmęczenia a_K wyczerpuje nośność, czyli powoduje jej obniżenie, proporcjonalnie do ilorazu:

(3.52)

Wj    ;?,•

W? “ty*

gdzie w, jest pracą pochłoniętą przez tworzywo próbki w /i, cyklach przy naprężeniach <T,, fV, - pracą prowadzącą do zniszczenia próbki przy a_t, n_t - liczbą cykli