DSCN0535

104 3. Wytrzymałość przekładni walcowych

lizowane we wzorze (3.22). które są brane szczegółowo pod uwagę w operacyjnych metodach obliczeń sprawdzających. Przedstawiona tu zasada jest jednak zawsze zachowana w różnych metodach szczegółowych.

Należy tu podkreślić, że z warunku nacisku międzyzębnego (a więc ze względu na pitting) wynikają potrzebne wymiary zębnika hd_wl lub potrzebna umowna objętość zębnika 6</i,. występująca we wzorze (3.17a). Wielkość samych zębów, a konkretnie modułu, nie ma tu jakiegoś bezpośrednio wyraźnego wpływu, chociaż jest decydująca w obliczeniach zębów na złamanie, przy wyznaczaniu naprężeń gnących w stopie zęba.

Wartości graniczne nacisków stykowych lub naprężeń stykowych wyznacza się w eksperymentalnych badaniach kół zębatych i podaje się w tablicach i na wykresach zmęczeniowych.

3.5. Zasady wyznaczania naprężeń w podstawie zęba

Zagadnienie naprężeń w podstawie zęba rozważymy także na przykładzie zębów prostych. Ząb wystający z wieńca koła potraktujemy w uproszczeniu jak belkę utwierdzoną i obciążoną silami statycznymi. Największe naprężenie w podstawie zęba wystąpi wówczas, gdy pelpa sila będzie przyłożona możliwie daleko od przekroju niebezpiecznego, a więc u wierzchołka zęba. Przyjmiemy, że przekrój niebezpieczny jest płaski, wyznaczony przez punkty styczności paraboli wpisanej w obrys zęba. W uproszczeniu można przyjąć przekrój niebezpieczny wyznaczony przez punkty styczności linii prostych, nachylonych do osi zęba pod kątem 30° (rys. 3.11). Taki właśnie model obciążenia przyjęty do naszych wstępnych rozważań przedstawiono na rys. 3.1 la. Siła F_bm działająca wzdłuż linii przyporu wywołuje w podstawie zęba naprężenia złożone z gnących, ściskających i tnących. Aby obliczyć naprężenia składowe, rozłożymy siłę normalną F_bn na dwie składowe: F_e, działającą w kierunku osi zęba i powodującą jego ściskanie, oraz F_t, działającą prostopadle do osi zęba, co powoduje jego zginanie i ścinanie. Nominalne naprężenia składowe w podstawię zęba o grubości s_F i długości b wynoszą: i gnące

(3.24)

M_g _ 6F_t h_F _ 6F_hn h_F    6Fh_F cosa_F

W_% bs_F bsl ^h bs_F cos <x_w ’

— ściskające

— tnące

F_c    F sinoc_F

' bs_F    bs_F cos ot*’

H    F cos cc_F

bs_F    bs_F cos a_w

(3.25)

(3.26)

W ogólnym przypadku złożonego stanu naprężeń sumujemy naprężenia normalne i styczne według uznanych hipotez. W naszym przypadku należałoby zastosować np. wzór:

a_s =    (3.27)

Wyznaczenie naprężenia złożonego w podstawie zęba nie jest jednak lak proste i jednoznaczne, gdyż:

ł) u podstawy zęba występuje karb, powodujący spiętrzenie naprężeń o różnym nasileniu w odniesieniu do naprężeń gnących, ściskających i tnących;

2) maksimum naprężeń składowych nie występuje dla nich wszystkich w tym samym miejscu, w szczególności wartość naprężenia tnącego na samej powierzchni spada do zera, gdyż płaszczyzna działania siły F_f jest przesunięta w stosunku do rozpatrywanego przekroju ścinanego.

Oprócz tego różnie przyjmowany jest sam model obciążenia zęba, co będzie naświetlone w pkt. 3.6. Obecnie chodzi o przedstawienie fizykalnej zasady wyznaczania naprężenia i doprowadzenie wzoru do postaci dominującej w rozlicznych metodach:

<*F

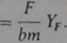
Rys. 3.11. Modele do wyznaczenia naprężeń w podstawie zęba: a) siła przyłożona u wierzchołka zęba, przekrój niebezpieczny płaski, wyznaczony punktami styczności paraboli wpisanej w obrys zęba lub punktami styczności linii prostych, nachylonych do osi zęba pod kątem 30*. b) siła przyłożona w skrajnym punkcie jednoparowego zazębienia, przekrój niebezpieczny plaski tak jak w pkt. a

(3.28)

Naprężenie w podstawie zęba traktowane jest tutaj umownie i oznaczone najczęściej symbolem a_F, a nie jak we wzorze (3.27) symbolem a_t.

W obecnych naszych rozważaniach przyjmiemy klasyczny sposób sumowania