lista10bp

Lista lObp

1. Wyznaczyć całkę funkcji wymiernej

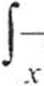
- +.Y-12

2.v +1

dx

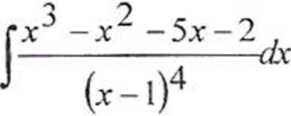
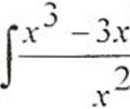
² + 5x-9 , -dx

-3x

I

1

dx

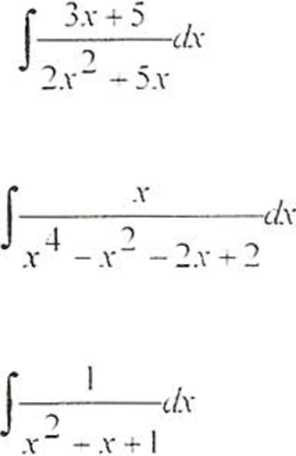
2. Wyznaczyć całkę funkcji trygonometrycznych

1

J

I

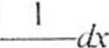
COS A

-»

cos^J ,v dx

*ł

sin a* cos

a dx

i

i

5 + sin .y + 2 cos x

-dx

J tg .v d\

I

I

sin .y

dx

i

0 + 4 cos A

■d\

COS A

9

sin“ A + 8sin a + 10

-d\

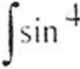
A COs “ A d.X

3.    Rozwinąć funkcje na szereg Maclaurina

__r-    X    ~>

f(x) = e    f(x) =- fiXI = cos^- .Y

3-.y

4.    Rozwinąć w szereg Taylora funkcje

/(.y) = sin .y - .y cos.y    w otoczeniu punktu x = 0

I    ,

/(.y) = —    w otoczeniu punktu    x = j

x

/ZA

/(.y) = sin -—    w otoczeniu punktu    .y = 2