M a t e m a t k a k r o k p o k r o k u I Page 01 (8)

FM PDF To Image Converter Pro

Unregistered version www.fm-pdf.com

Koło i okrąg są następnymi zagadnieniami, w których stosujemy uproszczenia - promieniem kola (okręgu) nazywamy zarówno liczbę, jak i odpowiedni odcinek. W tych przypadkach stosunkowo łatwo ustalić, kiedy chodzi o liczbę określającą długość odcinka, a kiedy o odcinek. Zwracamy uwagę na to. że kolo wyznacza okrąg i odwrotnie. Nie tłumacząc pojęcia wnętrza i brzegu figury, mówimy, że okrąg jest brzegiem odpowiedniego kola, zaś koło bez okręgu jest jego w nętrzem.

Warto trochę miejsca przeznaczyć na omówienie położenia prostej i okręgu. Łatwo stwierdzić, że możliwe są trzy położenia:

1 ° prosta jest rozłączna z okręgiem,

2° prosta ma dokładnie jeden punkt wspólny z okręgiem,

3° prosta ma dwa punkty wspólne z okręgiem.

Przypadki te się wy kluczają, również analityczne opisy tych przypadków też się wykluczają. Możemy zatem powiedzieć, że mamy do czynienia z zamkniętym układem twierdzeń. Założenia są wykluczające się i wyczerpują wszystkie możliwości. Również tezy się wykluczają i wyczerpują wszystkie możliwości. W takim przypadku wystarczy udowodnić jedną serię twierdzeń, gdyż twierdzenia odwrotne są też prawdziwe i nie wymagają dowodu. Nie namawiamy, aby twierdzenia te dowodzić w klasie. Sygnalizujemy tylko, że nie są potrzebne dowody twierdzeń odwrotnych.

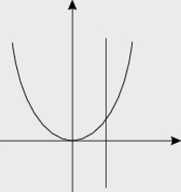
Mówiąc o prostej stycznej do okręgu, z premedytacją nie definiujemy stycznej do krzywej.

Definicja ta jest bardzo skomplikowana i wymaga używania pojęć z matematyki wyższej (pojęcie granicy ciągu, granicy ciągu punktów' płaszczyzny - topologia przestrzeni R") i lepiej nic na ten temat nie mów ić, aby nie wprowadzać w' błąd określeniem stycznej jako prostej mającej dokładnie jeden punkt w spólny z krzywą. W przypadku paraboli takie wyjaśnienie styczności jest fałszem (patrz rysunek obok).

Realizując zagadnienia związane z położeniem dwóch okręgów (kół), rów nież omawiamy zamknięty (zupełny) układ twierdzeń. W sformułowaniach dotyczących tego zagadnienia celowo używamy terminów okręgi i koła w tych miejscach, w których jest to wygodne. Mówiąc o okręgach stycznych, lepiej stosować termin: okręgi. Gdy koła są rozłączne,