00098513

314 III. FUNKCJE ZMIENNEJ ZESPOLONEJ

Przed sformułowaniem drugiego wniosku z twierdzenia podstawowego Cau-chy’ego, wprowadzimy następujące oznaczenia: D i D, oznaczają obszary jedno* spójne, przy czym D, c D, symbole C, i C₂ oznaczają zaś kawałkami gładkie krzywe • Jordanu usytuowane na płaszczyźnie zespolonej tak, te C_t e D, C, leży wewnątrz Cj i O, leży wewnątrz C, (ryt 111.36).

314 III. FUNKCJE ZMIENNEJ ZESPOLONEJ

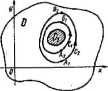
Rys. 111.36

DD_t,^ an.ui) j

Wniosek 2. Jeżeli funkcja f[ż) jest holpmorficzna w fyf(2)dz = fyf(z)dz

'Mffl

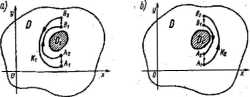
Rys ID.37    „(I

W celu uzasadniania (ega wniosku, rozważmy dwie kawałkami gładkie krzywe '"“''a Jf, c D-D, oraz *, ^c D-D„ przedstawione na rys. nt.37a, b. Związek tych krzywych t wynu C, i C, jest widneany. Na mocy twierdzenia podstawowego Cauchy ego mamy ^ /(z)dr — 0 oraz    - 0

I. TWIERDZENIE PODSTAWOWE CAUCHYEGO

315

(por. rył. mr7», b). Z uwagi na równości CU1.132) mamy więc

0 = ^ /(z)*+^/(x)rfr =    /(r)*+ jy f(i)dx - - £./(x)<fc+

skąd dostajemy ostatecznie równość (III. 13!), sad.

Uwaga. Zauważmy, że dowód jaki przeprowadziliśmy (nożna pozostawić bez z jeżeli w sformułowaniu wniosku zamiast obszaru domkniętego D_l wystąpi punkt Za e holomorficzności funkcji/(z) jssl w tym przypadku obszar /> bez punktu z«. Jest to obszar dmtspójay.

Dla ilustracji lego wniosku powróćmy do równości (111.121) w przypadku n > 1. Funkcja podcałkowa

jest holomorficzna na calćj płaszczyźnie z wyjątkiem punktu z_u. Zgodnie ze wzorem (IH.12I), całka

&

nie zależy od g, co stanowi zapowiedzianą ilustrację równości (111.131).

Trzeci i ostatki wniosek z twierdzenia podstawowego Cauchy’ego, który obecnie podamy, poprzedzimy — podobnie jak poprzedni — wprowadzeniem oznaczeń. Przypuśćmy zatem, że O oznacza obszar jednospójny orazżez_k eZ>, diak — 1,2, Niech C oznacza kawałkami gładką krzywą Jordana położoną w obszarze D i zawierającą punkty z*, k 1,2,...,«, w swym wnętrzu, symbole A* niech oznaczają okręgi o środkach z_lt k= 1,2, i wspólnym promieniu p tak małym, żeby żadne dwa z tych okręgów nie miały wspólnego punktu i żeby każdy z tych okręgów leżał wewnątrz krzywej C (rys. III.38).    /- •

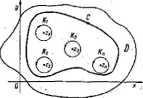
Wniosek 3. Jeżeli funkcja/(z)jest holomorficzna w z wyjątkiem punktów z,, z,,.... z;, to