0290

291

§ 5. Przybliżone rozwiązywanie równań

Ponieważ/(3) ma właśnie taki sam znak jak i /"(x), przeto na mocy wzoru (8):

x'i

/(3) ^ 0,43136... rW-0,91141...

-0,473... ;

0,0199

weźmy x\ = 3— 0,47 = 2,53. Mamy /(*j)=/(2,53) = 0,019894..., a więc x[ —-<0,03. Mamy

dalej    °>⁷

x'₂=2,53 —

/(2,53) /'(2,53)

= 2,53

0,019894..

0^83741...

=2,53-0,02375... ;

weźmy x₂ — 2,53—0,0237 = 2,5063 i oszacujmy błąd za pomocą nierówności

(6):

/(2,5063)=0,000096...,

*2-£<

0,000096...

<V7

<0,0002 ,

tzn. 2,5061 <(<2,5063. Tym razem mamy już z żądaną dokładnością * = 2,5062±0,0001 .

(W rzeczywistości 2,5062 jest przybliżoną wartością £ z nadwyżką, gdyż /(2,5062)>0).

3) Wróćmy do równania

2^x=4x,

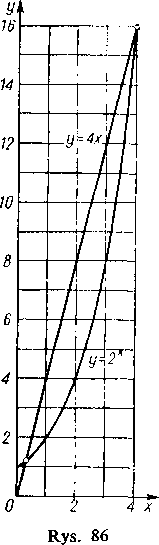
o którym mówiliśmy już w ustępie 81. Widzieliśmy tam, że między 0 a 0,5 zawarty jest pierwiastek tego równania. Fakt ten można byłoby zauważyć tak samo łatwo z wykresów funkcji y=2* i y=4x. Na rysunku 86 widać wyraźnie, że krzywe te, oprócz punktu o odciętej 4 mają jeszcze jeden punkt przecięcia o odciętej { między 0 a 0,5. Obliczymy ten pierwiastek z dokładnością do 0,00001.

Dla 0<x<0,5 mamy

f(x)=2*-4x,    /' (x) = 2^xln 2- 4<0 ,    /"(x)=2*(ln2)²>0

(przypadek II). Tutaj m=4 — ^ln 2>3, M=^J 2(ln2)²<0,7, A//2m <0,12. Ponieważ /(0) = 1 ma ten sam znak co i f"(x), zaczynamy od a = 0. Na mocy (6) błąd tej wartości przybliżonej jest mniejszy od 3, a wtedy na mocy (11) można z góry oszacować błąd

S—xi <0,12-, <0,014.

Dlatego obliczoną według wzoru (8 *) wartość

1

1

ln2—4 3,306852.

=0,30...

zaokrąglimy do dwóch znaków dziesiętnych: xj = 0,30. Korzystając z wartości /(0,30) = 0,031144..., możemy z nierówności (6) dokładniej oszacować błąd

<0,011 ,

0,031144...

<---

3

a wtedy na mocy (11):

(~x₂ <0,12 - 0,000121 <0,000015 ,