oblicz metod gaussa

ĆWICZENIA Z ALGEBRY LINIOWEJ I GEOMETRII ANALITYCZNEJ

Zestaw IV : układy równań liniowych

1. Rozwiązać układy równań metodą Cramera:

x T 2 y T 3 z — 1 2x + 3y + z = 3 3x T y T 2z — 2

x + 2y — z = 1 a)<j 3x + y + z = 2 x — 5z =0

x — 2y + 3z = —7

3x + y +    — 5    , c)

2x -f 5y + z = 18 2. Stosując wzory Cramera obliczyć niewiadomą y z układu równań:

r + y + 2: + t =	0		r T 3y T 32: T 3t — 1		3x 4- 7y + 2z 4- 4t	= 0
y 4- z 4-t = x 4- 2y + 3z =	1 2 ’	6) <	3x + y 4- 3z + 3i — 1 3x 4- 3y + z + 3t = 1 ’	c) <	2 y + z x + 4 y 4- z	- 0 = 1 ^5
y + 2z + 3t =	-2		k 3x + 3y 4- 3z +1 — 1		k 3x 4-3y 4- 2z	= 0

a)

3. Dla jakich wartości parametru m E i?, układ jest układem Cramera:

	3 X 4r z = 1	6x + 42: = 2
a) <	mr — my + 2: = —m , 6) <	r + my -f z = 3 , c) <
	x + my + 2: = 3	mrr — my + z = —m

6x + my -h 4z = 4m 3r + |/ + 2z = rn 6mx 4- v 4- 4z = 4

4. Rozwiązać układy równań metodą eliminacji Gaussa:

aj

T --//    ■ '

3r + z

^U)

-i-

*.L ~j ć/.

x 4- 5y + 4^

.< c y i z — l x 4- y — z + t

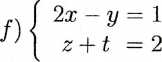
e) <

d)<

x + y 4- 2: + t 2x T 2y T z T t 3x 4- 2y + 3z + 2t 6x + 4y + 3z 4- 2t

x — 2 y    +3s+t = 1

2x — 3y 4- z 4-3s Ą-2t — 3 x — 2y 4- z 4- 3s — t = 1 y + 3s + 5t = 0 x — 2 y    + 55 + St = — 1

a: — y + 2: =0		a: + y + z — 2
x 4-y — z =0	' 3x + 2y-2z = 3	1 II 0
x 4- 3y — 32: = 0 , ń) <	3x + y + 2z = 1 , i) <	y-z = -3
! 1! 0	2x + 3y + 2z = 5	a;-y = 1
x 4-y 4- z = 0		0 II 1 1 H _/

3)