0134

IX. Całka oznaczona
i analogicznie
(8)

b—a
6
W ten sposób dochodzimy wreszcie do wzoru przybliżonego
W ostatnim wzorze pole figury pod krzywą jest zastąpione przez pole figury ograniczonej od góry zwykłą parabolą (o osi pionowej), przechodzącą przez trzy punkty krzywej: dwa skrajne i środkowy.
Gdy zwiększa się stopień k wielomianu interpolacyjnego, tzn. prowadzi się parabolę (3) przez coraz większą liczbę punktów krzywej, można liczyć na uzyskanie większej dokładności. Jednakże w praktyce dogodniejsza jest inna droga, oparta na połączeniu interpolacji parabolicznej z rozdrabnianiem przedziału.
324. Rozdrobnienie przedziału całkowania. Przy obliczeniu całki J /(,r) dx można postąpić na-
«
stępująco. Rozbijamy najpierw przedział <a, ó> na n równych części
*„> (*o — a, x. = b)
(9)
J f(x)dx+ f f{x)dx+ ... + J f(x) dx .
Teraz do każdego z przedziałów zastosujemy interpolację paraboliczną, tzn. będziemy obliczali całkę (9) za pomocą jednego z wzorów przybliżonych (4), (6), (8).
Łatwo się przekonać, że stosując wzory (4) lub (6) otrzymamy w ten sposób znane nam już wzory prostokątów i trapezów (1) i (2).
Zastosujemy teraz do obliczania całek (9) wzór (8), przy czym oznaczamy jak wyżej
f(x,) = y,,
"* *1+1/2 > /(*l+l/2) “ y<+l/2 •
Otrzymujemy
X,+Xu.t
2

J' f(x) dx * ^^-(yi+4ym+yt),

Na koniec dodając stronami te równości otrzymujemy wzór
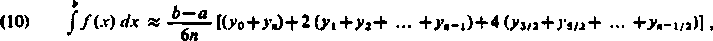
Wyszukiwarka
Podobne podstrony:
114 IX. Całka oznaczona W analogiczny sposób sprawdza się pozostałe wzory. 3) Znaleźć całki n/2
67971 skanowanie0026 (21) opowieści o dziejach, bo w ten sposób dochodzi się do prawdy. „Niczem jedn
ucznia. W ten sposób dochodzi Herbart do przedstawienia struktury procesu nauczania, na której oparl
122 IX. Całka oznaczona a zatem Z drugiej strony, 2a (a+b)—(a~b) sin20 __dO_ (a+ó)+(a-*)sin20
96 IX. Całka oznaczona więc analogicznie w przedziale <at, bf> możemy znaleźć podprzedział
112 IX. Całka oznaczona napisać analogiczny wzór dla całek oznaczonych (5) J f(x)
82 IX. Całka oznaczona W każdym z odcinków <*,, x,+i> wybierzmy dowolny punkt x = Ę, (l): X
84 IX. Całka oznaczona Sumy Darboux mają następujące, proste własności: Własność 1. Jeśli do
86 IX. Całka oznaczona e > 0 można znaleźć taką liczbę ó > 0, że skoro tylko X < 5 (tzn. je
88 IX. Całka oznaczona Dla pierwszej sumy, podobnie jak w poprzednim twierdzeniu, mamy < e(b-a).
90 IX. Całka oznaczona Łatwo zauważyć że nie wywoła to zmiany wartości samej całki. Wynika to stąd,
92 IX. Całka oznaczona Przyjmijmy teraz i _ « 2m Q ’ gdzie 12 oznacza oscylację
94 IX. Całka oznaczona 303. Własności całek wyrażające się równościami. Podamy dalsze własności
98 IX. Całka oznaczona 10“ Uogólnione twierdzenie o wartości średniej. Zakładamy, że 1) funkcje /(x)
100 IX. Całka oznaczona Ciągłość funkcji fU) w punkcie t — x oznacza, że do każdej liczby e > 0 m
102 IX. Całka oznaczona — jak to widać z założeń o funkcji /(x) są nieujemne, więc zastępując
więcej podobnych podstron