164

A HibUl. IM1U.1 ,Vv»i    r.», r ), buui :uO

ISBN D4H1II ł-7. © by »N TOS >*}

164

5 SYMETRIA CZĄSTECZEK

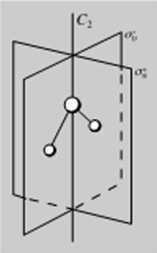
R»x. 5.5. Cząsteczka IIjO i jej elementy *y inclni Cj. o,' uraz o". Ciupa punkknwa C>._ Wszyukie jądra atomowe lezą im płaszczyźnie

ff,'

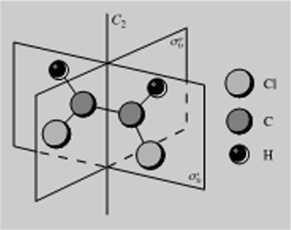
Rys. 5.6. Cząsteczka di CiHA oraz jej elementy symetrii Gni|v» punktowi 0;, Wszystkie jądra atomowe lezą iu płaszczyźnie a'_v

leży la oś Do grupy C_:, (cząsteczka H»0. rys. 5 5. oraz cząsteczka ds-CjIIjCIj widoczna na rys. 5.6) należy operacja C>. operacja Cj = F., ale ponadto także odbicie w płaszczyźnie a\. Można teraz wykazać, żc obrót Cj i odbicie w płaszczyźnie er' jest równoznaczne z wykonaniem tylko jednej operacji, a mianowicie odbicia w płaszczyźnie er" prostopadłej do płaszczyzny a[,. Obydwie płaszczyzny przecinają się wzdłuż osi C>. W rezultacie punktowa grupa symetrii obejmuje operacje Cj. E. er' oraz a". Można podobnie wykazać, żc grupie C», odpowiadają operacje symetrii F.. C_:„ C(. er,', er," oraz er,'". Przykładem cząsteczki o symetrii C», jest cząsteczka amoniaku, która ma strukturę piramidy trygonałnęj przedstawioną na rys. 5.7. Na grupę punktową Ci,, składają się następujące operacje symetrii: E. C,. C, (= Cj). Cj oraz odbicie w 4 płaszczyznach symetrii tworzących ze sobą kąty 45 Przykładem cząsteczki o symetrii C«, jest cząsteczka IF, przedstawiona na rys. 5.8. Ogólnie w grupie C_v, mamy operację tożsamościową £. (» — I) obrotów wokół pionowych osi symetrii oraz n odbić w pio nowych płaszczyznach symetrii przecinających się pod kątem 180 /n. czyli łącznic 2/t operacji.

Grupy punktowe C,_A oprócz wszystkich operacji symetrii charakterystycznych dla grup C'„ obejmują odbicie w poziomej płaszczyźnie symetrii <r_A. tj. płaszczyźnie prostopadłej do osi C„, oraz te wszystkie operacje, które wynikają z połączenia odbicia w płaszczyźnie z obrotami wokół osi symetrii. W grupie połączenie odbicia w płaszczyźnie a* z obrotem o ISO wokół osi Ci jest równoważne z przekształceniem w stosunku do środka symetrii, czyli z inwersją. W skład tej grupy wchodzą zatem następujące operacje symetrii: E. Ci. i oraz n, Przykładem cząsteczki o takiej symetrii jest płaska cząsteczka rr<rn.r-dichloroetylenu (rys. 5 9).

Do grupy C'_Jń obok operacji symetrii E. C,. C; oraz <r,. należą obroty wokół osi przemiennej Si (obrót o 120 wokół osi Cj i odbicie w płaszczyźnie os) oraz S< (pięciokrotny