356 2

3 56

8. Równania różniczkowe

5. Zagadnienie własne dla napiętej membrany kołowej jest następujące:

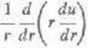
+Au=0,

gdzie u(l) = 0, a u'(0) i i/"(0) są skończone.

(a)    Zbudować równanie różnicowe dla siatki złożonej z punktów ^ = (2/- l)/(2#₊ l)

(/= — 1, 0_____ N). (Wobec tego zero leży między dwoma punktami siatki i A=2/(2W+1))

(b)    Wyznaczyć najmniejszą wartość własną, najpierw dla A^r=l, a potem dla N=2 Wykonać ekstrapolację Ricbardsona (zakładając, że błąd jest proporcjonalny do h¹)

(c)    Dla dużych N byłoby wygodnie korzystać ze standardowego programu obliczania wartości własnych macierzy symetrycznych. Jak wyrazić powyższe zagadnienie w odpowiedniej przy tym postaci?

Uwaga. Zero jest punktem osobliwym dla równania różniczkowego, ale nie dla jego rozwiązania. Ta osobliwość nie sprawia kłopotów w powyższych obliczeniach.

6. Pokazać, że równanie (8.4.4) jest liniowe, gdy równanie różniczkowe (8.4.1) jest liniowe - nawet wtedy, gdy jego współczynniki zależą od x. Pokazać też, że jeśli równanie różniczkowe jest liniowe, to wielocelowa metoda strzałów daje układ liniowy względem v(0>.

8.5. Równania różnicowe

W obliczeniach numerycznych ważną rolę odgrywają wzory rekurencyjne. Wzór re-kurencyjny

(8.5.1)    y»+\.....•»)

można też, zgodnie z twierdzeniem 7.1.2, napisać w postać-

(8.5.2)    Sy_m**ff(y.. Ay„...., A^k~V.. n).

Równanie typu (8.5.1) lub (8.5.2) nazywa się równaniem różnicowym rzędu k-tego. Jcg° rozwiązanie jest określone jednoznacznie, gdy jest danych k wartości początkowych y₀. >!»..•» J’*-i • Tc wartości można wybrać dowolnie — przynajmniej wtedy, gdy funkcj-/ jest wszędzie określona.

Przykład 8.5.1. Z równania różnicowego y*+_z-5>„₊₁ -r6y_a=0 z warunkanu P°" czątkowymi >’_o=0, ^ = 1 otrzymuje się kolejno

y₂=5 • 1 —6*0=5_:

y₃=5-5-6-l = l9, y₄ = 5 • 19—6- 5=65 itd.