c2 (5)

Rozdział 5
3. Wyznaczyć granice ciągów: a) lim [n2 + 2n - 1) = oo
n—> cc
ponieważ mamy sumę [oo+ oo] e) lim Jn2 + n = lim nil + = oo
Yl—>-CC Yl—>-CC
ponieważ oo razy liczba daje oo
I) lim 2n2~n+1 = 0
3»3+2
ponieważ stopień licznika jest silnie mniejszy od stopnia mianownika
r) lim iEEL =lim _lJEL = l
Yl—*-CC Yl—*-CC
ponieważ współczynniki przy najwyższych potęgach są sobie równe
v) lim
Yi—>yz
yi>-2yi+\
1+2m+9wj>
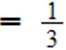
Wyszukiwarka
Podobne podstrony:
Zdjecie305 OWkz granice ciągów: lim n2-n + l 2-2 « 1 -4w4 — 5/7 + 7 > «3 + 4/72
6 (270) 09.04ANALIZA MATEMATYCZNA KOLOKWIUM I, grupa C Zadanie 1. Oblicz granice ciągów: a) lim •Vw3
c5 (2) Rozdział 5 a~” = a”5. Obliczyć granice ciągów: a) lim [(4)tt + 3-4-" + 2] -lim [(4)"
028(1) Wyznaczyć granice: 86. lim (
e trapez OBLICZANIE GRANIC CIĄGÓW r r lim n
152 (2) Zadania ZADANIA 1. Wyznaczyć granice: x2 + x — 6 a) lim x->2 x 2-4 g) lim :;4 - 8x3 + llx
DSC08025 Kolokwium z Analizy Matematycznej I gr.B, 10 stycznia 2008 1. (3p.) Wyznacz granice funkcji
IMG335 2 6. Obliczyć granice ciągów: 1 +4+7+...+(3n—2)•) " P l-2+3-4+„.—2n b) Vn2+1 c)
kolo 1. Oblicz granicę ciągów: f b) -1-
Granica funkcji zadania 5.6. Wyznaczyć granicę funkcji 1) lim (3*2 -5*+ 2), j-*2 3) lim (2*2+3*2-5
Dziawgo; Granice ciągów liczbowych 3 112 Granice ciągów liczbowych gdzie lim n—>=o 3n-2 3n-2 3n-2
dziawgo; Granice ciągów liczbowych 4 114 Granice cic{gów liczbowych t) limVl + 3” +5" +7” , 1 -
PB032251 i) fln — 2n:. "/]T21 + 2- 22 + ... + n • 2”, S — * n- n2 + 1 cos 2_1 2n — 1 Wyznaczyć
Image2021 2n + 5*fn m hm - n + 3 + co + co 2n + 5 Jn n lim • n2 +3 lim 2 r - + 5n n_■V 3 2 0+0T
Dziawgo; Granice ciągów liczbowych 2 110 Granice ciągów liczbowychg) lim£^lM n^°° 11 +1 3n+2 _ 5.4n+
więcej podobnych podstron