DSC02447 (2)

zm VI. Ctfb riaomcMi

ftmfcęt! pierwotnych funkcji / używamy eoft^ nieoznaczoną ftukgj

#3    JJfcH*,

m czytamy ,jah±f{x) po dzT. Pniikgę / nazywamy funkcją podcałkową, IX — zmienną edkemmw. Z podamy poprzednio określenia funkcji pierwotną wynika, te

Ę0Ę    j'/(*)d*«P(*)+C,

ffimt F jem hmmą pierwotną tuakąif, C — dowolną stalą, zwaną stałą całkowania, 2rnąmeemm całek funkcji/ nazywany całkowaniem funkcji f. Ponieważ obliczenie całki 4ąpt w yltfinrt od C rodzinę funkcji pierwotnych, stąd nazwa rozważanego rozdziału:

Mani; ani twierdzenie dotyczące istnienia całki.

Twnuinmr. 2. Kaida funkcja ciągła na przedziale X ma na tym przedziale funkcję pier-

Dowód panąmmy. Naloty dodać, te mogą istnieć ftwkcje pierwotne pewnych funkcji amoąftah

jodowanie fanhtyi pierwotnych, czyli całkowanie, jest znacznie trudniejsze od obli-om partu irtnyrh. ponieważ definicji całki nie podąjc sposobu jej obliczania. Poza

tym fwhy pierwotne widu funkii elementarnych, jak np. /(x) «■#“'* lob /(x)—_-

x

■e ^ ptf ftmkgami elementarnymi.

Zainwam ®ę istBtpretaqją geometryczną funkcji pierwotnej. Ponieważ f /(x)dv*»F(x) + ^C. więc funkcta FU i jest jedną z funkcji pierwotnych funkcji/(*), to znaczy

*»«/(*)

Zawalmy icwaucceśnie, te styczna do krzywej IM    y»f(zHC

m w pankrw 1*15 współczynnik kątowy IM#    tg«=[F(x)+C]^,,=*/(x<»).

Zatem pop reh nwaniii szukamy krzywych, dla których znamy w każdym punkcie współczynnik fapBoy ^uaą. Krzywe te nazywamy krzywymi całkowymi. Jeśli więc mamy kupią całkowi ?=FUi to przesuwając ją równolegle o wektor rfO, C] otrzymujemy inną kriywą talkową.' =    gdzie C jest stałą (ryt. 6.1). Mając dany punkt P(«, b) możemy

wyi—'iii wnośg męką C dte krzywej v*f\x) + C przechodzącej przez dany punkt F:

Ml

h*F(«)+C,

C«fe-F(a).

Pracz punkt F prapcfcoda iriy jedna krzyw* crikon o tówuia (6-8)    7-F^-FM.

Liczby aib nazywamy iwrsodrajmfpaczĄtkomymt,t nmet mhfwiy pracz nie aa krzywą całkową nazywamy warmkitm poaą&zmym.

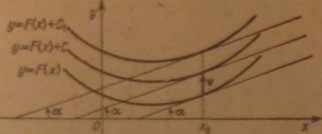
Ku. il

Wracając do okrefieak caflri nrnmTuoirj awilay, te aa podcawic wroni (il) i oznaczenia (i2) możemy napisać

■/W.

L[

<&J

(«)

^jj!~dx«F(jc)+C lab f r{x)ix=F{x)+C.

| dx

Ze znanych wzorów na pochodne funkcji i z określenia (6.1) wynikają następujące wzacy podstawowe:

JOdx«C,	J oos x dx =sin x+C,
f lćx*xfC«	f—r~ dx«Hx-fC, J corx
f i Z^141 ' '■ I JK*dx«—-+c (fc#-l), J Hi	f—j-dx o-ctg x-f C, J da x
	f-—dx=arctg.x+C= -arcctf x+C, J 1+JT
J tn«	^ 2 i —y—dx«iicaax+C* -uccoixłC,
f e*rfx-«S-C,	(sinhxdx =coshx+C\
f stnxdx~ —cosx + C,	| OCfish x dx * sinh x % C.

Równiei na podstawie znanych zasad rótoiczkowama można wypowiedzieć następujące twierdzenie: