DSC07077 (6)

86

Ciągłość funkcji

d*)przez dowolny punkt wewnętrzny wielokąta wypukłego można przeprowadzić sieczną w ten sposób, aby punkt ten był jej środkiem.

Rozwiązanie

Rozpoczniemy od przytoczenia twierdzenie Dorboux o przyjmowaniu wartości pośrednich: jeżeli funkcja / jest ciągła na przedziale [a,6j oraz spełnia warunek /(a) # /(6), to dla każdej wartości w położonej między /(o), /(6) istnieje punkt c € (a, 6) taki, że /(c)=w.

a) Niech x oznacza odległość pociągu od Szklarskiej Poręby. Ponadto niech T(x) oz-nocta opóźnienie (wyprzedzenie) pociągu w chwili, gdy był on w odległości x od stacji początkowej. Oczywiście funkcja T jest ciągła na przedziale [0,500], gdzie 500 (km] jest długością trasy. Z danych ^,ł|^^,na mamy

7(150) = —5 [min] dla Wrocławia, r(500) = 15 [min | dla Warszawy.

Zatem z twierdzenia Oarboux wynika, że T (zo) = 0, gdzie 150 < zo < 500. To oznacza, ze w pewnym miejscu między Wrocławiem i Warszawą pociąg był zgodnie z rozkładem judy.

I ■!■*/•!

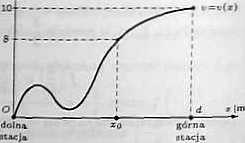
b)    Niech z oznacza odległość punktu wy dągn od dobrej stacji oraz niech c(z) oznacza prędkość wiatru w tym miejscu. Funkcja v jesz ciągła na przedziale [O.dj, gdzie d oz-nacza długość wyciągu (rysunek). Z danych zadania mamy warunki: o(0) = 0, tf(d) = 10 oraz «r(p) < 8 < trfd). Stecując twierdzenie Darbouz o przyjmowaniu wartości pośrednich do funkcji v na przedziale [0, dj i wartości ojj = 8 otrzymamy, że dla pewnego zo € (0,d) mamy v(zq) =8. Oznacza to, że w odfcgfcści zo od dolnej stacji wieje wiatr z pngUmścią 8m/a.

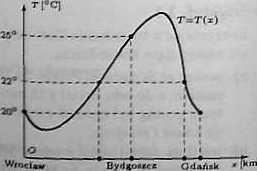
c)    Niech z oznacza odległość punktu trasy od Wrocławia oraz niech T(x) oznacza temperaturę panującą w tym miejscu (rysunek).

Funkcja T jest dągta na przedziale [0,450]

(odległość Wrocław - Gdańsk jest równa 450 km. a Wrocław - Bydgoszcz 270 km). Z danych zadania wynika, że T(0) = 20° C,

T(270) s 25° C, T(450) = 2tfC. Stosując twierdzenie Darbouz do funkcji T, wartości To = 22* C oraz przedziałów [0,270),

(2TO.45GJ wnioafcojeny. że we wnętrzu każdej z nich aą punkty, w których funkcja T payjuujc wartość 22* C. Oznacza to, że ■nędzy Wrocławiem i Bydgoszczą oraz mię-dzy Bydgpoczą i Gdańskiem będą miejsca, w których jest tempertura 22'' C.

Ili    PRej^du icmpctur. na trró nic zmie-

Zadania

87

niala się.

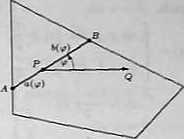
d*) Niech P będzie dowolnym punktem wewnętrznym wielokąta wypukłego. Ponadto niech PQ będzie ustaloną półprostą, względem której będziemy mierzyli kąt <p z sieczną AB (rysunek). Dla ustalonego kąta 0 $ y? $ ir niech a(^) i b{<p) oznaczają odpowiednio długości odcinków AP i PB cięciwy, tworzącej kąt z półprostą PQ. Rozważmy funkcję

IM = a(<p) - b(ip).

Funkcja ta jest ciągła na przedziale [0, łrj oraz spełnia warunki

/(O) = «(0) - 6(0),    /(w) = a(w) - 6(») = 6(0) - a(0) ~ - [o(0) - 6(0)].

Ponieważ funkcja / w punktach ip = 0 i <p = jt przyjmuje wartości różnych znaków, więc z twierdzenia Darboux wynika, że / (^o) = 0 dla pewnego 0 ^ po ^ *. Oznacza to, że punkt P jest środkiem cięciwy AB tworzącej kąt z półprostą PQ.

Zadania

• Zadanie 3.1

Korzystając z definicji Heinego uzasadnić ciągłość podanych funkcji na R : ^a) “(*) = _a3 _{+ 2}^;    b)    = sin² x;    c) w(x) = y/\x - 5|;

d) z(x) = 2“*;    e)    f(x) = 2x - 5;    f) g(x) = sin z;

g) A(z) = $x;    h)    p(x)    = e*;    h) t{x) = y/x* + lcosi.

Zadanie 3.2

Wyznaczyć zbiory punktów ciągłości podanych funkcji:

a) u{z)=[x* -x)E[x)\

c) _W(x) m

i

xcos — X

0

dla x < 0, dla x = 0,

v/xsin-^= dla x > 0;

v^x

e) 3(1) = E(x)(x -1);

g)p(i) = sgn(x^J)cos|i;

PL

b) u(x) = < xsmx [ x(x-jt)

dla x = 0 łub ir, dla x 5Ć 0 i jt;

d) z(x) =

1 al)=

/l — cos2z

sin

0

dla x ^ 0, dla ar= 0;

dla x = kx, k 6jZ, dla x jć fcr,' fc € Z; dla x < 0,

i

v/xcoa g dla x > 0.