DSC07082 (4)

Pochód

ne

funkcji

n Niech acl. Wtedy

p{xo +■ Axj —p{¹o'

—a® — A¹ —¹d —xi, lin, 5-Z£-- -<r lim

-A¹

e — 1

As

A¹—o -Az

l - -.“¹0

e» — 1

IT Miny tutaj s róumdri Hm _ -•—-o    ■

•ftijlfcif o

Napamć fówoanm stycznych do wykresów podanych funkcji we wskazanych punk-

B8S

a) /{¹) = (X + I) ¹5=7. c-l, /(-l»; b) /(i) = X¹. (2, /(2)).

Htmfipwis

■■Idmy a ni—»u stycturj do wykresu funkcji f = /(¹) w punkcie (-¹0. / (x₀)):

*-/(¹•)-/C²) (¹“¹»)•

?) Manty

/w=fx+ ij^s^n.so = -i, /(-u=o

wyrwirj mpamfc p-0 = W(f-(-|)),iml

f ¹ W(¹ +1).    1

ag

*•²• /(2) = 4 oraz /¹<¹) = [x¹ (In¹ -f- l)|.._a = 4(ln2 + I).

Bi—fe «ye=¹i » potać , - 4 = 4Qn 2 + I)(x - 2} .stad

® = 4ht(2e)(¹-2)+4._

m f(¹h

gdzie xo jest odciętą punktu przecięcia obu wykresów.

a) Znajdziemy najpierw punkt, w którym przecinają się wykresy funkcji y = e“. y = Mamy e¹ =    <=> i = 0.

Ponadto, mamy

= «³l—o =    |

Zatem

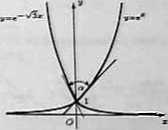
tg O =

l + >/5

l->/3

= 2+ >/§.

Stąd o = arctg(2 + v/5) =

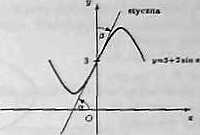
b) Korzystając z interpretacji geometrycznej pochodnej funkcji wnośmy, że styczna do wykresu funkcji /(x) = 3+2sinz w punkcie xo = 0 jest nachylona do osi Oz pod kątem

a = arctg [/ (xo)] = arc lg(2 cos 0)

•.?= arc tg 2.

Zatem kąt /3. pod którym wykres funkcji / przetnie od Oy, jest równy 0 = ^-arc tg 2 = arc tg-a: 0.46 [radj.

1

Przykład 44

2

Obliczy¹ kąt. pod którym:

a| przecinają aę wykresy fanfceji y = c¹. y ¹

b| wykres funkcji y = 3 + 2smx przecina oA Oy.

Ptmdąrmls

^T1łł®^pm kąta ostrego o. pod którym przecinają de wykresy funkcji y - /W^{1 1} jest ofcrafluoy mfrtmdrią

3

Przykład 4.5

a) Samolot podchodzący do lądowania porusza się po luku paraboli w cen sposób, że w miejscu lądowania trajektoria lotu jest styczna do płyty lotniska (rysunek). W jakiej odległości od wieży kontroli lotu wyląduje samolot, jeżeli w odległości O = 9 km znajdował się on na wysokości H = 400 m, a w odległość d = 6 km był na wysokości h = 100 m?

b³)Stół bilardowy ma kształt elipsy. Pokazać, że kula wypuszczona z ogniska elipsy po odbiciu sprężystym od brzegu bilardu przejdzie przez drugie ognisko.