DSC07124 (5)

176

Badania funkcji

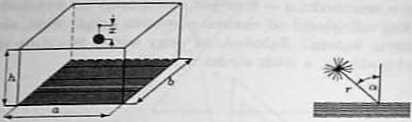
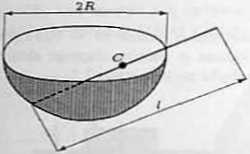
h*) Do kotła w kształcie półsfery o promieniu R włożono jednorodny pręt o długości l = 3R. Określić położenie równowagi pręta (nie uwzględniać tarcia pręta o kocioł).

Wskasówlst. Pręt będzie w położeniu równowagi, gdy jego środek muy C zajmie najniższe położenie.

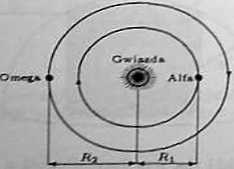
i) Odległy układ planetarny składa się z gwiazdy i dwóch planet. Planeta Alfa obiega gwiazdę w odległości Ri = 3 000 000 km w ciągu 11 = 3 lat ziemskich, a planeta Omega w odległości R? = 5000000 km w ciągu lj *4 lat. Obie planety poruszają się ze stałymi prędkościami w tym samym kierunku i w tej samej płaszczyźnie. Położenie planet 1 stycznia 2001 r. przedstawiono na rysunku. Kiedy będzie najdogodniejszy moment do obserwacji planety Alfa z planety Omega, tzn. kiedy odległość między planetami będzie najmniejsza?

J) Pewną substancję przechowuje się w kopcach w kształcie stożka. Jaki powinien być kąt nachylenia tworzącej stożka do podstawy, aby powierzchnia parowani* tej substancji (tj. powierzchnia boczna stożka) była najmniejsza?

7

Całki nieoznaczone

Przykłady

Całki nieoznaczone

• Przykład 7.1

Obliczyć podane całki nieoznaczone:

^a) J    b) J dx\    c) Jctg³ lir;

^d) J ^    <fc; e) J siir^ dĄ f) J \JxfZfŻdx.

Rozwiązanie

a) Korzystając z liniowości całki oraz zc wzoru

[_x°dx = 2-£r+C_t

J V'-'- 0 + 1

gdzie o jć -i, mamy

= |e^»-5y?₊c = |*^,^-|*ł^s+a

“) "'ykorzjrjtuJąc wzór

/“'•'* = EI^+0,

177 J