DSC07112 (5)

154

Badanie funkcji

b) L Dziedziną funkcji g{x) = ^ j«t przedział (O. co).

II. Fbnfcęja g jest ciągła w swojej dziedzinie, bo jest ilorazem funkcji ciągłych. Miejscem zerowym funkcji jest x = 1.

UL Obliczamy granice funkcji g na „krańcach” jej dziedziny. Mamy

tn x    —©o    ..    In x roo~l u i. 1    .

hm -=    ■ == —oo oraz lim -I — I = hm — == 0.

z-—0~ x O -    x—oo X | oo | X—eo X

I\'. Na podstawie wartości powyższych granic stwierdzamy, że prosta x = 0 jest asymp* cocą pionową prawostronną funkcji g. a prosta y = 0 jest asymptotą poziomą tej funkcji

V. Zbadamy teraz pierwszą pochodną funkcji g. Mamy D₉> = (0, oo) oraz

i, v 1 — lnx

g w = p •

Korzystając z warunku koniecznego szukamy punktów, w których funkcja g może mieć ekstrema- Mamy

1 — lnx

g\x) = 0

— 0

x = e.

Przy pomocy pochodnej ustalimy teraz przedziały monoton ięzności rozważanej funkcji Mamy

g'(x) > 0 <=> -—=-^ > 0 <=>l — lnx > 0 <=> 0 < x < e.

Funkcja g jest zatem rosnąca na przedziale (0, e). Podobnie,

g' (i) < 0 <=> x > e.

Funkcja g jest zatem malejąca na przedziale (e.oo). Z powyższych rozważań wynika, że hmkcja g ma w punkcie x = e maksimum lokalne właściwe równe e~^l.

VL Przechodzimy teraz do badania drugiej pochodnej. Mamy Dg>» — (0, oo) oraz

/// «

9 (*) =

21nx — 3

Z warunku koniecznego szukamy punktów, w których funkcja g może mieć punkty przegięcia. Mamy

ffW = 0

-k**.—— =0 <=> 2 In x — 3 = 0 <=> x == e^

Przy pomocy drugiej pochodnej ustalimy przedziały wypukłości rozważanej funkcji. Mamy

2lnx — 3 R    .    .    .v-.    4

-—j-> 0 <=> 21nx — 3 > 0 <=> x > e .

ITC|) > 0

Ftmkcja g jest zatem ściśle wypukła na przedziale f e* ,oo^. Ponadto

g'\x) < 0    0 < x < e V

Badana funkcja jmt zatem ściśle wklęsła na przedziale (o.e*). Z powyższych rozważań wynika, ze punkt ,|e jest punktem przegląda wykresu funkcji g.

pizytfwy    155

VII. Wyniki uzyskane w punktach I-VI zestawiamy w tabeli:

a    O 0<*<« • e a<«<ał    • •^<■<•0 j oo

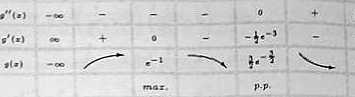
VIII. Na podstawie tabeli sporządzamy wykres funkcji g.

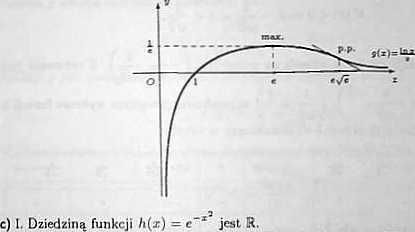
II.    Funkcja h jest parzysta i ciągła na R. Funkcja h nie ma miejsc zerowych i nie jest

okresowa.    ^Ą.,. 3

III.    Obliczamy granice funkcji h na „krańcach" jej dziedziny. Mamy lim e"^ł = e“°°=:

0. Z parzystości funkcji h wynika, że także lim c~^x = 0.

*“•“60

IV.    Z wartości powyższych granic wynika, że prosta y = 0 jest asymptotą poziomą tej funkcji w obu nieskończoności ach.

V.    Zbadamy teraz pierwszą pochodną funkcji h. Mamy D_h' - R oraz h'(x) = -2ze“ . Korzystając z warunku koniecznego szukamy punktów, w których funkcja h może mieć ekstrema. Mamy

h!(x) = 0 <==> - 2xe“*^ł = 0 <==> x = 0.

Przy pomocy pochodnej ustalimy teraz przedziały monotonicznóści funkcji h. Mamy h'(x) > 0 <=> — 2xe”*⁹ > 0 <=> x<0,

Funkcja h jest zatem rosnąca na przedziale (—c©,0). Z parzystości funkcji h wynika zatem, że jest ona malejąca na przedziale (0,oo). Z warunku wystarczającego wynika, że funkcja h ma w punkcie x = 0 maksimum lokalne właściwe równe 1.

VI.    Przechodzimy teraz do badania drugiąj pochodnej. Mamy Dh" = R oraz h'\x) = 2(2*³ - l) c~^x . Z warunku koniecznego szukamy punktów przegięcia wykresu funkcji fti Mamy

h!'(x) = Q<=> 4 |^f - || e“^ł* = 0<=>* = ~lubz = ™|