DSC07113 (5)

256    Badanie funkcji

Przy pomocy dn^iej pochodnej ustalimy przedziały wypukłości rozważanej funkcji. Mamy *'(*)> 0    <=>    4 (** -§) «"*’> o

~ (*~A)(^x+£)^>0

<=> x <--5= lub X >

y/S    Z2

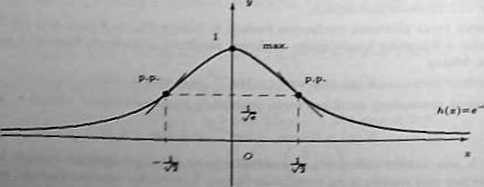
Fimkcjx h jest zatem ściśle wypukła na przedziałach    (i ,oo^. Ponadto

Żalem badana funkcja jest ściśle wklęsła na przedziale    . Z rozważań tych

wynika. że

VIL Wyniki uzyskane w punktach I-VI zestawiamy w tabeli

punkty -^=»e    ^-^,e są punktami przegięcia wykresu funkcji A-

d) * Dńedzma funkcji p(x) w    j«t zbiór (-oo.-l)u (-1.1) U (l.oo).

Łf^lata^ cięgla na swojej dziedzinie i ma miejsce zerowe tylko w punkcie x * °* ^OWiŁLUJi> *^r*^oioe    p na .krańcach" jej dziedziny. Mamy

-r

lim

*—i- I —

O*

C30S

Hm -■ ■ 3

*—40 1 — X*

O.

II f #• I					1 ^0
*"ut	•		•.		1 —	—	s	♦ I •
•'M	I a	*	v*.'ł		s	-	-v*-*	_ 119
HO	a		" .-ł		t * z- ■	~---X
			s-r-		■Uł.		pp-

Vm Na podstawie tabeli sporządzamy wykres funkcji.

Z nieparzystości funkcji k wynika, ic

T=** = «•=    .Jf,*    = a

IV.    Z poprzedniego punklu wynika zatem, że proste * =s — i_{f z} = l są asymptotami pionowymi obustronnymi tej funkcji oraz, że prosta y = 0 jest jej asymptotą poziomą w obu nieskończonośclnch.

V.    Zbadamy teraz pierwszą pochodną funkcji p. Mamy Dy = D_p oraz

** + l

^p(*^{) =} (T^ij5-

Funkcja p nic ma ekstremów lokalnych, bo

p'(*) *=    ^ 0, dla * € D_p

Funkcja p jest rosnąca na każdym z przedziałów dziedziny, bo dla x € Dy mamy

^pW = (f^^>a    _

VI.    Przechodzimy teraz do badania drugiej pochodnej. Mamy Dy = Dp oraz

P»

2x (x² + 3)

Z warunku koniecznego szukamy punktów przegięcia wykresu funkcji p. Mamy

,    2x (x^a +3)

p (*) = 0 <=>    » 0 <=> x » 0.

Pizy pomocy drugiej pochodnej ustalimy przedziały wypukłości rozważanej funkcji. Mamy

p"(x) > 0 <=> x < —1 lub 0 < x < 1.

Funkcja jest zatem ściśle wypukła nn przedziałach (-oo,-1), (0,1). Z nieparzystości tej funkcji wynika, żc jest. ona ściśle wklęsła na przedziałach (—1,0), (l.oo). Z rozważań tych wynika dniej, żc jedynie punkt (0,0) jest punktem przegięcia wykresu funkcji p. W punktach z = — 1, x = I funkcja wprawdzie zmienia rodzaj wypukłości, ale punkty te nie należą do dziedziny funkcji.

VIL Wyniki uzyskane w punktach I-VI zestawiamy w tabeli:

*	—oo	—oo < a < —1	i	-»♦ -1 < * < 0	0	o < * < i »-	1 < * < co	oo
£*•(*>	0	•f			0	**	-	0
p* (*)	0	ffc		+ H	> i	♦	■#*	0
J»(«)	0		oo	—oo *"	0 pp-	CO “*»		0

VIII. Na podstawia tabeli sporządzamy wykres funkcji.