DSC07119 (5)

168 Badanie funkcji

Rozwiązanie

£? u³

Kieda punkt 5(p.ę) należy do luku elipsy —- + Ł. = i leżącego w pierwszej ćwiartce układu (rysunek). Wtedy 0 < p < 2 oraz q = Z)jl - y- Równanie stycznej do elipsy

9	V B
	0	3 A *

w pnnkrir S(p,ę) ma postać

Styczna ta przędna oś Oz w punkcie A o współrzędnych ( —,0 ] i oś Oy w punkcie

li

Pole AOAB

B o współrzędnych wyraża się wzorem

18

Plp) = i\OA\\OB\ = - =

2    M p,

grfw 0 < p < 2. Ponieważ funkcja P przyjmuje tylko wartości dodatnie, więc jej wartość najmniejsza będzie realizowana w punkcie, w którym funkcja /(p) = p³ (4 - p²) , tj. ŁwW wyrażenia z mianownika funkcji P. przyjmie wartość największą. Szukamy zatem wsrtnśri największej funkcji / na przrdzialr (0.2). Podstawiając u = p³, otrzymamy funkcję kwadratową p(u) = u(4-u), gdzie 0 < u < 4. Funkcja kwadratowa p(u) = -u² + 4u pazyjmuje wartość największą na przedziale (0,4) w punkcie u = tio = —    = 2.

Stąd wynika, że funkcja P przyjmuje wartość najmniejszą w punkcie p = po = y/2. Punkt 5, dla którego A0A8 przyjmuje najmniejsze pale, ma współrzędne

Przykład 6.13

Miaoa Mi. Ma położone po przeciwnych stronach rzeki trzeba połączyć drogą z nrrarra prostopadłym do brzegów rzeki o prostoliniowych i równoległych brzegach (rysunek) W którym miejscu należy zbudować most, aby droga łącząca te miasta miała najmniejszą długość? Wielkośd znane: / = 21 km, aj = 2 km, o_a = 12 km.

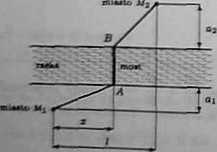
Rozwiązanie

Drap łącząca mineta Mi i Afj xna długość

d(x) * \MiA\ + \AB\ + |BAf_a|

« Vz^a+fl} + |AB] 4- Y/ji-zpł^,

gdzie 0 $ x < / Ponieważ odcinek AB (mott) ma stałą długość, więc wystarczy znaleźć wartość najmniejszą funkcji

/(*) = \A³ + o? + v/(£-*)>+o3

na przedziale |0./|. Korzystając z warunku koniecznego znajdziemy punkty, w których funkcja / może mieć ekstrema lokalne. Mamy

/(*)

2(f-»)•(-!) _ x

2_v/(Z-x)* + <4    y/*²*"

(I-*)

Stąd

/(*)

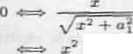
(/-X)

V(/-*)^a + a3 (l⁷ -2xl + x⁷ + a?) = (f² - 2xZ + x²) (x⁷ + a²)

0|f

(a? - a?) x³ + 2Za³x - /²a? = 0

<=> Z = ZO^B

Punkt aro =

Ol /

aa + «i

należy do przedziału (0,/|. Ponieważ pochodna f w punkcie aro

aj + a 2

zmienia wartości z ujemnych na dodatnie, więc funkcja J ma w tym punkcie minimum lokalne właściwe. Jest to jednocześnie punkt, w którym funkcja / przyjmuje wartość najmniejszą na przedziale |0, /]. Most należy wybudować w odległości xo = 3 km od miasta A/j (licząc wzdłuż brzegu rzeki).

i

się pod kątem prostym. Położenia	po-	♦	Pm -
czątkowe samochodów podano na	ry-		T *

• Przykład 6.14

Dwa samochody poruszają się ze stałymi szybkościami ni = 120 km/h, na = fiOkm/h po autostradach przecinających

rf_t

sunku: di = 50 km, d? ^s 20 km. Kiedy odległość między samo cho darni będzie najmniejsza?

Rozwiązanie

Niech Pi (£)t Pi(t) oznaczają odpowiednio położenia pierwszego i drugiego samochodu w chwili t. gdzie t ^ 0. Wtedy w układzie współrzędnych przyjętym na rysunku mamy P*(0 = (di - vi 1,0). Pi(t) = (0.d_a - t»aC) . Odległość między samochodami wyraża się wzorem

= \Z(f? + vl) t* - 2 (d,t., + «fa«a) t + (<ł? + A) dUl>a