DSC07118 (5)

166

Badanie funkcji

Stąd

W'(r) = 0«=»r=|/?

(pierwiastek r = —d odrzucamy, bo r nu być dodatnie). Zauważmy jeszcze, że

*V*(r) > 0 dla r > t/— oraz IV^#(r) < 0 dla 0 < r <

Oznacza to, żej funkcja IV jest rosnąca na przedziale | \/ — ,oo | oraz malejąca na prze-

o-i/- • Z rozważań tych wynika, że funkcja W osiąga w punkcie r_m|_B

mmnmnn lokalne właściwe i jest to jednocześnie punkt, w którym funkcja IV osiąga najmniejsza wartość na przedziale (0, oo). Wielkość Ania odpowiadająca wartości r^io równa

śę }j~' Przyjmując teraz V = 0.2 dm³ = 200000 mm³ otrzymamy

r«ałB = 10 {/— w 40 mm, Amin = 10 */— = 40 mm.

• Przykład 6.10

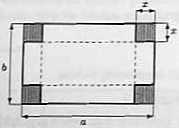
Jakiej wielkości kwadraty należy wyciąć na rogach prostokątnego arkusza kartonu o wymiarach o = 30 cm, b =

24 cm, aby pojemność pudełka otrzymanego po sklejeniu kartonu była największa?

Rozwiązarae

W rozwiązaniu przyjmujemy oznaczenia podane na rysunku. Niech V oznacza objętość pudełka otrzymanego po sklejeniu kartonu. Wtedy V(x) = (a — 2x)(6 — 2x)x, gdzie b < a oraz 0 < x < —. Z warunku koniecznego szukamy punktów, w których funkcja V może

mieć ekstrema (funkcja V ma pochodne dowolnego rzędu na przedziale 0 < z < Mamy

V^(x) = (-lic³ - 2^(0 + b) + abzY = 12z* - 4*(o + b) + ab.

Stąd

V\z)_BQ *=* nz¹ -Ax{a + b) + ab=0

(o + b) — yja* + b? —ab , , (a + 6) +    + ó³ — ab

^    *1 =S ---- luo ZJ S ----.

o    6

PiuhMKk sra odrzucamy, bo nie należy do przedziału ^0, Zauważmy jeszcze, ic > 0 dla 0 < x<x\ onz V^ł(x) < 0 dla z_x < z <

Przykłady

167

Oznacza to. że funkcja V jest rosnąca na przedziale (0,xi) oraz malejąca na przedziale Z rozważań tych wynika, że funkcja V osiąga w punkcie z = zj maksimum lokalne właściwe i jest to jednocześnie punkt, w którym funkcja V przyjmuje największą wartość na przedziale ^0, - j. Przyjmując o = 30 cm oraz 6 = 24 cm otrzymamy x—... = 9- v/5Ta*4.4 cm.

• Przykład 6.11

W kulę o promieniu R wpisano walec o największej objętości. Znaleźć wymiary tego walca.

Rozwiązanie

Niech r oznacza promień walca wpisanego w kulę, a z jego wysokość (rysunek).

Wtedy r* = /?*-(|) . gdzie 0 < x < 2/?.

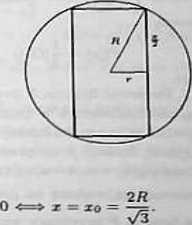
Objętość walca wpisanego w kulę wyraża się wzorem

V(x) = *r*x = ^ (4/1* - x²) x.

gdzie 0 < x < 2/7. Korzystając z warunku koniecznego znajdziemy punkty, w których funkcja V może mieć ekstrema. Mamy

"(*) = | (4«^a - 3x^a) .

S4d

V(») = 0 «=» 4R^ł - 3*^J = 0 <=> x = io =

/3

Z postaci pochodnej widać, że funkcja V jmł rrMnąra n» pnredzial^ (°.2*) im-kj*. na przedziale ^-^,2/7^ . Oznacza to, że funkcja ta przyjmuje w punkcie xo maksimum

47t|

3y/3

^ na przedziale (0,2/?). Promień walca o największej objętości wynosi r».. = */^/?, ą

75*

lokalne właściwe równe    = - ⁿ R* i jest to jednocześnie wartość największa funkcji

wysokość x,

• Przykład 6.12

u²

W którym punkcie elipsy ~ + — = l należy poprowadzić styczną, aby pole

trójkąta ograniczonego tą styczną i dodatnimi półoaiami układu współrzędnych było najmniejsze?