DSCF2519

$ 4,i, PtawdifpodiAfcństwo warttrfkowe

ą. ftafegie I pewne    prawóopodOłńeń^t wa

k

P(B)>0,

gdzie

|- 4.5. Prawdopo4ofc»*f»ł«r0 nznmknwe. Zdarz* się, te informacja o zajściu ŻdatZenią ff ma pewien wpływ na imrtćM obliczanego prawdopodobieństwa zdarzenia A,

Puzwład 4,5A. Rzucamy dwiema kostkami. Obliczyć prawdopodobieństwo:

j. zdarzenia A polegającego na otrzymaniu sumy oczek nie większej od czterech:

2.    zdarzenia & polegającego na otrzymaniu dwóch oczek co najmniej na jedtr, kostce'

3.    zdarzenia polegającego na tym, te co najmniej na jednej z ktrsiek otrzymamy d oczka i że suma oczek będzie nie większa od czterech;

4.    zdarzenia polegającego na tym₁ te suma oczek otrzymanych na obu kostkach będzie nie większa od czterech, jcMi wiadomo, te co na jmniej na jednej kostce otfZjmaru> dwa oczka,

Rozwiązanie,

}> Zbiór podstawowy J zdarzeń elementarnych przy rzucie dwiema kostkami je-.* następującym

|1 21 31 41 51 61

12    22 32 42 52 62

13    23 33 43 53 63

14    24 34 44 54 64

15    25 35 45 55 65

16    26 36 46 56 66,

Korzystając z klasycznej definicji prawdopodobieństwa (def, 4AA), otrzymujemy

P{A)»^\,

2,    Kfyrzystając, tak jak poprzednio, z definicji 4AA, mamy

W-ll

3,    Zdarzenie, którego prawdopodobieństwo chcemy obliczyć, polega na łącznym zajściu zdarzeń A oraz, % Otrzymujemy więc

4,    W rozwalanym przypadku zbiorem podstawowym jest zbiór tych par liczb -zdarzeń elementarnych zbioru /,, które zawierają co najmniej jedną dwójkę, Mamy jede-nafcie takich par, które zaznaczono przez podkręcenie, sprzyjające są tc pary liczb, których suma jest nic większa od czterech, % trzy takie pary, Szukane prawdopodobieństwo jest więc równe fyy

/darzenie ptAeg&jąfie na zajściu zdarzenia A, przy zaU/zeniu, że zdarzenie B zaszło, oznaczamy symbokrri A\B₍ a prawdopodobieństwo tego 'Zdarzenia P(A\B) nazywamy pruwdopoMUzhsIwem warunkowym, '/darzenie h jest tutaj zbiorem podstawowym zda-zdarzenia A\H,

Po wprowadzeniu powyższych oznaczeń możemy powiedzieć, te w ptsnkae czwartym przykładu 4.5.1 obtoczyliśmy prawdopodobieństwo warunkowe zdarzenia A przy warunku, te zaszło zdarzenie B, co zapiszemy', P(A\B)^y_f.

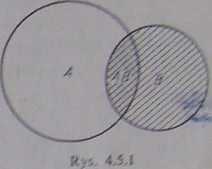
Pk/,yKf,Ai> 4,5,2, Niech n będzie fkrznofcią podstaw wowego Zbioru zdarzeń elementarnych, wir ód których jest k zdarzeń sprzyjających zajściu zdarzenia B_f a l zdarzeń sprzyjających zajściu zdarzenia AB (rys, 4AA),

Wtedy

l    11

P(AH)»e ,

oraz

P(A\By

bowiem podstawowy zbiór zdarzeń dla zdarzenia A B ma k zdarzeń elementarnych. Stąd

lik P(AB)

P(B)

Wzór na prawdopodobieństwo warunkowe, który uzyskaliśmy w przykładzie 4,5,2 przyjmując, te zbiór podstawowy zdarzeń elementarnych jest skończony, uogólniamy na dowolny zbiór zdarzeń elementarnych / na mocy następującego określenia:

OfcWWCM 4,5A, Prawdopodobieństwem warunkowym P(A\B) zdarzenia A przy założeniu, te zaszło zdarzenie B nazywamy iloraz prawdopodobieństwa łącz.nego zajścia zdarzeń A i B i prawdopodobieństwa zdarzenia B

Pi AB) P(B) *

Równość (4,5,1) można zapisać w postaci wzoru

(4.5.2)    P(A'B)mp(B)P(A\B),

który czytamy\ prawdopodobieństwo łącznego zajścia zdarzeń A i B jest równe iloczynowi prawdopodobieństwa zdarzenia B przez prawdopodobieństwa warunkowe zdarzenia A, przy założeniu, te zaszło zdarzenie B.

Wzór (4,5,2) można uogólnić na większą liczbę zdarzeń:

(4.5.3)    P(A_X' A_t-Ay...-Aj»

~P(At)'P(A₂\A_l)'F(A}ⁱ\AtA₂)'„.'P(A₀\A_tA₂...A_m„_l), bowiem posługując się kolejno wzorem (4.5.2) mamy P(A_iA₁...A_H)»P(AAP(A_tA_i...A_n\AA*‘

'■* P (A \ ) P (A i \ A i) P (A $ A ą ... A_ąj A f A 2)^... » ~f’lA_l)P{A_t\A_l)PlA,\A,A₁)...P(A,\A_lA₁.. A..,).