103972

Algebra liniowa z geometrią analityczną Lista 4: Liczby zespolone (cz. 1)

1. Wykonać działania (wynik przedstawić w postaci algebraicznej):

a) (3 - 2t)« + (1 - 3«)(2 + *), ^b) M " ² + 3*', c) i²³ + i⁵³³ - 2|-⁵⁷ +

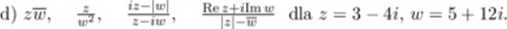
2. Znaleźć liczby rzeczywiste x. y sj>elniające równania:

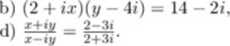
a) x(2 + 3«) + j/(4 - i) = -2 + 1 li,

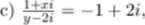
3.    W liczbach zespolonych rozwiązać równania:

a)*²+3s = 0, b)f±J = -l, c)z+ź+i(z-z) = -6+2i, d) (l+3i)z+4(z-2i) = l-9i

4.    Niech u =    t? =    Na jaszczyźnie zespolonej narysować zbiór wszystkich liczb

zespolonych 5, dla których:

a)    liczba u jest rzeczywista,

b)    liczba v jest rzeczywista,

c)    liczba u jest czysto urojona.

d)    liczba v jest czysto urojona.

5.    Na płaszczyźnie zespolonej narysować zbiory:

a)    A = {z € C : lin [(1 + 2i)z - 2 + i] > 0},

b)    Z?    = {z    € C    : Re(j + 2i)² < 0},

c)    C    = {z    € C    : 2 + i = z + 1},

d)    D = { 5    G C : |z + 3 — 5i| = 2}.

e)    E = {z    G C : 1 < \z + 2 — i| < 3    i    — 4 <    Im (iz)    < -1},

f)    F = {z    e C : |(2 - i)z - 5 + lOij    <    10},

g)    G = {z    e C : \z - 2 + 3*| > \z +    1 - i|},

h)    H = {z    € C : 2 < \z - 2 + tj < 5    i    \z +3*| <    \z - 4    - i|}

6.    Znaleźć najmniejszą i największą wartość modułu liczb należących do zbioru:

a)    A    = {z    e C    : \z + 4 - 3*| < 3},

b)    B    = \z    € C    : \z — 1 +i| = \z — 3    —1| i Re 5 > 0}.

7.    Zapisać w postaci algebraicznej elementy zbiorów:

a) v^-16 + 30i, b) y/=\8, c) >fi, d) v^8t, e) y/l + 2>/6i.

8.    W liczbach zespolonych rozwiązać równania:

a)    2² + (-3 + i)z + 8 + i = 0,

b)    10s² + 62 + 9 = 0,

c)    (2 - i)2² - (2 + 9i)2 - 9 + 7i = 0.

d)    2* + 132² + 36 = 0,

e)    z⁴ + (15 + 7i)2² + 8 - 15i = 0.