103974

Algebra liniowa z geometrią analityczną Lista 6: Wielomiany rzeczywiste i zespolone

1.    Obliczyć sumę i iloczyn wielomianów W i V oraz iloraz i resztę z dzielenia wielomianu W przez wielomian V, jeżeli:

a)    W(x) = 2x⁴ - 3x³ - 6* + 3, V(x) = 2x² - x + 2;

b)    W (z) = z* + (1 - i)z³ + 2iz²    + 2z    + 1 - 2*.    V{z)    = iz³    - 2:

c)    IF(z) = (z - 2i)⁵, V(z) = (z    + 3i)³.

2.    Znaleźć wszystkie pierwiastki całkowite wielomianu:

a) x³ -f x² - 4x - 4:    b)    3x³ - 7x²    + 4x - 4:

c) x⁵ - 2x⁴ - 4x³ + 4x² - 5x + 6:    d)    x⁴ +    3x³ - x² 4-    17x + 99.

3.    Znaleźć wszystkie pierwiastki wymierne wielomianu:

a) 4x³ + x — 1;    b) 4x⁴ 4- 4x³ 4- 3x² — x — 1;

C) X³ - gX² - §X - g;    d) X⁵ + jX³ - X² + gX - g.

4.    Znając jeden pierwiastek wielomianu W, znaleźć wszystkie pierwiastki zespolone tego wielomianu:

a)    W(x) = 2x³ - 12x² - 2x 4- 60, x\ — 5;

b)    W{x) = x³ — 3\/2x² 4- 7x — 3\/2, x\ = \/2 4- *;

c)    W(x) = x⁴ - 2x³ 4- 7x² 4- 6x — 30, xj = 1 - 3*.

5.    Podać przykład takiego wielomianu rzeczywistego możliwie najniższego stopnia, że:

a)    liczby 2, -3, y/3 oraz 1 - 2i są pierwiastkami jwjcdynczymi tego wielomianu:

b)    liczba 1 — i jest pierwiastkiem pojedynczym, liczby — 2i oraz 4 są pierwiastkami podwójnymi, a liczba -1 4- 2i jest pierwiastkiem potrójnym tego wielomianu.

6.    Wielomian zespolony W(z) przedstawić w postaci iloczynu dwumianów’, jeżeli:

a) W (z) = iz² + 2z - lOi:    b) W (z) = 2z⁴ 4- 10z² 4- 12:    c) W (z) = z³ - 6z - 9.

7.    Wielomian rzeczywisty W(x) przedstawić w postaci iloczynu nierozkładalnych wielomianów’ rzeczywistych, jeżeli:

a) łl'(x) = x⁶ + 8;    b) W(x) — x⁴ 4- 4;    c) W(x) — x⁴ — x² 4- 1;

d) W(x) = 4x⁵ - 4x⁴ - 13x³ 4- 13x² 4- 9x - 9.

8. Funkcję wymierną przedstawić w postaci sumy wielomianu i funkcji wymiernej właściwej:

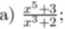
x⁴+2x³+3x²+-lx+5 x³+2xⁱ+3x+4’

9. Zaproponować rozkład zespolonej funkcji wymiernej właściwej na zespolone ułamki proste (nie obliczać nieznanych współczynników):

a)

b)

c)

iz+7

10. Zaproponować rozkład rzeczywistej funkcji wymiernej właściwej na rzeczywiste ułamki proste (nie obliczać nieznanych współczynników):

x²4-2x-7    u\    j³—Sr~ 1    _x⁴+x³_

x³(x—l)(x+5)² ’    (x²-H)(x²+x+3)³’    (x+3)²(x²-4x+5)²*

11. Zespoloną funkcję wymierną właściw^rą rozłożyć na zespolone ułamki proste:

^a) (*-i)(**+2)(*+3)^{:    b})    ^d) <P+&+V'

12. Rzeczywistą funkcję wymierną właściwą rozłożyć na rzeczywiste ułamki proste:

_\    12    i,\ x² .    _\    4x    j\ x²+2x    1 r\ x²+l

(x— l)(x—2)(x—3)(x—*l)’    *)    ^C) <x4-l )(**+!)»’ TP+ŚW* ^ P+x’ ^ł) x5(x+lP*