82369

Część 1    5. TEMPERATURA, OSIADANIA PODÓRI BŁĘDY MONTAŻU W RÓWNANIU... 24

W kratownicy tej sztywność pręt ów £4 jest stała, nie występują także siły tnące i momenty zginające w prętach (wynika to z definicji kratownicy). Pręty pasa górnego oznaczono literą G, pasa dolnego - D. kizyźulce - K oraz słupki jako S. Spójrzmy, jak będzie wyglądało ogólne równanie pracy wirtualnej dla prętów powyższej kratownicy:

RA

Wynika z tego. że obliczenie przemieszczenia punktu sprowadza się do pomnożenia siły od obciążenia wirtualnego w danym pręcie przez siłę panującą w tym pręcie wywołaną obciążeniem rzeczywistym i długości tego pręta. Następnie sumujemy wszystkie iloczyny i dzielimy wynik pizez sztywność EA. Otrzymana wielkość jest rzeczywistym przemieszczeniem danego punktu.

Licząc siły w prętach, będziemy zakładali rozciąganie (wynik ze znakiem minus oznacza więc ściskarue w pręcie). Wyznaczmy siły powstałe na skutek działania obciążeiua zewnętrznegoP:

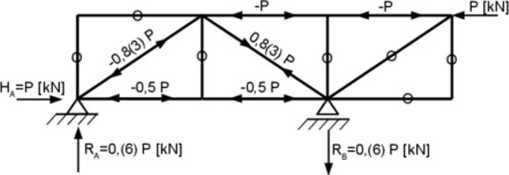
Obliczmy reakcje podporowe:

T.Y:R_a-R,

1 a Rb 6 0 -P 4,0=0 R„=R_A=0,6 |kN\

Wyznaczmy siły w poszczególnych prętach:

• Siły w piętach Si. S:. Sj. Si. D<. Ks. Gi - będą zerowa (wynika to z równowagi więzów).

• Siły w* prętach G; i G> będą równe co do wartości sile P i będą to siły ściskające. Obliczmy teraz siły w pi ętach Ki i K_:.

Y.Y Kj sin(x=- K_: sina

R_a+ K, sincx=0 K,= -0,83(3)P K_:=0,S3(3)P

AlmaMater

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.