ESTYMACJA

Def. Estymacją nazywamy szacowanie wartości parametrów, ewentualnie postaci rozkładu w populacji generalnej, na podstawie obserwacji uzyskanych w próbie losowej.

Typy estymacji:

- estymacja parameryczna

estymacja nieparametryczna

- estymacja punktowa

estymacja przedziałowa

ESTYMATORY

Założenia - rozkład zmiennej losowej X w populacji generalnej jest opisany za pomocą dystrybuanty
, gdzie jest parametrem rozkładu, od którego zależy ta dystrybuanta,

- nieznaną wartość parametru szacujemy na podstawie n-elementowej próby losowej

Def. Estymatorem
parametru rozkładu populacji generalnej nazywamy statystykę z próby
, która służy do oszacowania wartości tego parametru.

Def. Oceną parametru nazywamy konkretną wartość liczbową
jaką przyjmuje estymator
parametru dla realizacji próby
.

Def. Błędem szacunku (estymacji) parametru nazywamy różnicę pomiędzy estymatorem a wartością parametru, oznaczoną przez:

a za miarę tego błędu przyjmujemy wyrażenie:

Def. Średnim (standardowym) błędem szacunku paramertu jest wyrażenie

Def. Względnym błędem szacunku parametru jest wyrażenie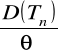

Poprawka dla błędów standardowych szacunku w przypadku losowania ze skończonej populacji:

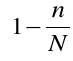
WŁASNOŚCI ESTYMATORÓW

Def. Mówimy, że estymator
parametru jest nieobciążony, jeśli spełniona jest relacja:

W przeciwnym przypadku estymator
nazywamy obciążonym, a wyrażenie:

nazywamy obciążeniem estymatora.

Przykład

- badamy populację generalną o dowolnym rozkładzie z wartością oczekiwaną

- średnia arytmetyczna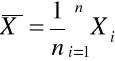
z n-elementowej próby losowej
jest nieobciążonym estymatorem wartości oczekiwanej w rozkładzie populacji generalnej gdyż:

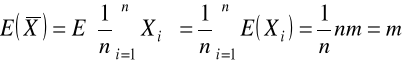
Def. Mówimy, że estymator
parametru jest asymptotycznie nieobciążony, jeśli:

Def. Mówimy, że estymator
parametru jest zgodny, jeśli spełnia relację:

dla dowolnego 0

Przykład

Twierdzenie (prawo wielkich liczb Czebyszewa)

Jeśli dla ciągu zmiennych losowych
, z których każda ma skończoną wartość oczekiwaną
oraz wariancję
, jest spełniony warunek:

,

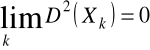
to

to znaczy ciąg
jest stochastycznie zbieżny do wartości oczekiwanej

Wniosek

Ciąg zmiennych losowych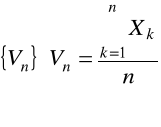
jest stochastycznie zbieżny do wspólnej dla wszystkich zmiennych
wartości oczekiwanej
, tzn.:

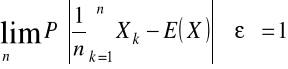
Średnia arytmetyczna z próby
jest zgodnym estymatorem wartości
w populacji generalnej, tzn.:

; >0

ZWIĄZKI POMIĘDZY WŁASNOŚCIAMI NIEOBCIĄŻONOŚCI

ORAZ ZGODNOŚCI ESTYMATORA

1. Jeśli estymator
parametru jest zgodny, to jest asymptotycznie nieobciążony. Twierdzenie odwrotne nie jest prawdziwe.

2. Jeśli estymator
parametru jest nieobciążony (lub asymptotycznie nieobciążony) oraz jeśli jego wariancja spełnia relację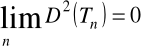
, to
jest estymatorem zgodnym.

Def. Jeśli dany jest zbiór wszystkich nieobciążonych estymatorów
parametru , to estymator
, który ma w tym zbiorze najmniejszą wariancję, tzn.
, i=1,...,r, nazywamy najefektywniejszym estymatorem parametru

Wyrażenie:

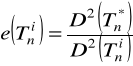
nazywamy efektywnością estymatora
parametru .

Przykład

Bierzemy pod uwagę dwa estymatory nieobciążone wartości oczekiwanej
w populacji generalnej o dowolnym rozkładzie:

• średnia arytmetyczna
  ,

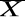
• - zmienna
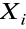
  charakteryzująca próbę.

Wiemy, że wariancje tych estymatorów odpowiednio wynoszą:

-

-

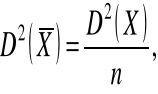
Ponieważ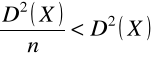
średnia arytmetyczna
jest efektywniejszym estymatorem wartości oczekiwanej
niż i-ta zmienna
z próby.

WYZNACZANIE WARIANCJI ESTYMATORA

NAJEFEKTYWNIEJSZEGO

Twierdzenie (nierówność Rao-Cramera)

Przy pewnych ogólnych warunkach wariancja
dowolnego nieobciążonego estymatora parametru spełnia relację:

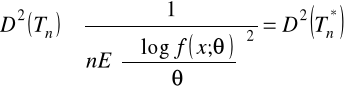
gdzie:

oznacza funkcję gęstości lub funkcję prawdopodobieństwa rozkładu populacji generalnej.

Def. Mówimy, że estymator
parametru jest asymptotycznie najefektywniejszy, jeśli:

PRZEDZIAŁ UFNOŚCI

Założenia

- cecha X ma w populacji generalnej rozkład z nieznanym parametrem ,

- na podstawie próby losowej
pochodzącej z populacji wyznaczamy takie dwie funkcje
i
, że dla każdej realizacji próby
jest
i dla, z góry przyjętego, prawdopodobieństwa 1- zachodzi:

Def. Przedziałem ufności parametru nazywamy losowy przedział
. Współczynnikiem ufności 1- nazywamy z góry ustalone prawdopodobieństwo, z jakim ten przedział pokrywa nieznaną wartość parametru .

(1)

(2)

(3)

(4)

(5)

m

PRZEDZIAŁ UFNOŚCI DLA ŚREDNIEJ m

W POPULACJI NORMALNEJ

ZE ZNANYM ODCHYLENIEM STANDARDOWYM

Założenia

- zmienna X ma w populacji rozkład
, gdzie średnia m jest nieznana, natomiast odchylenie standardowe jest znane,

- opierając się na próbie losowej
pobranej z populacji szukamy przedziału ufności dla m przyjmując współczynnik ufności 1-

Etapy

• szukamy estymatora parametru m

estymatorem jest średnia arytmetyczna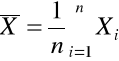
mająca rozkład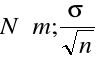

- standaryzujemy zmienną
uzyskując:

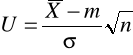
; gdzie: U

- definiujemy wartość
jako wartość w standardowym rozkładzie normalnym, dla której spełniony jest warunek

co zapisujemy:

- podstawiamy w miejsce U wyrażenie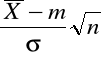

otrzymując:

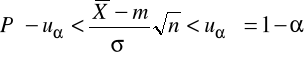
- przekształcając uzyskujemy przedział ufności dla średniej m o postaci:

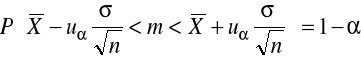
PRZEDZIAŁ UFNOŚCI DLA ŚREDNIEJ m

W POPULACJI NORMALNEJ

Z NIEZNANYM ODCHYLENIEM STANDARDOWYM

Założenia

- zmienna X ma w populacji rozkład
, gdzie średnia m oraz odchylenie standardowe są nieznane,

- opierając się na małej
próbie losowej
pobranej z populacji szukamy przedziału ufności dla m przyjmując współczynnik ufności 1-

Etapy

-szukamy estymatora parametru m

estymatorem jest średnia arytmrtyczna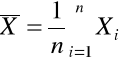
, którego rozkład nie może być wyznaczony ze względu na nieznajomość

- dla rozkładu t-Studenta o n-1 stopniach swobody i przy ustalonym definiujemy wartość
, dla której spełniona jest równość:

- podstawiamy w miejsce t wyrażenie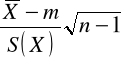

(gdzie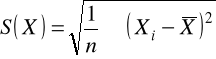
oznacza odchylenie standardowe z próby) otrzymując:

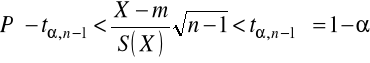
- przekształcając uzyskujemy przedział ufności dla średniej m o postaci:

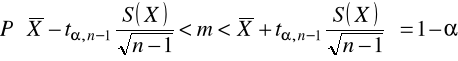
- opierając się na dużej
losowej
pobranej z populacji generalnej szukamy przedziału ufności dla m przyjmując współczynnik ufności 1-

Przedział ufności dla m ma postać:

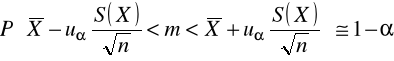
PRZEDZIAŁ UFNOŚCI DLA WARIANCJI

W POPULACJI NORMALNEJ

Założenia

- zmienna X ma w popualacji rozkład
, gdzie parametry m i są nieznane,

- opierając się na próbie losowej
pobranej z populacji szukamy przedziału ufności dla
przyjmując współczynnik ufności 1-

Etapy

- szukamy estymatora parametru

estymatorem jest wariancja z próby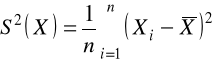

- dla rozkładu
o n-1 stopniach swobody definiujemy dwie wartości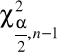
i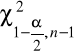
spełniające odpowiednio równości:

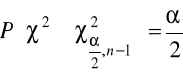
oraz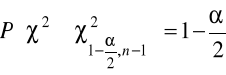

z których wynika, że:

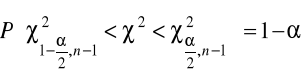
- podstawiamy w miejsce
wyrażenie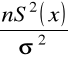
, otrzymujemy:

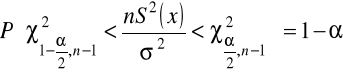
- przekształcając uzyskujemy przedział ufności dla wariancji
o postaci: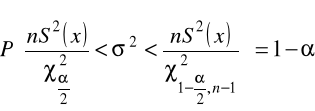

PRZEDZIAŁ UFNOŚCI DLA PARAMETRU p

W ROZKŁADZIE DWUMIANOWYM

Założenia

- zmienna losowa X ma rozkład dwumianowy z nieznanym parametrem p

- opierając się na dużej
próbie losowej
pobranej populacji szukamy przedziału ufności dla p przyjmując współczynnik ufności 1-

Etapy

- szukamy estymatora parametru p

estymatorem jest częstość sukcesów obserwowana w

n-elementowej próbie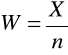
posiadająca asymptotyczny rozkład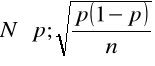

- standaryzujemy zmienną W uzyskując:

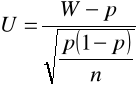
, gdzie U

- definiujemy wartość
jako wartość w standardowym rozkładzie normalnym, dla której spełniony jest warunek
co zapisujemy:

- podstawiamy w miejscu U wyrażenie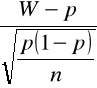
otrzymując

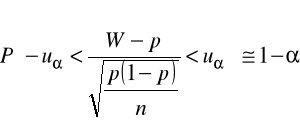
- przekształcamy nierówności w nawiasie oraz podstawiamy

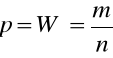
uzyskując przedział ufności dla p o postaci:

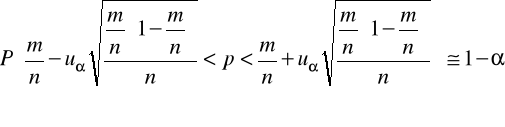
DOKŁADNOŚĆ ESTYMACJI

• bezwzględny (maksymalny) błąd estymacji (połowa przedziału ufności)

gdzie:

i
są odpowiednio górną i dolną granicą przedziału ufności

• względny błąd estymacji

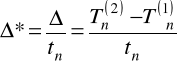
MINIMALNA LICZEBNOŚĆ PRÓBY

Estymacja średniej m w populacji normalnej ze znanym odchyleniem standardowym

• postać podziału ufności:

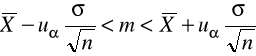
• długość przedziału ufności:

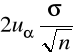
• minimalna liczebność próby zapewniająca, przy danym 1-α, nie przekroczenie przez bezwzględny (maksymalny) błąd szacunku z góry założonej wielkości d:

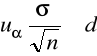
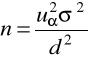
Estymacja parametru p w rozkładzie dwumianowym

• postać przedziału ufności:

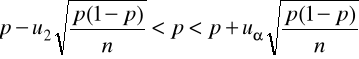
• długość przedziału ufności:

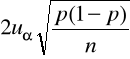
• minimalna liczebność próby zapewniająca, przy danym 1-α, nie przekroczenie przez względny (maksymalny) błąd szacunku z góry założonej wielkości d:

---