1

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Modelowanie i symulacja

dr inż. Piotr Piela

Zakład Metod Matematycznych

kontakt: pokój 28 

ppiela@wi.ps.pl

2

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – sposoby opisu

Nieliniowe systemy dynamiczne:

opis 

zależności 

wejście-wyjście 

za 

pomocą 

równań 

różniczkowych,

opis za pomocą równań stanu.

Liniowe systemy dynamiczne:

opis  zależności  „wejście-wyjście”  za  pomocą  równań 
różniczkowych,

opis za pomocą równań stanu,

opis zależności „wejście-wyjście” w formie operatorowej

3

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Rachunek operatorowy

Operatory

 odwzorowują  wielkości  wejściowe,  będące  funkcjami  np. 

czasu – w inne funkcje czasu – reprezentujące wielkości wyjściowe. 
Posługiwanie  się  operatorami  ułatwia  obliczenia,  gdyż  pozwala 
operacje na funkcjach zastąpić operacjami na liczbach.

4

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

Przekształcenie  Laplace'a

 jest  operatorem  przekształcającym 

funkcję  zmiennej  rzeczywistej  f(t)  na  pewną  funkcję  F(s)  zmiennej 

zespolonej s = c + j

ω

  zgodnie ze wzorem:

L

[ f t]=F s=

∫

0

∞

x

t⋅e

−st

dt

Odwrotne  przekształcenie  Laplace'a

 –  znając  transformatę 

funkcji   F(s)  możemy  wyznaczyć  samą  funkcję    f(t)  za  pomocą 
wzoru:

f

t =L

−1

[ F s]=

1

2

 j

∫

c

− j ∞

c

 j ∞

F

s⋅e

st

ds ,

t0 ,

c = Re s

5

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

L

[ f t ]=F s=

∫

0

∞

f

t ⋅e

−st

dt

F(s) – obraz Laplace'a funkcji f(t),
f(t) – oryginał – funkcja spełniająca następujące warunki:

●

funkcja f(t) jest ciągła dla wszystkich wartości t,

●

 funkcja f(t) musi spełniać warunek

●

wartości funkcji f(t) muszą być  ograniczone,  zawsze można 

określić dwie liczby M > 0 i 

α

 ≥ 0, że spełniona jest równość: 

f

t =0 ;∀ t0

f

t Me

 t

;

∀ t0

6

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

Właściwości transformaty Laplace'a:

addytywność i liniowość - przekształcenie Laplace'a spełnia 

zasadę superpozycji,

L

[af

1

tb f

2

t ]=aL[ f

1

t ]bL[ f

2

t]=aF

1

sbF

2

s

skalowanie (a – liczba rzeczywista, dodatnia),

L

[ f at ]=

1

a

F



s

a



F

as=

1
a

L

[

f



t

a



]

tłumienie oryginału (b – dowolna liczba zespolona),

L

[

e

−bt

f

t

]

=F sb

7

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

przesunięcie w prawo o a (a – liczba rzeczywista, dodatnia),

L

[ f t−a]=e

−as

F

s

przesunięcie w lewo o a (a – liczba rzeczywista, dodatnia),

L

[ f ta]=e

as

[

F

s−

∫

0

a

f

t ⋅e

−st

dt

]

8

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

różniczkowanie oryginału,

L

[ f ' t]=sF s− f 0 ,

f

0= lim

t

0

f

t 

L

[ f ' ' t ]=s

2F

s− f 0 s− f ' 0



całkowanie oryginału,

L

[

∫

0

t

f

d 

]

=

F

s

s

9

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

różniczkowanie obrazu,

L

[t⋅f t ]=−

d

ds

F

s

całkowanie obrazu,

L

[

1

t

f

t 

]

=

∫

s

∞

F

 zdz

10

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

transformata splotu

L

[ f

1

t ∗ f

2

t ]=F

1

s⋅F

2

s

f

1

t ∗ f

2

t=

∫

0

t

f

1

z⋅f

2

t−zdz

F

s=F

1

s⋅F

2

s

f

1

t =L

−1

[ F

1

s]

f

2

t =L

−1

[ F

2

s]

f

t = f

1

t ∗ f

2

t

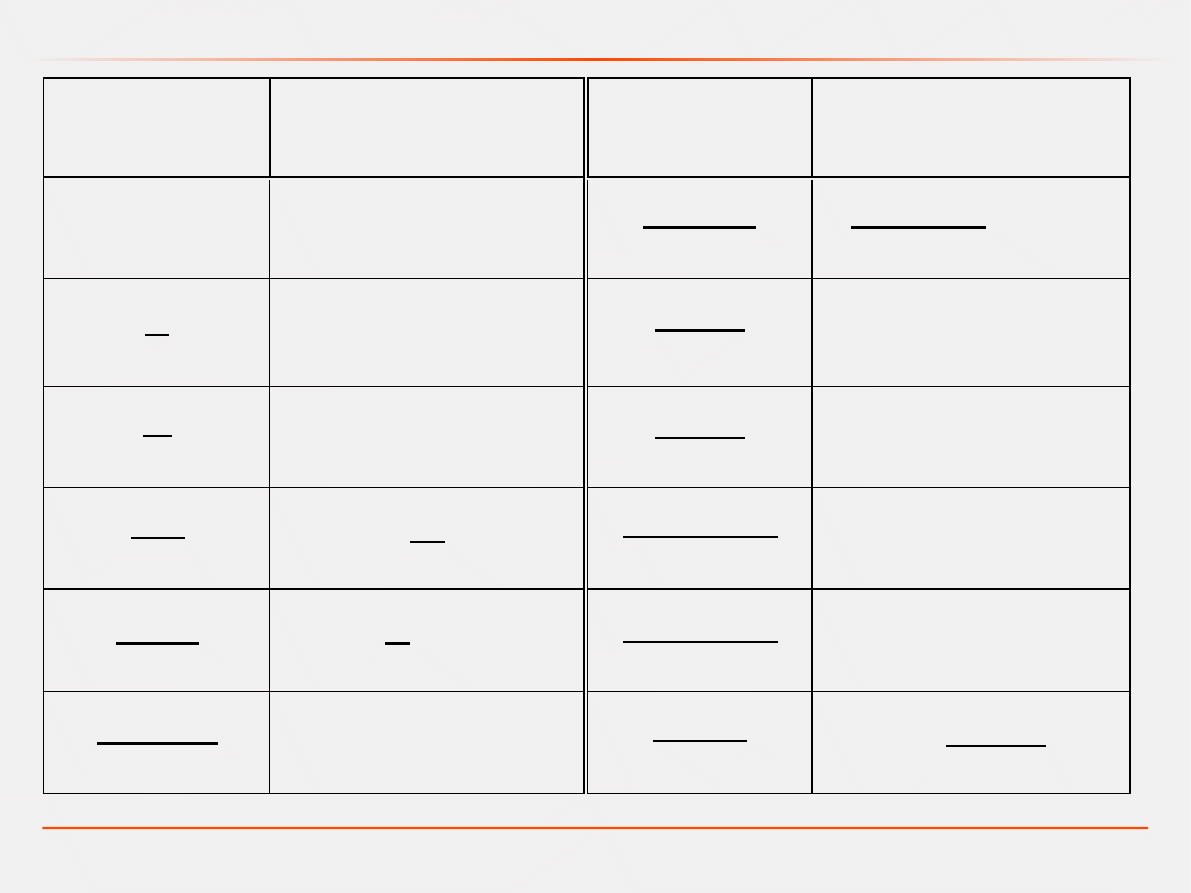
11

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

F(s)

f(t)

F(s)

f(t)

1

t; impuls Diraca

1

1sT 

n

1

1−n! T

n

t

n

−1

e

−t/T

1

s

1



t



=

{

0 ; t

0

1; t

≥0

s

s

2



2

cos

t 

1

s

2

t



s

2



2

sin

 t

1

s

n

1

t

n

n !

s

a

sa

2



2

e

−at

cos

 t

1

1

sT

1

T

e

−t/T



sa

2



2

e

−at

sin

t

1

s

1sT 

1

−e

−t/T

1

sa

n

e

−at

t

n

−1

n−1!

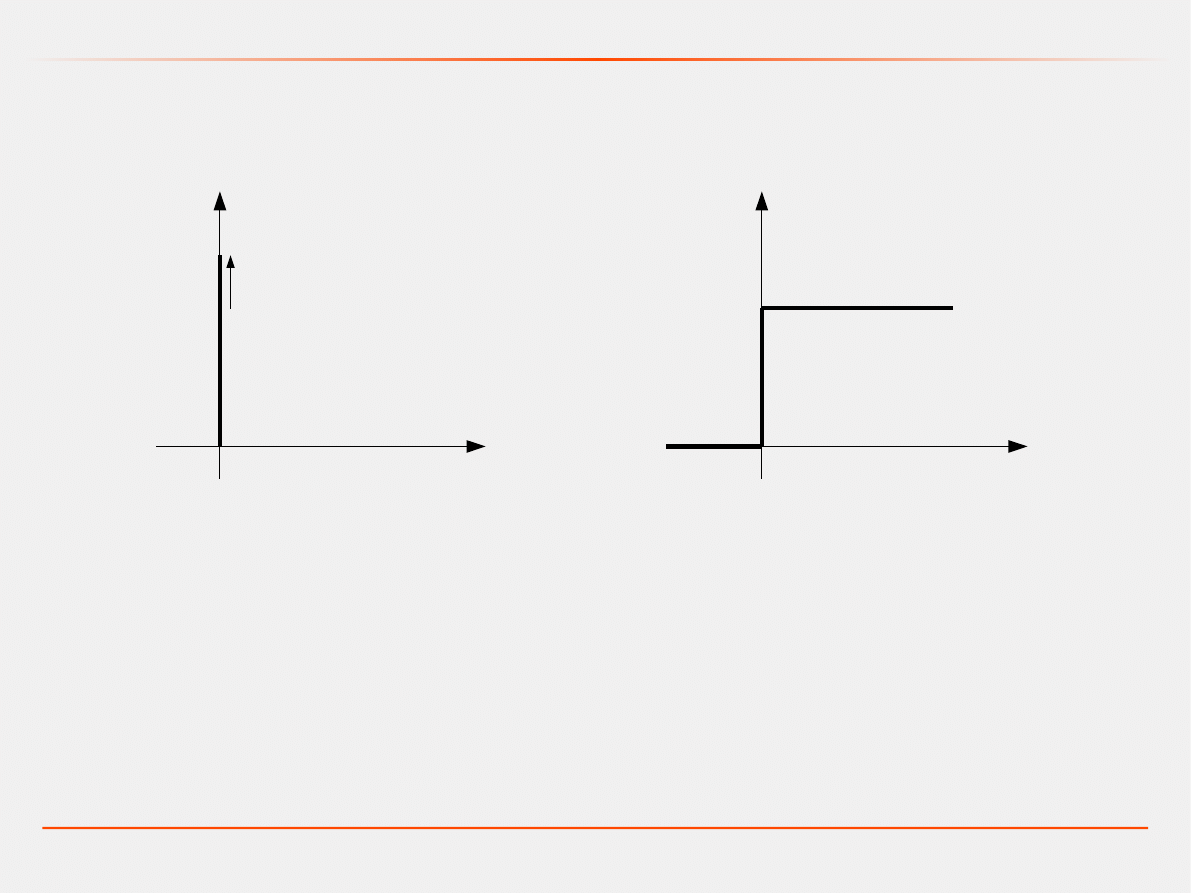
12

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

t

t 

∞

Impuls Diraca

t

1

t 

1

Skok jednostkowy

1

t=

{

0 ; t

0

1 ; t

≥0

t =

{

0 ; t

≠0

∞ ; t=0

13

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

f(t)

F(s)

L[f(t)]

L

-1

[F(s)]

Przykład: obliczanie obrazu F(s) funkcji f(t) z definicji

f

t =e

−2t

F

s=L[e

−2t

]=

∫

0

∞

e

−2t

⋅e

−st

dt

=

∫

0

∞

e

−2st

dt

=

1

−2s

e

−2st

∣

0

∞

F

s=L[e

−2t

]=−

1

−2s

=

0.5

1

0.5s

14

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

Przykład: obliczanie obrazu F(s) funkcji f(t) z wykorzystaniem tabeli

f

t =e

−2t

F

s=L[e

−2t

]=L[e

−t /0.5

]=

0.5

1

0.5s

z tabeli:

L

[a⋅f t]=a⋅F s

f

t =

1

T

e

−t /T

F

s=

1

1

sT

wykorzystując właściwość:

otrzymamy:

f

t =e

−t /T

F

s=

T

1

sT

ostatecznie:

15

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

Rozwiązywanie 

równań 

różniczkowych 

z 

wykorzystaniem 

przekształcenia Laplace'a.

Przykład: Chcemy rozwiązać równanie 

˙0=0

0=1

¨40cdot=0

Przekształcamy równanie w przestrzeń obrazów

L

[ ¨t]=s

2

s−0 s− ˙0=s

2

s−s

L

[40cdot t]=40cdot L[t]=40cdot s

s

2

s−s40cdot s=0

s=

s

s

2

40

t =L

−1

[s]=cos



40 t

16

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Rachunek operatorowy

Wykorzystanie transformaty Laplace'a umożliwia: 

rozwiązywanie równań różniczkowych zwyczajnych o stałych 
współczynnikach,
rozwiązywanie niektórych równań różniczkowych cząstkowych,

rozwiązywanie pewnych klas równań całkowych czy też 
różniczkowo-całkowych,

badanie odpowiedzi impulsowej układu oraz badanie stabilności 
układu.

17

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – opis „wejście-wyjście”

Liniowy  system  dynamiczny  możemy  opisać  za  pomocą 
zwyczajnego  równania  różniczkowego  o  stałych  współczynnikach 
przy zerowych warunkach początkowych:  

a

n

d

n

y

dt

n

a

n

−1

d

n

−1

y

dt

n

−1

a

0y

=b

m

d

m

u

dt

m

b

m

−1

d

m

−1

u

dt

m

−1

b

0u

gdzie:  

n

m

Stosując zapis operatorowy otrzymamy:  

a

n

s

n

a

n

−1

s

n

−1

a

0

Y s=b

m

s

m

b

m

−1

s

m

−1

b

0

U s

18

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

G

s=

Y

s

U

s

=

b

m

s

m

b

m

−1

s

m

−1

b

0

a

n

s

n

a

n

−1

s

n

−1

a

0

Transmitancja  operatorowa  G(s)

 

jest  zdefiniowana  jako 

stosunek transformaty Laplace’a sygnału wyjściowego Y(s) 
do  transformaty  Laplace’a  sygnału  wejściowego  U(s),  przy 
założeniu, że wszystkie warunki początkowe są zerowe.

19

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

Własności transmitancji operatorowej: 

transmitancja 

jest 

własnością

 samego 

systemu, 

niezależnie od wielkości i natury sygnału wejściowego,
transmitancja  przedstawia  związki  pomiędzy  sygnałami 
wyjściowym i wejściowym, nie dostarcza natomiast żadnej 
informacji dotyczącej fizycznej struktury systemu,
transmitancje wielu fizycznie różnych systemów mogą być 
identyczne
łatwość  stosowania  transmitancji  do  tworzenia  modeli  o 
skomplikowanej strukturze

20

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

Właściwości transmitancji operatorowej: 

jeśli transmitancja układu jest znana, to możemy określić 
sygnał wyjściowy dla różnych sygnałów wejściowych,

raz 

określona 

transmitancja 

daje 

pełny 

opis 

charakterystyk  dynamicznych  układu,  w  odróżnieniu  od 
jego opisu fizycznego,

stosując  podstawienie  s=j

ω

 otrzymujemy  transmitancję 

widmową,  znajomość  której  pozwala  na  wyznaczanie 
charakterystyk częstotliwościowych systemu.

21

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

Transmitancja  operatorowa  charakteryzuje  odpowiedź 
modelu  na  pewne  standardowe  sygnały  wejściowe,  np. 
odpowiedź modelu na skok jednostkowy otrzymamy dzieląc 
transmitancję przez operator s.

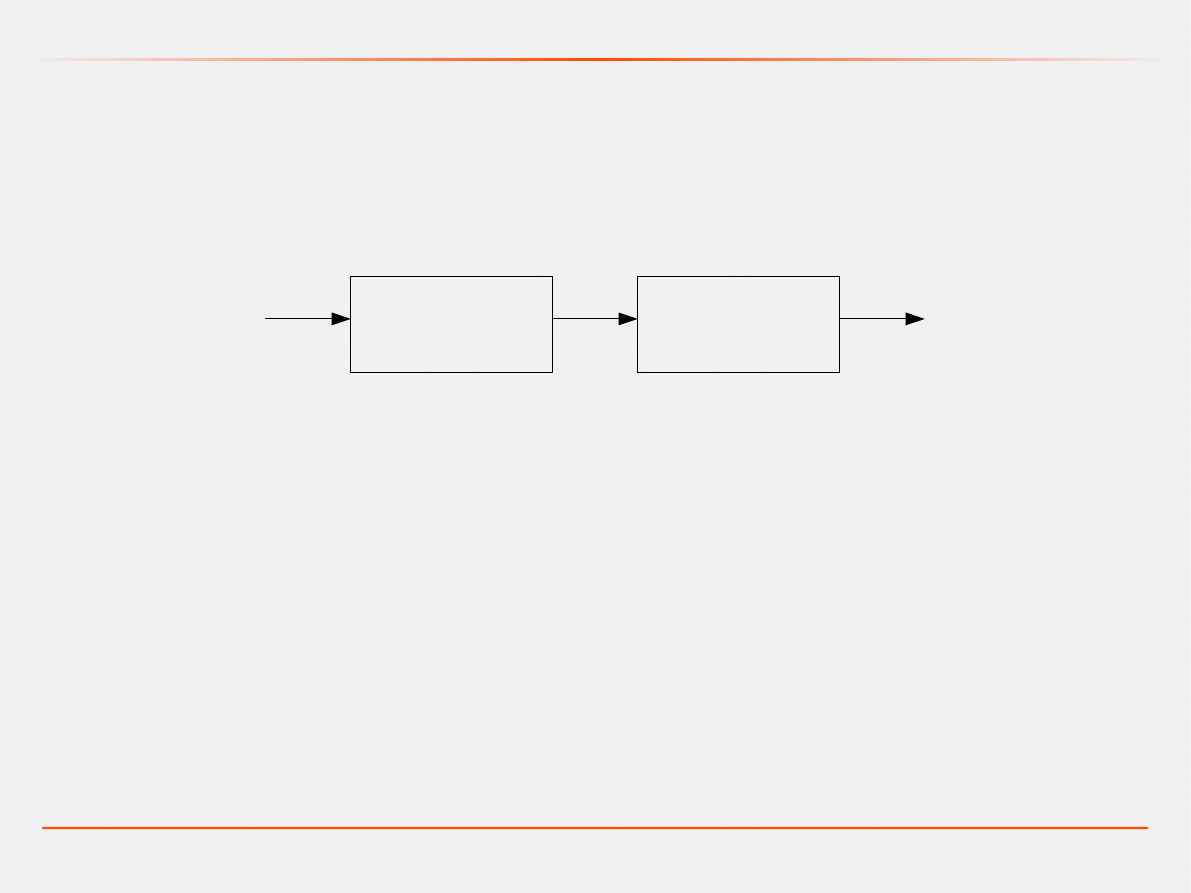
22

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

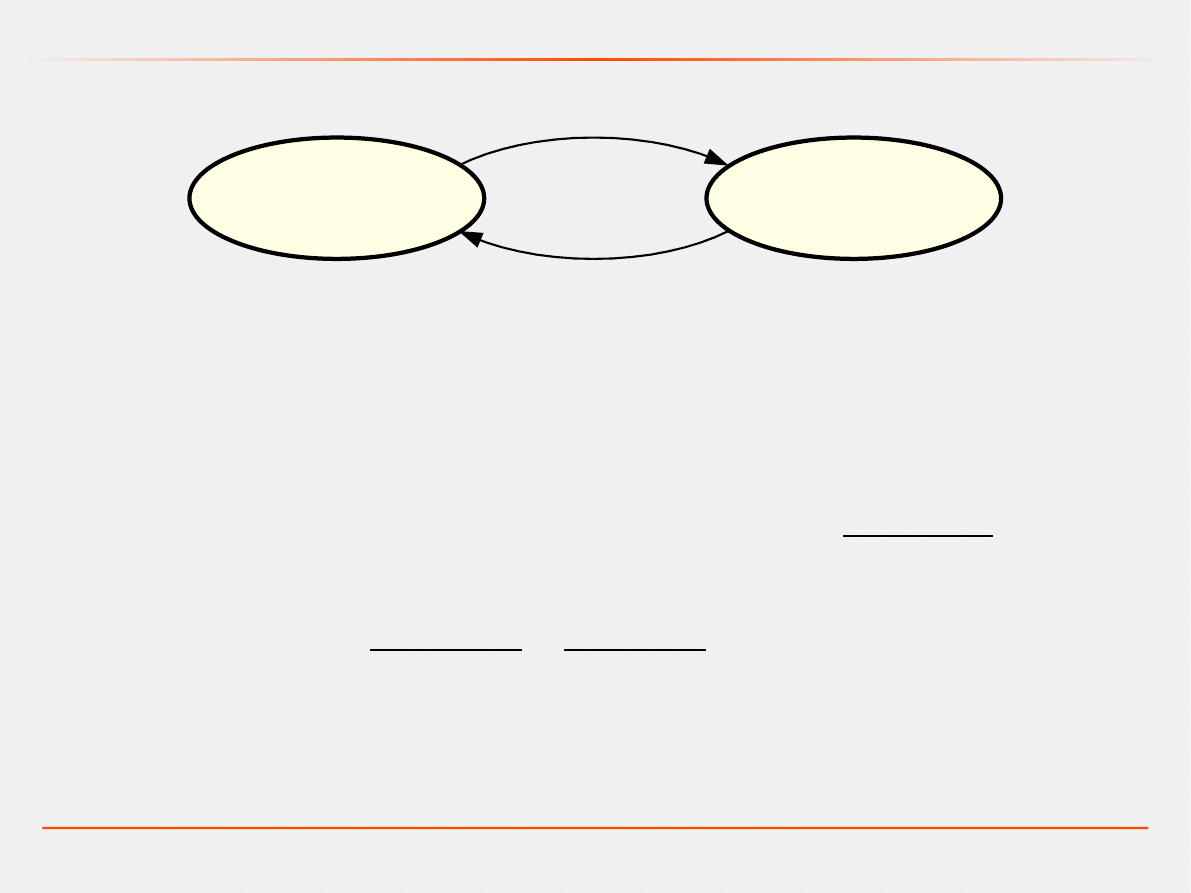
Transmitancje sprzężeń podstawowych.

sprzężenie szeregowe

G

1

(s)

G

2

(s)

G

s=G

1

s⋅G

2

s

Ze  względu  na  nieprzemienność  operacji  mnożenia 

operatorów  kolejność  połączenia  szeregowego  ma  istotne 

znaczenie!

23

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

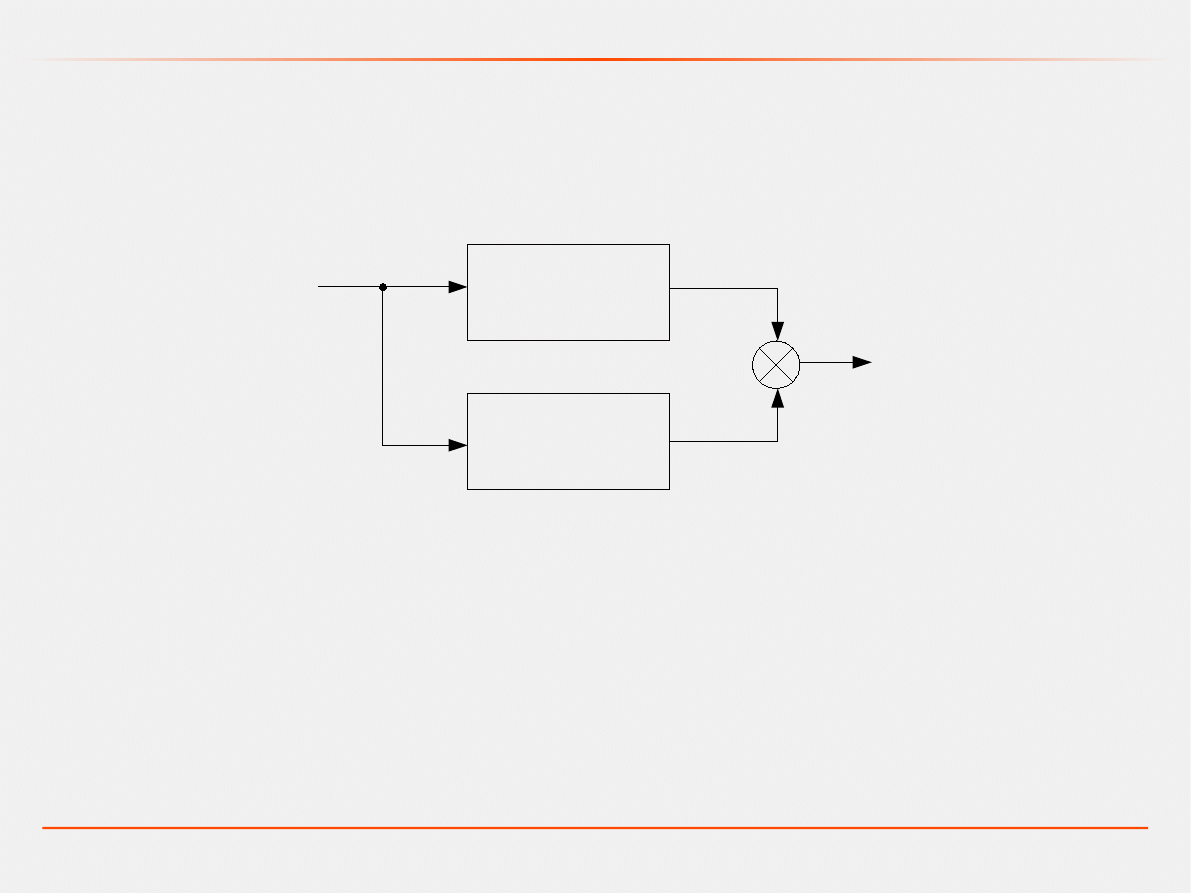
Model dynamiczny – transmitancja operatorowa

sprzężenie równoległe

G

1

(s)

G

2

(s)

+

+

G

s=G

1

sG

2

s

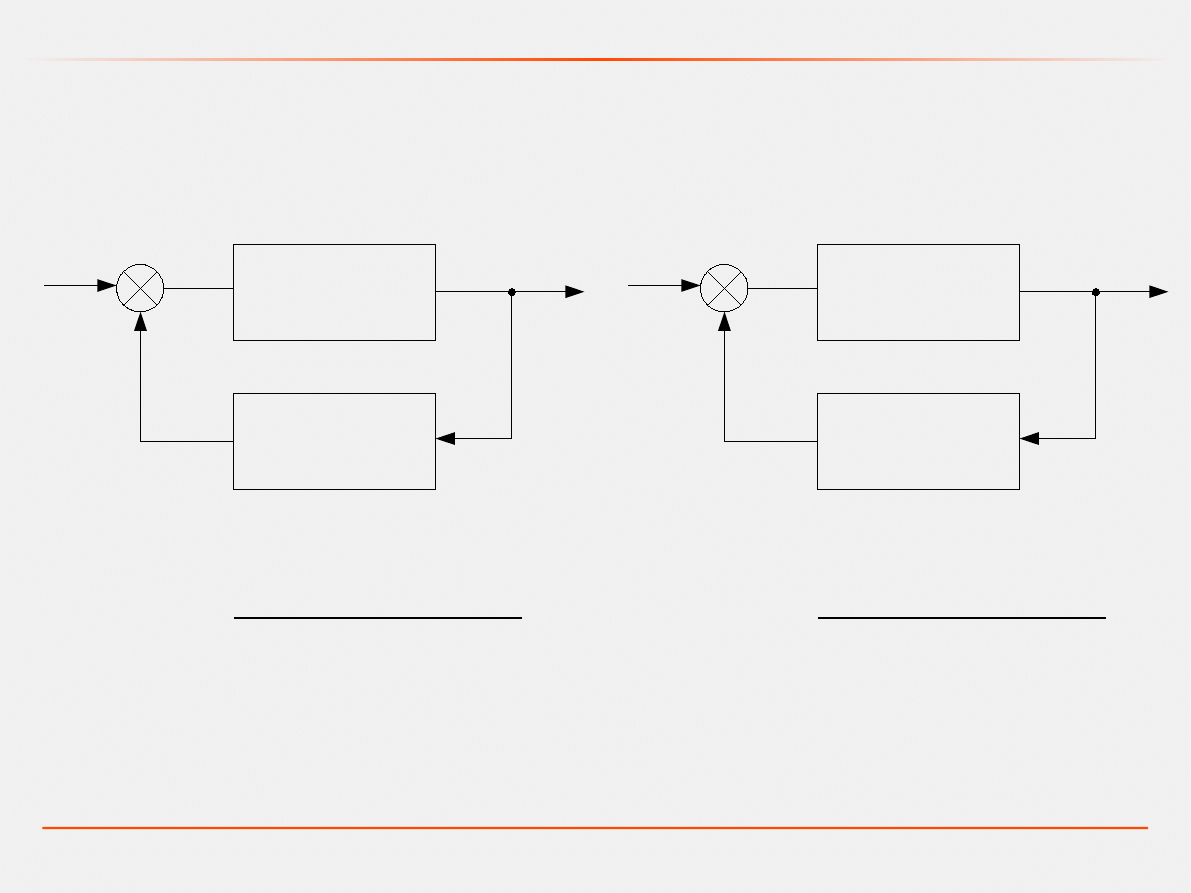
24

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

sprzężenia zwrotne

G

1

(s)

G

2

(s)

+

+

G

s=

G

1

s

1

−G

1

s⋅G

2

s

G

1

(s)

G

2

(s)

+

-

G

s=

G

1

s

1

G

1

s⋅G

2

s

25

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

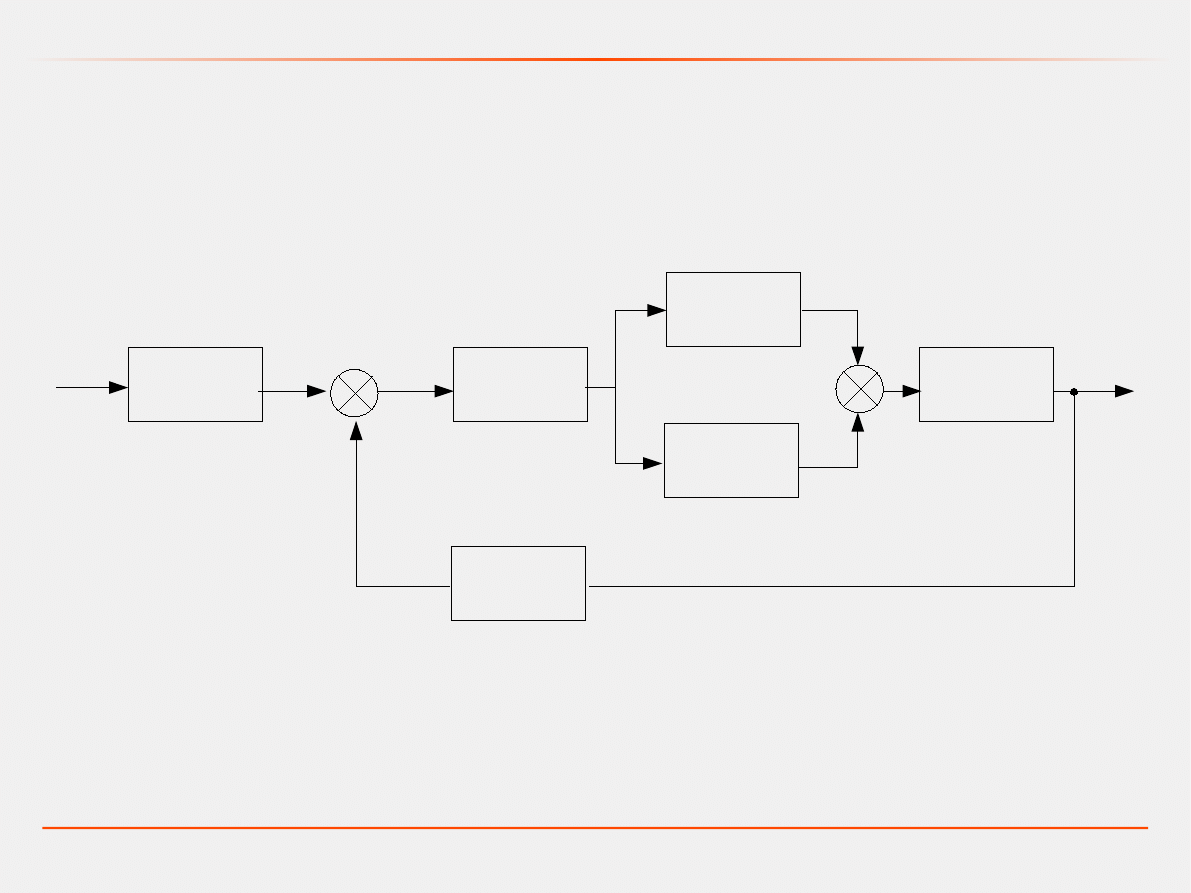
A jak to będzie dla przedstawionego układu?

G

1

(s)

+

G

2

(s)

G

3

(s)

G

4

(s)

G

5

(s)

G

6

(s)

+

+

-

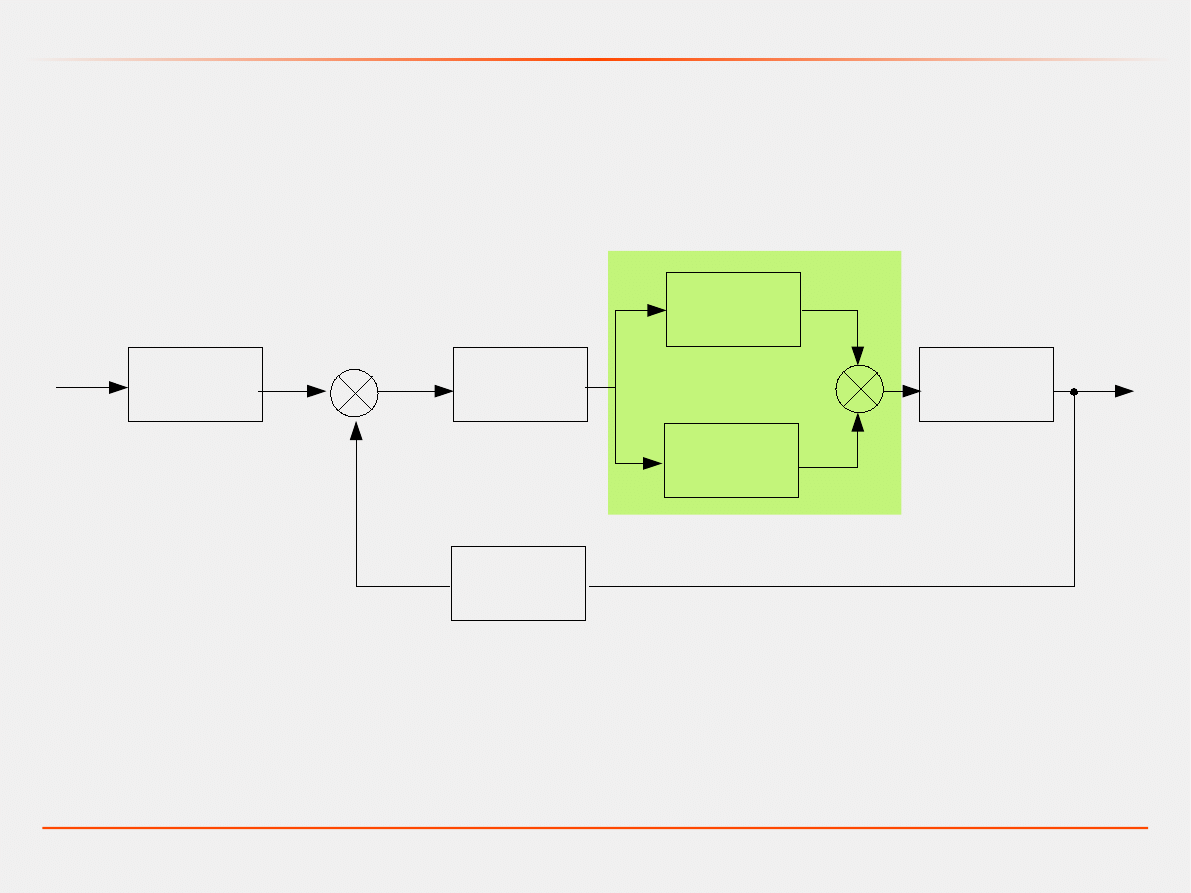
26

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

A jak to będzie dla przedstawionego układu?

G

1

(s)

+

G

2

(s)

G

3

(s)

G

4

(s)

G

5

(s)

G

6

(s)

+

+

-

G

34

=G

3

−G

4

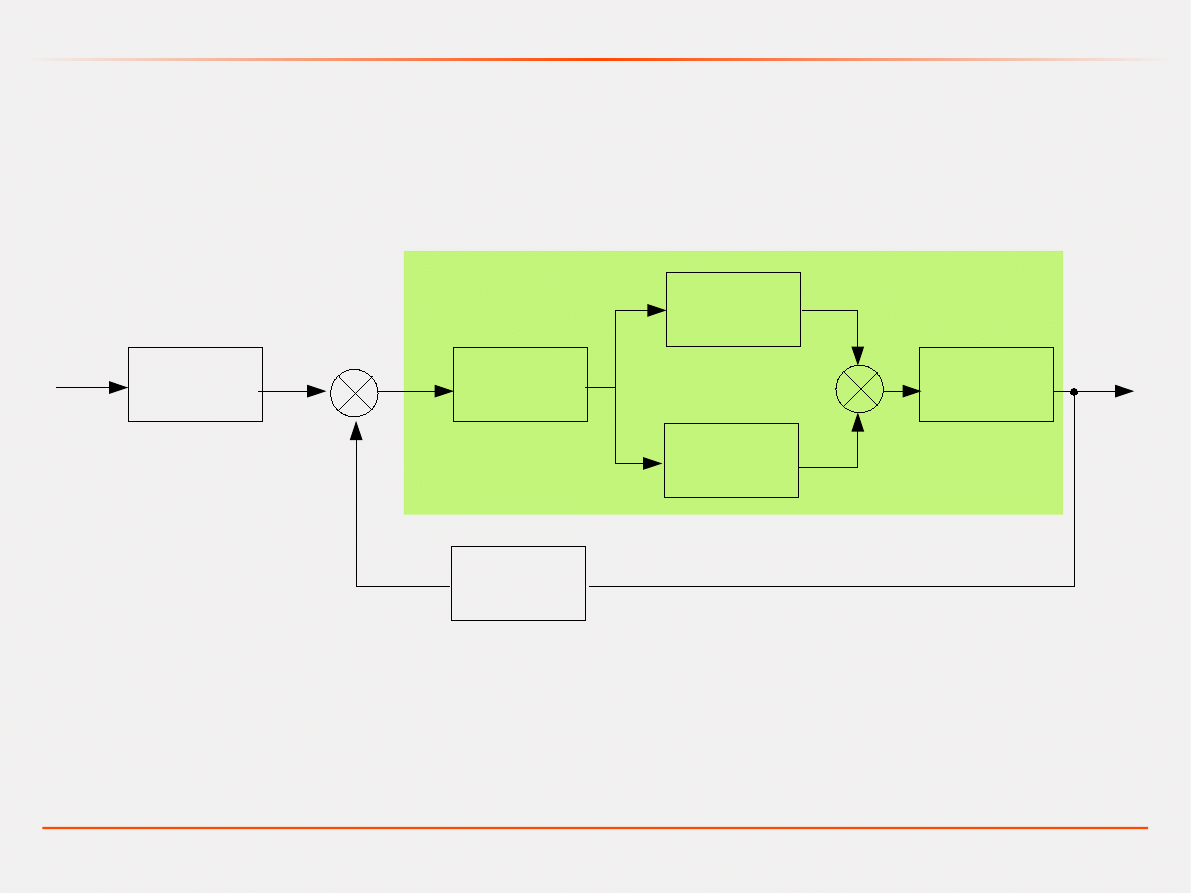
27

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

A jak to będzie dla przedstawionego układu?

G

1

(s)

+

G

2

(s)

G

3

(s)

G

4

(s)

G

5

(s)

G

6

(s)

+

+

-

G

25

=G

2

⋅G

3

−G

4

⋅G

5

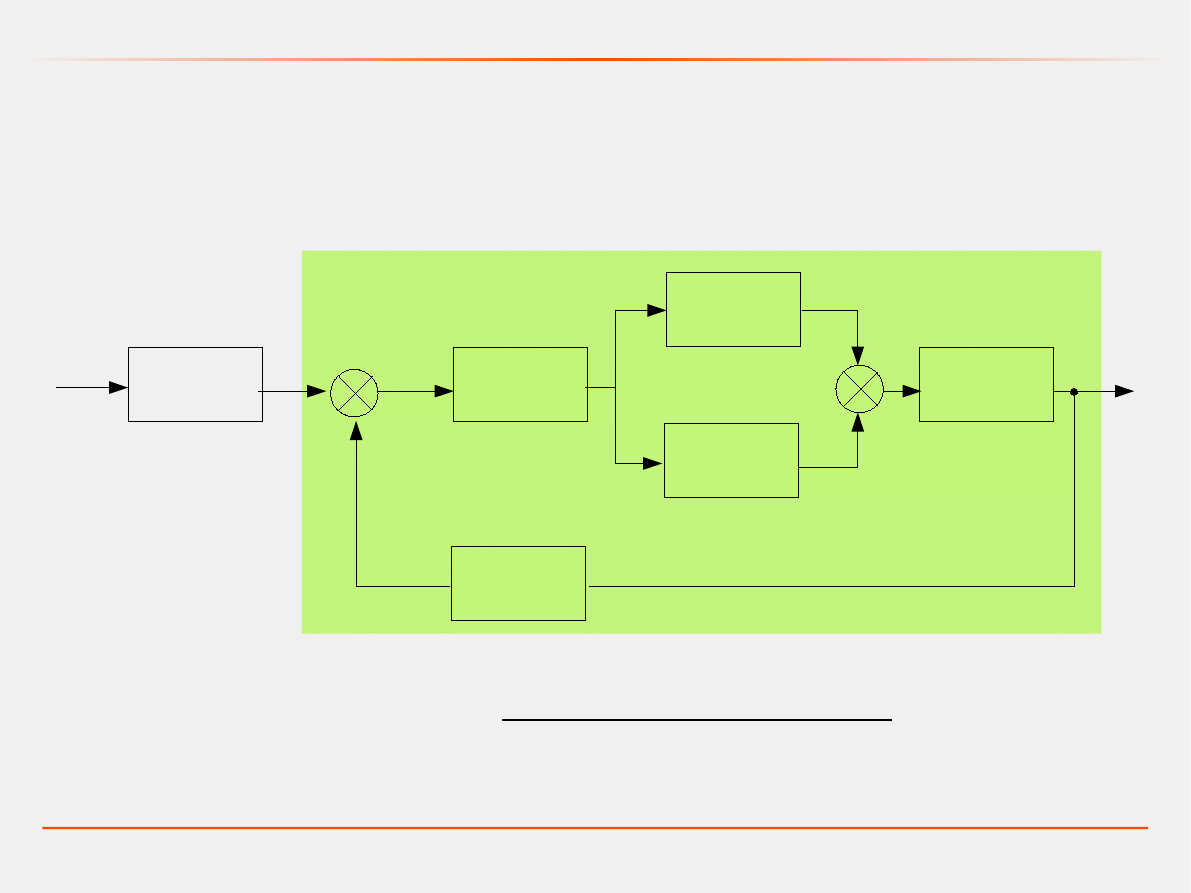
28

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

A jak to będzie dla przedstawionego układu?

G

1

(s)

+

G

2

(s)

G

3

(s)

G

4

(s)

G

5

(s)

G

6

(s)

+

+

-

G

26

=

G

2

G

3

−G

4

G

5

1

−G

6

G

2

G

5

G

3

−G

4



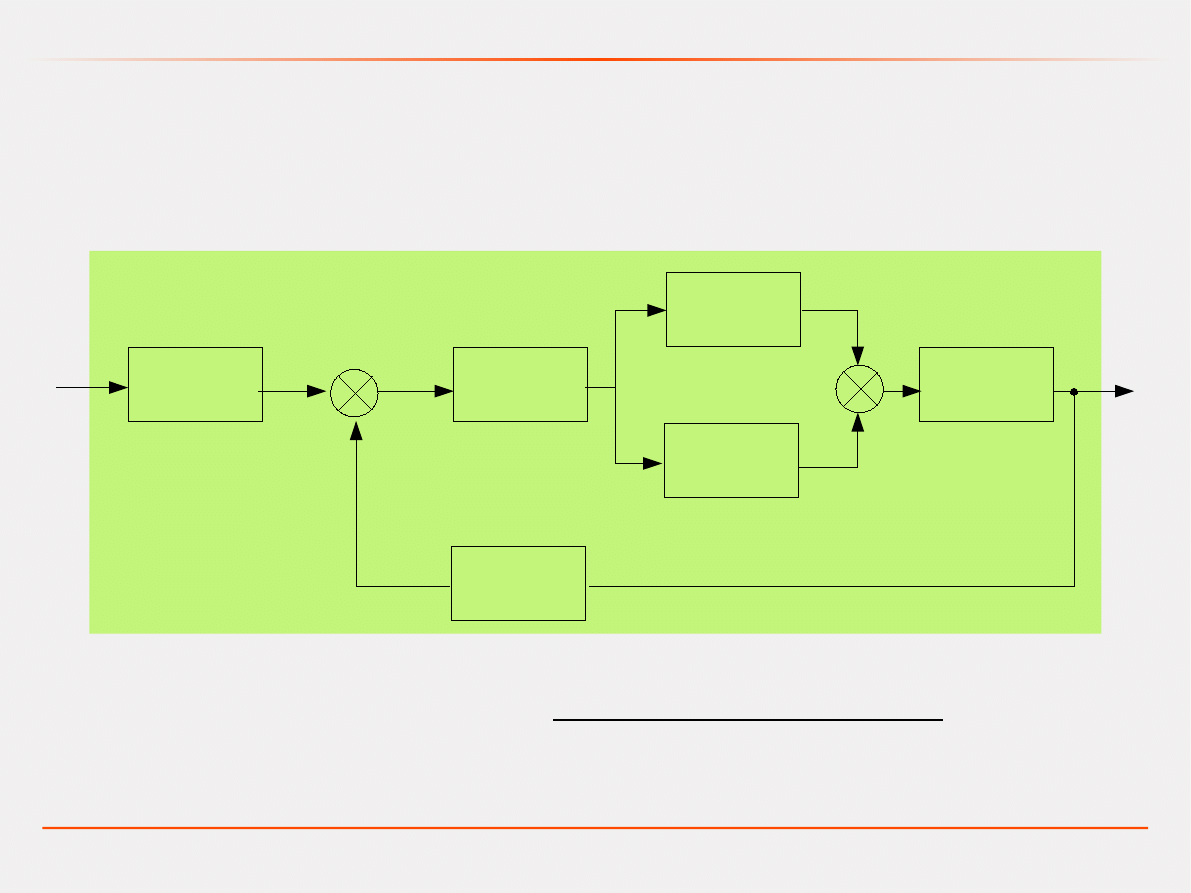
29

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa

A jak to będzie dla przedstawionego układu?

G

1

(s)

+

G

2

(s)

G

3

(s)

G

4

(s)

G

5

(s)

G

6

(s)

+

+

-

G

=G

1

G

2

G

5

⋅

G

3

−G

4

1

−G

2

G

5

G

6

G

3

−G

4

