1

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Modelowanie i symulacja

dr inż. Piotr Piela

Zakład Matematyki Stosowanej

kontakt: pokój 28 

ppiela@wi.ps.pl

2

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Literatura

Guntenbaum Jakub – Modelowanie matematyczne systemów, 

Akademicka Oficyna Wydawnicza EXIT, Warszawa, 2003
Banks  Jerry  –  Handbook  of  simulation,  John-Wiley  and  Sons 

Inc., New York, 1998
Klempka  Ryszard,  Stankiewicz  Antoni  –  Modelowanie 
i symulacja  układów  dynamicznych,  Uczelniane  Wydawnictwo 

Naukowo-Dydaktyczne AGH, Kraków, 2004
Morrison 

Foster 

– 

Sztuka 

modelowania 

układów 

dynamicznych, WNT, Warszawa, 1996
Szacka  Krystyna  –  Teoria  układów  dynamicznych,  Oficyna 

Wydawnicza Politechniki Warszawskiej, Warszawa, 1999

3

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

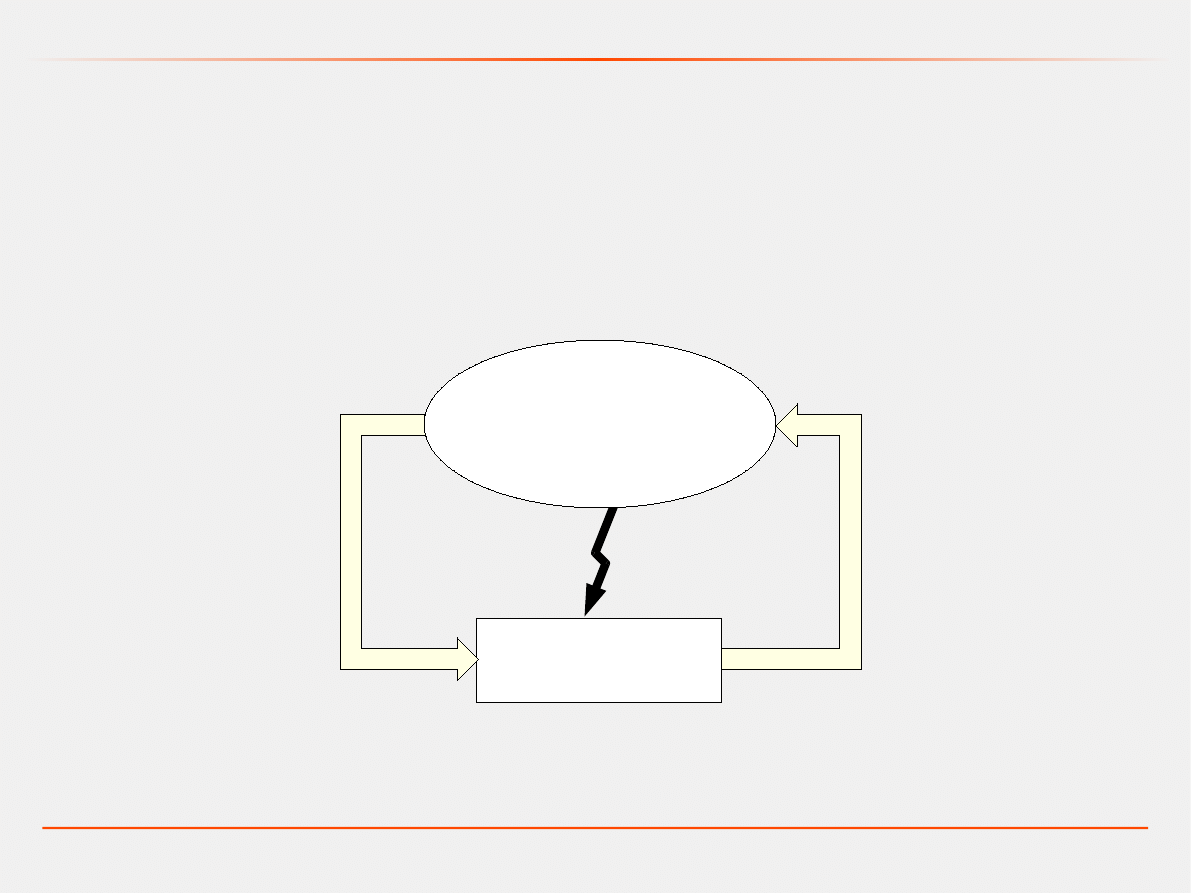
Wprowadzenie

Przystępując do badania jakiegoś obiektu lub zjawiska stanowiącego 

część  otaczającej  nas  rzeczywistości  musimy  tę  część  przede 
wszystkim określić, czyli wyodrębnić z otoczenia. Taka część będzie 
dalej określana jako system (system = układ).

SYSTEM

OTOCZENIE

WIELKOŚCI

WEJŚCIOWE

WIELKOŚCI

WYJŚCIOWE

ZAKŁÓCENIE

4

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

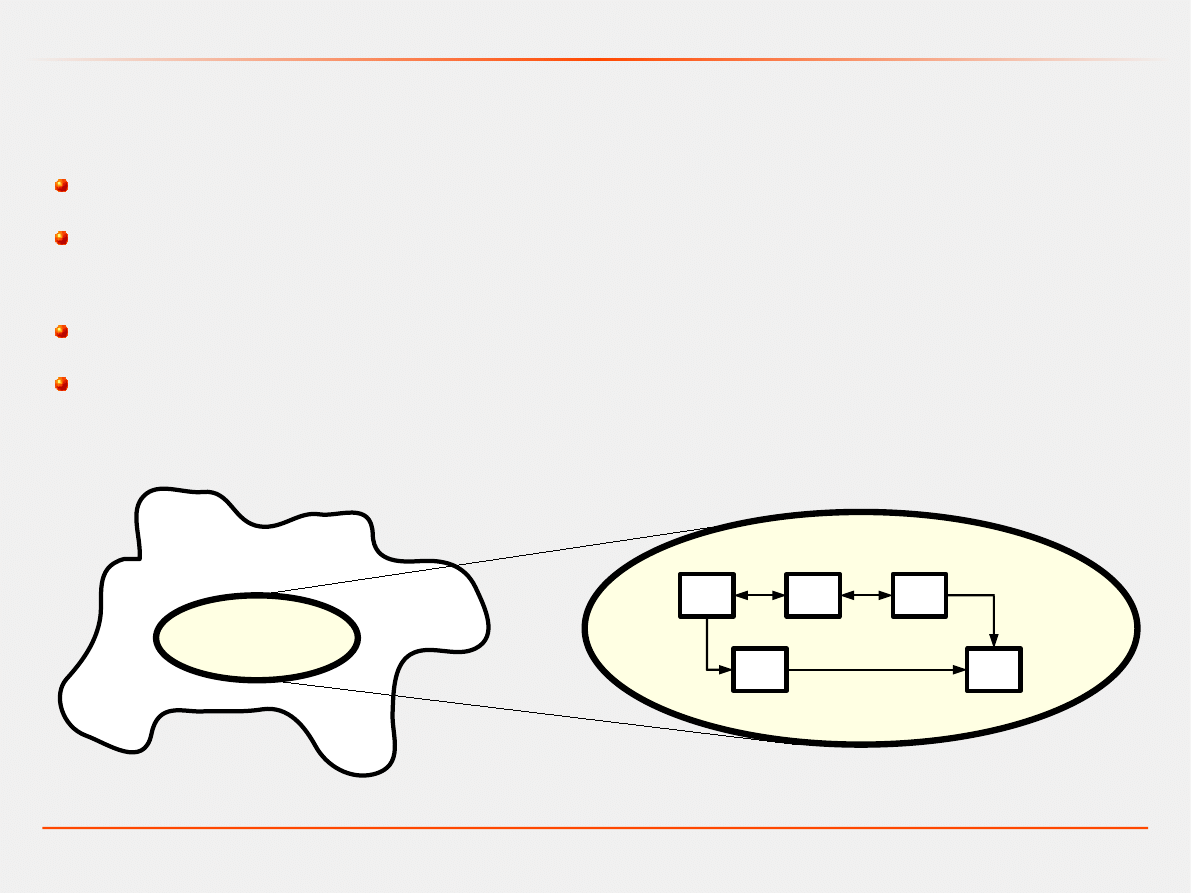
System powinien spełniać 4 podstawowe postulaty:

 wyodrębnienie z otoczenia,
budowa z podsystemów, które oddziałują na siebie wzajemnie przy 
czym oddziaływania te maja istotny wpływ na własności systemu,
spełnianie celu założonego działania,
ograniczoność zmienności w czasie – zachowuje swoje 
podstawowe właściwości.

OTOCZENIE

SYSTEM

P1

P2

P3

P4

P5

SYSTEM

Wprowadzenie

5

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Wprowadzenie

Aby  zrozumieć  działanie  systemu  buduje  się  jego  modele.  Stosując 
modele 

obserwujemy

 i 

sprawdzamy

,  jakie  prawa  rządzą 

systemami.  Jeśli  zrozumiemy  te  prawa  to  możemy  przewidzieć  jak 
system zachowa się w przyszłości w innych warunkach.

Model  trzeba  zawsze  tworzyć  dla  konkretnego  systemu  i  do 

konkretnych zastosowań.
Przykład:

jeśli samolot przedstawimy jako nieodkształcalną bryłę sztywną, to 

nie będzie możliwa analiza drgań konstrukcji samolotu,
jeśli w rurociągu pominiemy zjawiska tarcia i lepkości cieczy, nie 
będzie możliwa analiza cieplna.

6

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Model 

w  nauce  jest  rozumiany  jako  uproszczona  –  przy  czym 

umyślnie  i  celowo  –  reprezentacja  rzeczywistości,  ujmuje  tylko  jej 

część,  jest  pozbawiony  wielu  szczegółów  i  cech  nieistotnych  z 
punktu widzenia celów modelowania.

Model w sztuce może być lepszy niż rzeczywisty obiekt.

Model  uwzględnia  tylko  wybrane  czynniki  wpływające  i  tylko  w 
ograniczonym  zakresie  zmienności.  Zakres  uwzględnianych  zjawisk 

zależy od dostępnej wiedzy i celu badań symulacyjnych.

Wprowadzenie

7

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Wprowadzenie

Cele budowy modeli systemów:

opis  i  wyjaśnienie  mechanizmu  działania  systemu  (modele 
fenomenologiczne / systemy biologiczne),

przewidywanie  zachowania  się  systemów    w  przyszłości  i  przy 
różnorodnych  warunkach  działania  otoczenia  na  system  (modele 

prognostyczne / systemy ekonomiczne),

wybór  właściwych  oddziaływań  wejściowych,  spełniających 
określone warunki (modele decyzyjne / systemy sterowania),

wybór  struktury  lub  parametrów  systemu,  spełniającego  określone 
zadania (modele normatywne / systemy techniczne)

8

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Rodzaje modeli:

lingwistyczne (opis słowny),
graficzne (np. schemat obwodu, wykresy charakterystyk),
budowane z elementów fizycznych,
matematyczne.

Model matematyczny

 – zbiór symboli i relacji matematycznych oraz 

bezwzględnie ścisłych zasad operowania nimi, przy czym zawarte w 
modelu  symbole  i  relacje  mają  interpretację  odnoszącą  się  do 
konkretnych elementów modelowanego wycinka rzeczywistości.

Wprowadzenie

9

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Wprowadzenie

Przykład opisu systemu pomiarowego za pomocą 

poszczególnych rodzajów modeli

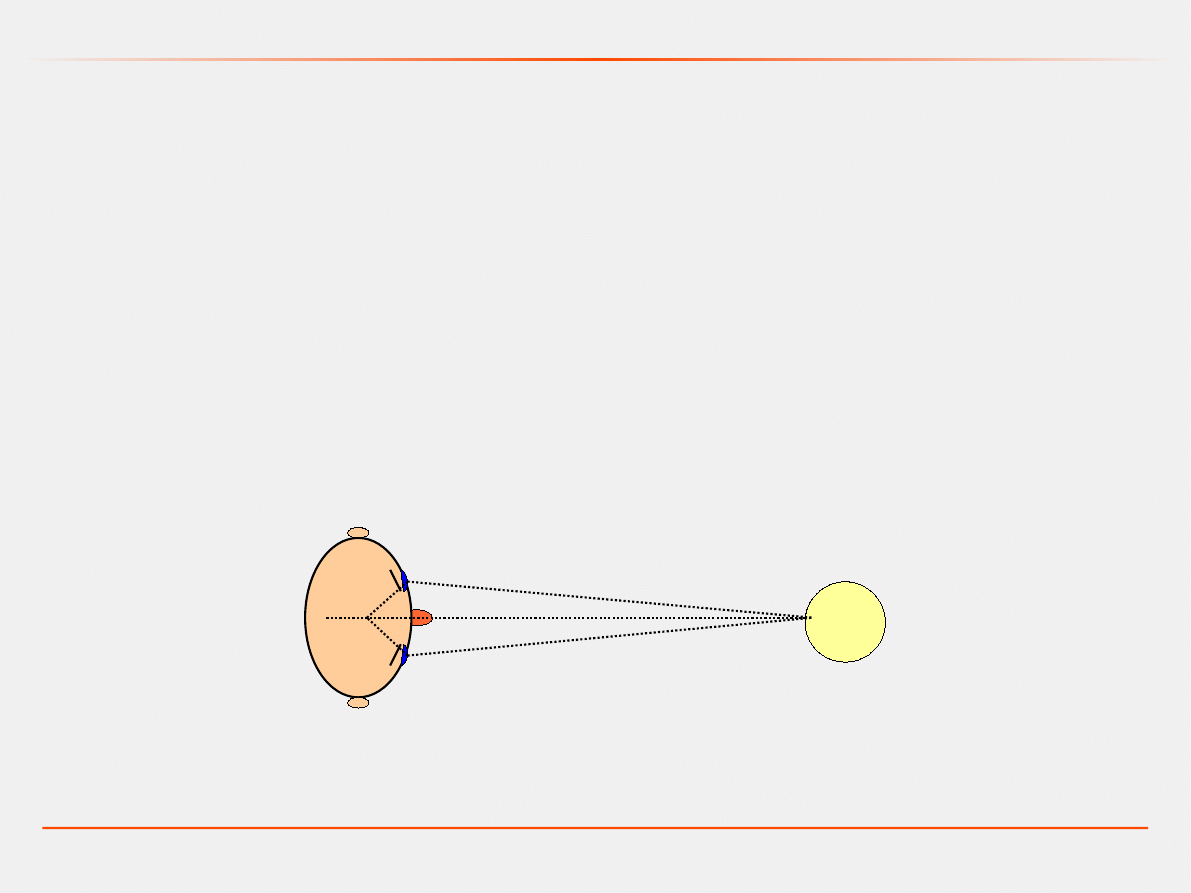
Modelowanym  systemem  pomiarowym  jest  ludzki  narząd  wzroku, 
którego  cechą  interesującą  nas  w  tej  analizie  jest  jego  zdolność  do 

szacowania  odległości  przedmiotów  i  dokładność  takiego 
oszacowania.

10

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Model  lingwistyczny

:  człowiek  jest  w  stanie  oszacować  odległość 

przedmiotu  dzięki  określonemu  ułożeniu  gałek  ocznych.  Kiedy 

przedmiot  jest  odległy,  to  dokładność  oszacowania  jest  mała 
(±5 metrów przy 20 metrach). Kiedy przedmiot jest bliżej to wzrasta 

dokładność  (±10  cm  przy  1  metrze).  Zdolność  szacowania  zanika 
przy bardzo małych odległościach (<10 cm).

Wprowadzenie

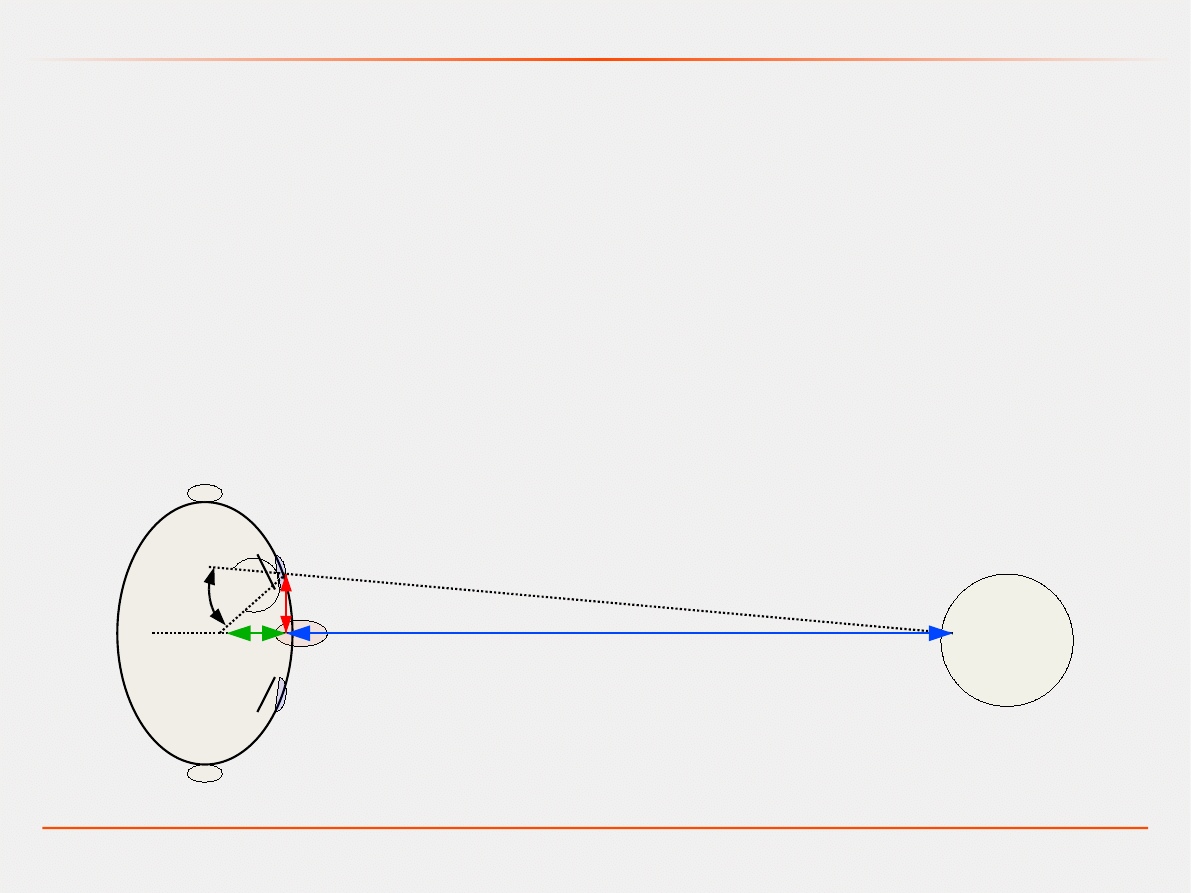
Model graficzny

:

€

11

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Wprowadzenie

Model fizyczny

: makieta ze sklejki i listewek.

Model matematyczny

: Dla stałego kąta załamania 

φ

 i rozstawu oczu 

2z odległość przedmiotu x i odległość odwzorowana x’ są powiązane 

zależnością  trygonometryczną.  Czułość  S  systemu  pomiarowego 
zdefiniowaną jako S=dx’/dx można wyznaczyć przez różniczkowanie 
tej zależności. Dla x mniejszego od pewnej wartości granicznej x’ ma 

wartość nieskończoną (zanika zdolność odwzorowania).

€

x

x'

z

Φ

12

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Wprowadzenie

Modelowanie

 to doświadczalna lub matematyczna metoda badania 

złożonych układów, zjawisk i procesów na podstawie konstruowania 
modeli. 

Modelowanie  doświadczalne

 opiera  się  na  podobieństwie 

fizycznym  (np.  badania  aerodynamiczne)  lub  na  analogiach 

fizycznych (modele elektryczne).

Modelowanie  matematyczne

 polega  na  tworzeniu  modeli 

matematycznych  i  wykorzystaniu  aparatu  matematycznego  do  ich 

analizy.  Zastosowanie  w  tej  analizie  znajdują  komputery  (symulacja 
komputerowa).

13

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Wprowadzenie

Symulacja  komputerowa  – 

odtworzenie  działania  badanego 

systemu rzeczywistego na podstawie jego modelu matematycznego 

za  pomocą  komputera  oraz  zbadanie  wpływu  otoczenia  (zmienne 
wejściowe) i wewnętrznych właściwości systemu (parametry modelu) 

na charakterystyki systemu.

Symulacja  komputerowa  jest  szeroko  stosowana  w  modelowaniu 
wielu  procesów  w  fizyce,  chemii  i  biologii,  ekonomii  oraz  naukach 
społecznych 

(np. 

zachowanie 

tłumu) 

ze 

szczególnym 

uwzględnieniem działania tych procesów.

14

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

Zalety i wady symulacji komputerowej:

łatwość wprowadzania różnego rodzaju wymuszeń i zakłóceń, w 

szczególności losowych,
badanie stanów ekstremalnych,
łatwość wprowadzania zmian w modelu symulowanego systemu
łatwość uzupełniania modelu o nowe zjawiska,
stosunkowo niewielki koszt i czas przygotowania symulacji w 
porównaniu z budową systemu rzeczywistego,
wiarygodność wyników symulacji – szczególnie w tych 
przypadkach, gdy możemy porównać otrzymane wyniki symulacji z 

danymi otrzymanymi z rzeczywistego systemu,
możliwość sterowania czasem symulacji (wydłużanie i skracanie),
rezultaty symulacji mogą być trudne do zidentyfikowania.

Wprowadzenie

15

MODELOWANIE I SYMULACJA

Szczecin - 23.11.2008

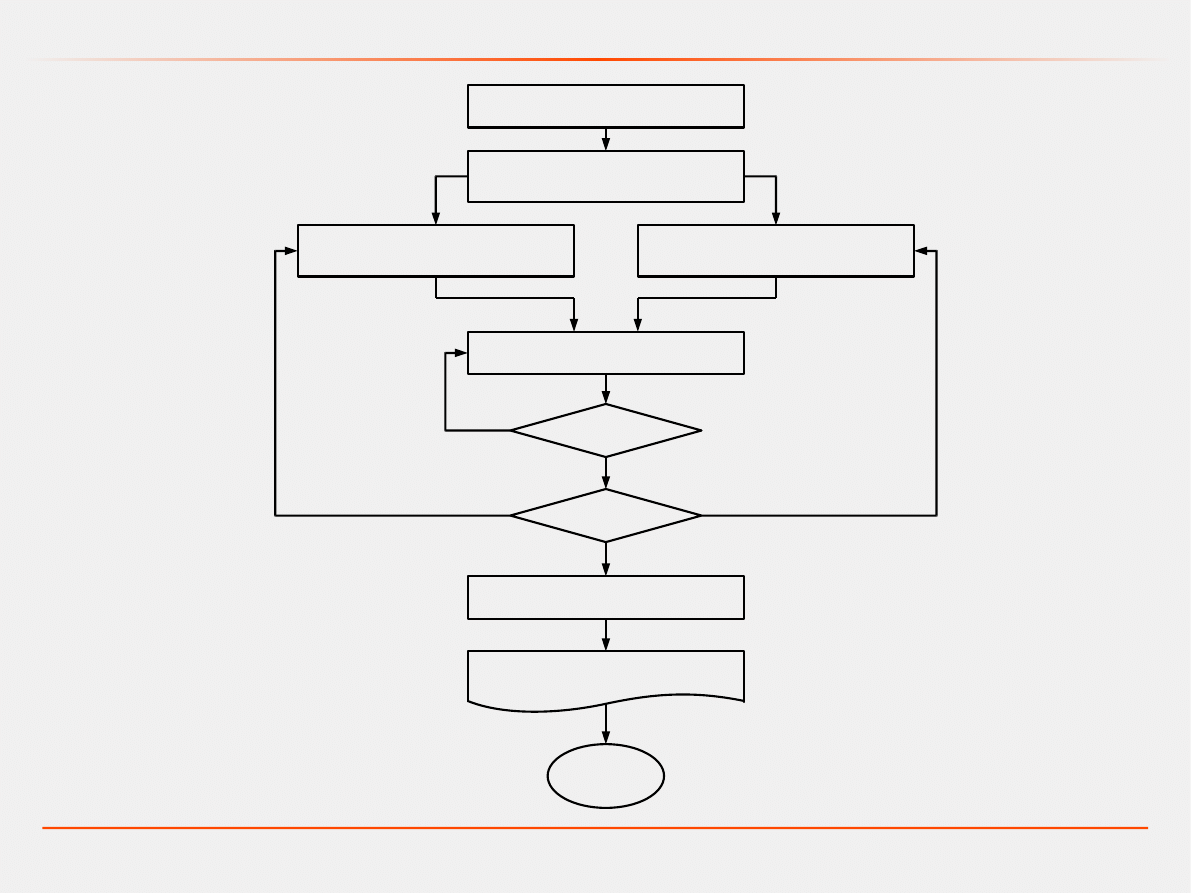
Sformułowanie problemu

Ustalenie celów

 i planu działania

Zbieranie danych

Tworzenie modelu 

konceptualnego

Kodowanie modelu

Testowanie

Nie

Wdrożenie

Tworzenie dokumentacji

 i raportów

Weryfikacja

Walidacja

Nie

Nie

 Tak

 Tak

Proces modelowania