1

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Modelowanie i symulacja

dr inż. Piotr Piela

Zakład Metod Matematycznych

kontakt: pokój 28 

ppiela@wi.ps.pl

2

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

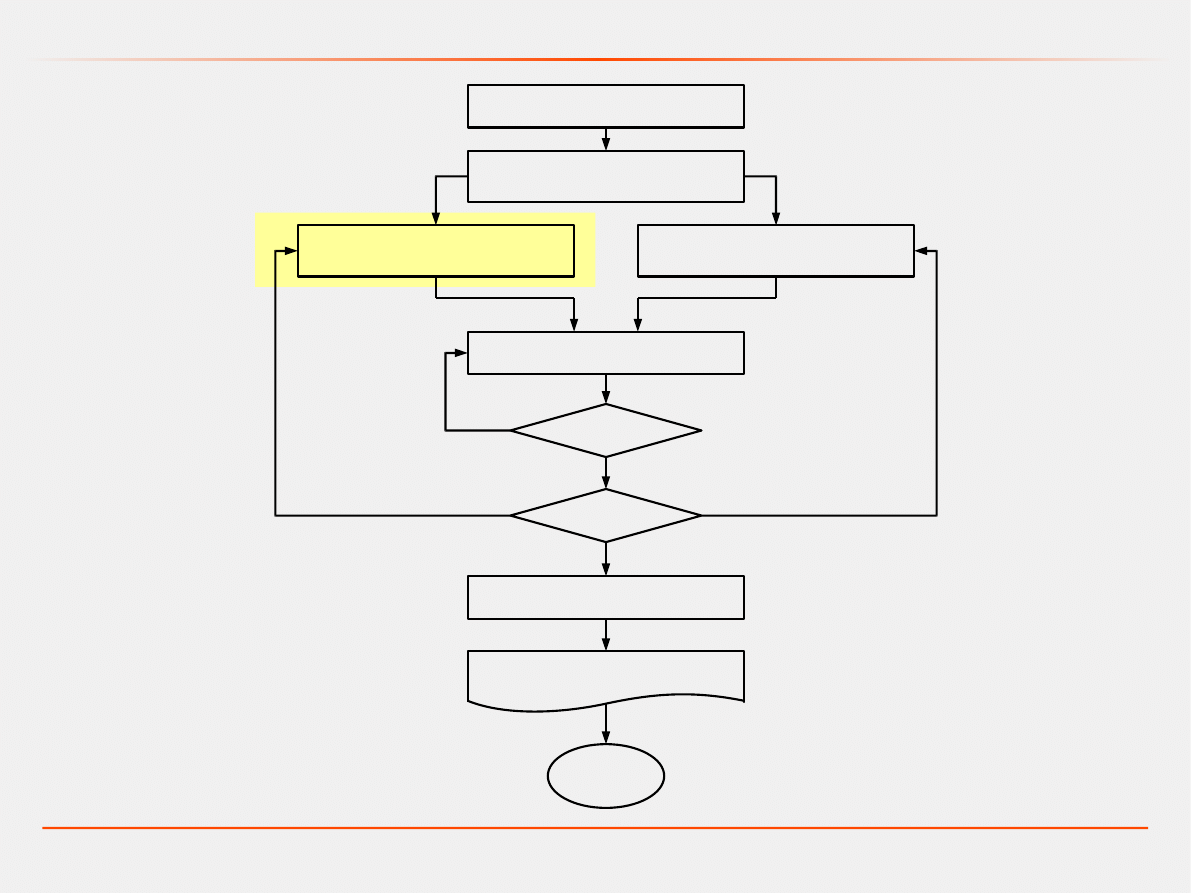
Proces modelowania

Sformułowanie problemu

Ustalenie celów

 i planu działania

Zbieranie danych

Tworzenie modelu 

konceptualnego

Kodowanie modelu

Testowanie

Nie

Wdrożenie

Tworzenie dokumentacji

 i raportów

Weryfikacja

Walidacja

Nie

Nie

 Tak

 Tak

3

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Proces modelowania

Model  dynamiczny  – 

model,  w  którym  wyjście  y  zależy

od  wartości  wejścia  u  w  całym  nieskończonym 

poprzedzającym przedziale czasowym.

y (u, t) = y {u(τ) : −∞ < τ ≤ t}

4

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Stanem  systemu 

nazywamy  najmniejszą  liczbę  danych,  których 

znajomość  w  danej  chwili,  przy  znajomości  wielkości  wejściowych, 

począwszy  od  tej  chwili  –  pozwala  jednoznacznie  określić  stan  i 

wielkości wyjściowe systemu w przyszłości. 

Y=[y

1

 y

2

 ... y

m

]

T

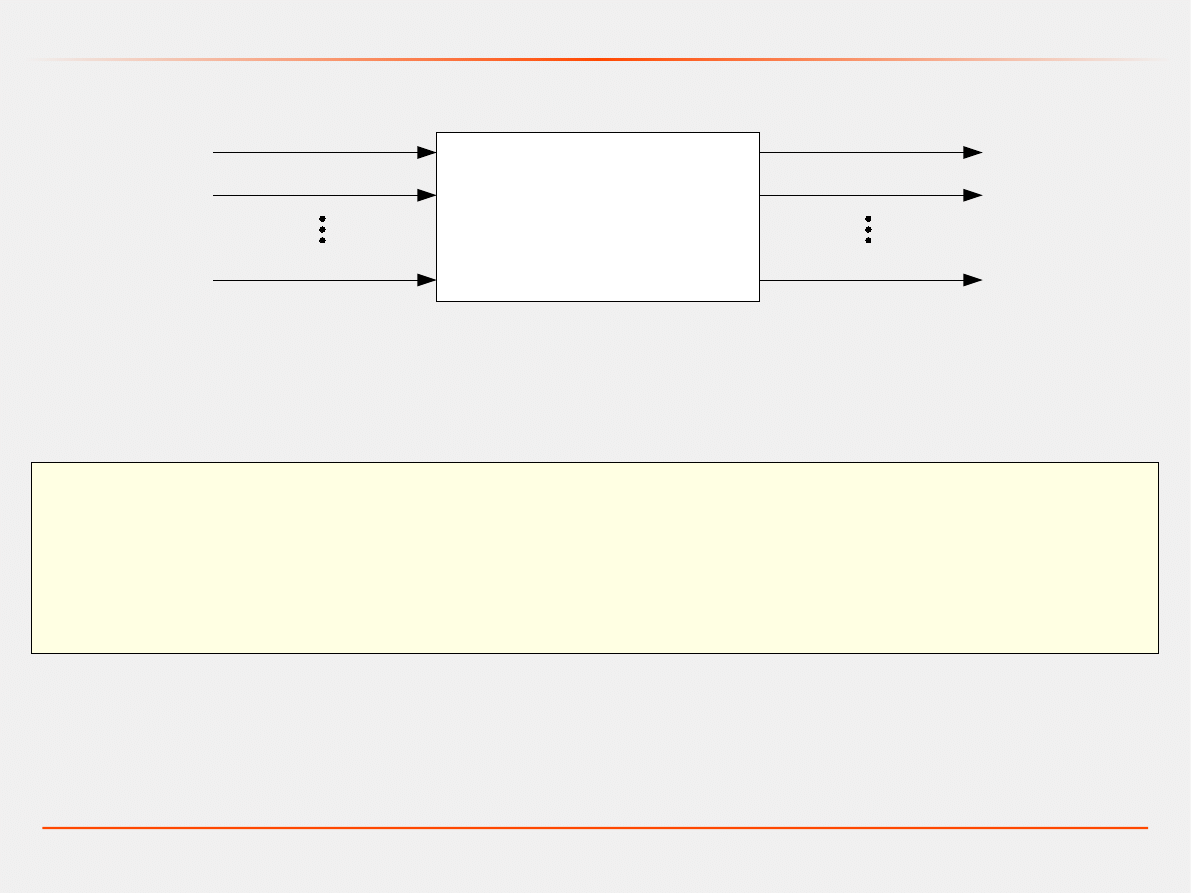
Stanem  systemu 

nazywamy  najmniejszą  liczbę  danych,  których 

znajomość  w  danej  chwili,  przy  znajomości  wielkości  wejściowych, 

począwszy  od  tej  chwili  –  pozwala  jednoznacznie  określić  stan  i 

wielkości wyjściowe systemu w przyszłości. 

SYSTEM

WIELKOŚCI

WEJŚCIOWE

WIELKOŚCI

WYJŚCIOWE

u

1

u

2

u

n

y

1

y

2

y

m

U=[u

1

 u

2

 ... u

n

]

T

Model dynamiczny

5

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny

Wielkości  charakteryzujące  stan  systemu  reprezentowane  są  przez 

zmienne stanu,  których zbiór przedstawiany jest w postaci 

wektora 

stanu

. 

Przestrzeń stanów

 – n-wymiarowa przestrzeń, w której każdy stan 

może być przedstawiony jako punkt w tej przestrzeni.

Zmienne  stanu

 to  zestaw  zmiennych,  których  znajomość  w  danej 

chwili  t  zawiera  całą  informację  o  przeszłości  systemu,  przy  czym 

powinien to być zestaw o minimalnej liczbie zmiennych.

X=[x

1

 x

2

 ... x

n

]

T

6

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny

Ten  sam  system  może  być  opisany  przez  różne  zbiory  zmiennych 

stanu.
Oprócz  zmiennych  stanu  rozpatruje  się  dodatkowo  zewnętrzne 

zaburzenia,  które  w  znacznym  stopniu  wpływają  na  zachowanie 

systemu.
Jakikolwiek szeroki zbiór zmiennych stanu i zewnętrznych zaburzeń 

nie opisuje całkowicie wszystkich właściwości systemu. 

Dzieje się tak, ponieważ zachowanie rzeczywistego systemu zależy 

od  wielu  dodatkowych  czynników,  które  opisują  specyfikę  działania 

danego  systemu.  Różne  czynniki  takiego  rodzaju  nazywamy 

parametrami systemu

.

7

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Zbiór parametrów opisujących właściwości systemu można podzielić 

na dwie grupy:

parametry  techniczne

 –  określają    różnicę  pomiędzy 

poszczególnymi  systemami  działającymi  w  tych  samych 

warunkach,

parametry środowiska i warunków działania

 – określają różnice 

pomiędzy warunkami działania tego samego systemu.

Model dynamiczny

8

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Niech  będzie  dany  ciągły  system  dynamiczny,  w  którym  istnieją 

następujące zależności:

Model dynamiczny

Tak  zdefiniowany  system  dynamiczny  można  opisać  za  pomocą 

równania stanu

 – układu równań różniczkowych pierwszego rzędu:

Uzupełnieniem  opisu  są 

równania  wyjścia

 określające  związek 

między wielkościami wyjściowymi a zamiennymi stanu i wejścia:

X

t = X t

0

 ,U t ,t

0



Y

t = X t

0

 ,U t , t

0



˙X t=F

1

 X t

0

 ,U t , t

0



Y

t=F

2

 X t

0

 ,U t , t

0



9

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Najczęściej  stosowaną,  a  jednocześnie  najbardziej  ogólną  metodą 

formułowania  modeli  systemów  dynamicznych  opisanych  przy 

pomocy równań stanu i równań wyjście jest 

metoda bilansowa

.

W  systemach,  w  których  mamy  do  czynienia  z  wielkościami 

materialnymi,  bilansowaniu  najczęściej  podlegają  wielkości,  które 

podporządkowane  są 

zasadom  zachowania:  masy,  energii, 

ładunku, pędu i momentu pędu

.

W systemach ekonomiczno-społecznych odpowiednikiem energii czy 

masy  są  takie  wielkości  jak  zasoby  finansowe  lub  siła  robocza. 

Odpowiednikiem mocy są zdolności przerobowe lub zatrudnienie.

Model dynamiczny – formułowanie równań stanu

10

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – analogie między zjawiskami

Wielkość fizyczna

Elektrotechnika

DZIEDZINA

Termodynamika

Hydrodynamika

zbiornik

kondensator

ciało o jednolitej

temperaturze

zbiornik cieczy

kanał

przewodnik łączący dwa

kondensatory

powierzchnia styku dwóch

ciał

rurociąg między dwoma

zbiornikami

wielkość bilansowana q

ładunek elektryczny q

energia cieplna Q

masa m

natężenie przepływu

i = dq/dt 

natężenie prądu

elektrycznego  i = dq/dt

strumień ciepła  i = dQ/dt

strumień masy  i = dm/dt

potencjał 

φ

potencjał elektryczny 

φ

temperatura T

wysokość słupa cieczy h

11

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Etapy budowy modelu:

wybór wielkości bilansowych,

ułożenie równań bilansowych,

wybór wielkości stanu,

ułożenie równań stanu,

określenie wielkości wyjściowych.

 

Model dynamiczny – metoda bilansowa

12

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

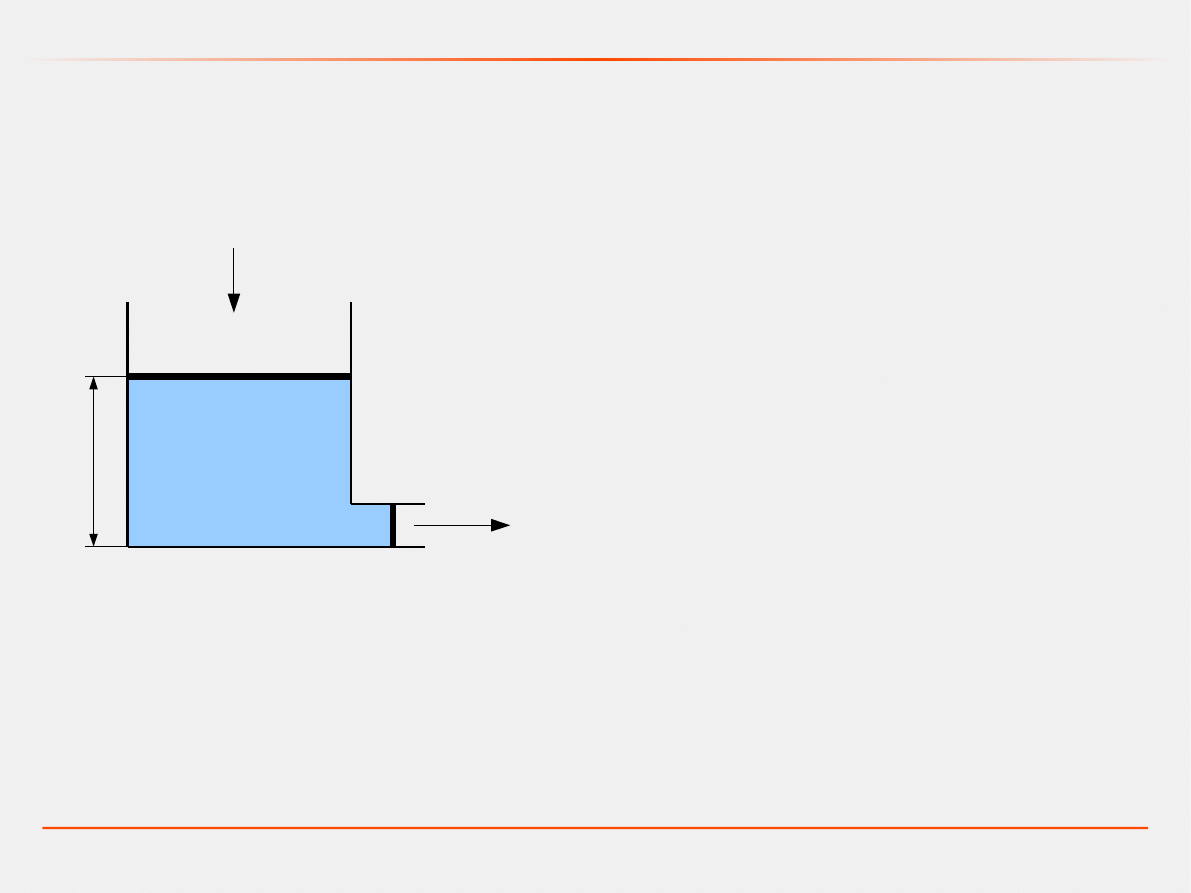
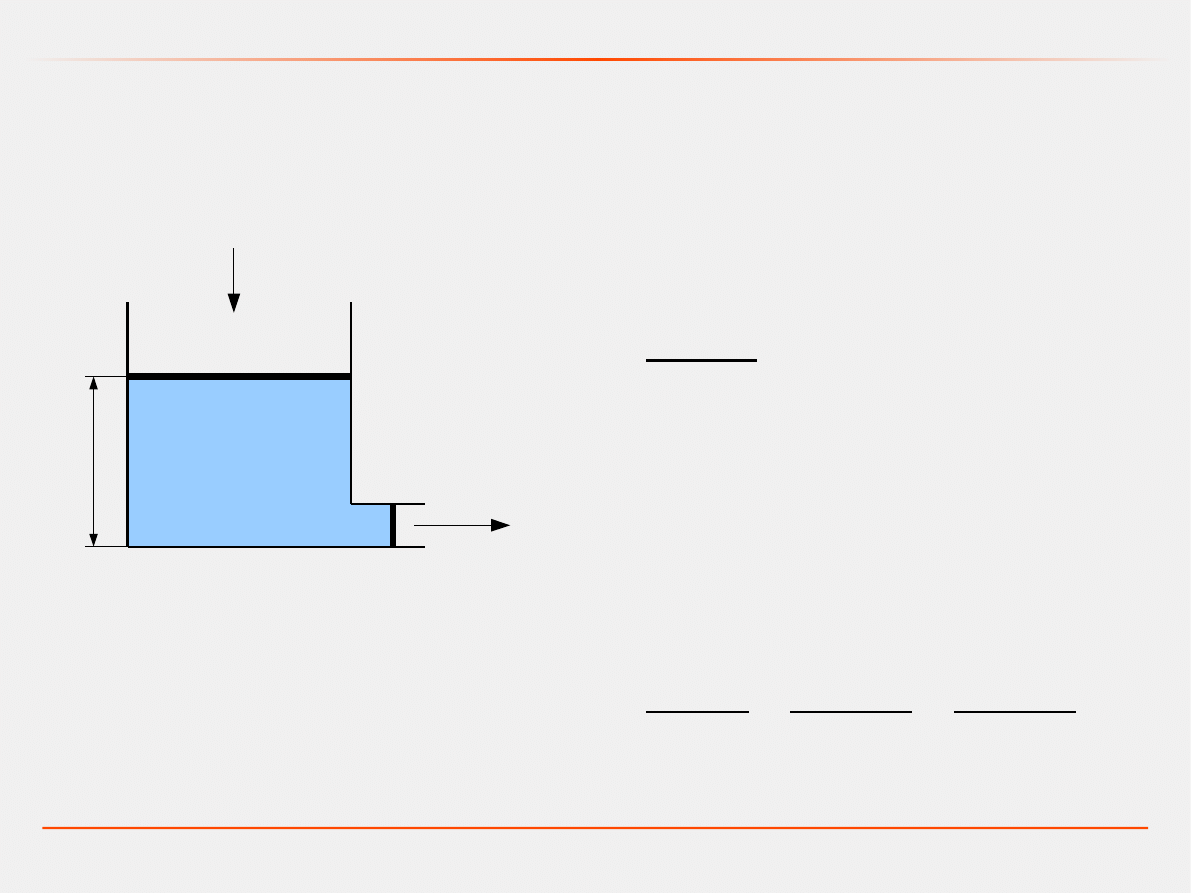
Przykład: Model zbiornika z cieczą

Model dynamiczny – metoda bilansowa

Q

we

Q

wy

h

S

wy

S

Q

we

(t)

 

– chwilowy dopływ,

Q

wy 

(t)– chwilowy odpływ,

S – przekrój poprzeczny zbiornika,
S

wy

 – przekrój poprzeczny odpływu,

h(t) – wysokość słupa cieczy,
w(t) – zapełnienie zbiornika (ilość cieczy)
 

w

13

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przykład: Model zbiornika z cieczą

Model dynamiczny – metoda bilansowa

Q

we

Q

wy

h

S

wy

S

w

Równanie bilansowe: 

Wielkość bilansowa:   

w(t)

dw

t 

dt

=Q

we

t−Q

wy

t 

w

t=S⋅ht

Zmienna stanu:   

h(t)

Równanie stanu: 

dh

t

dt

=

Q

we

t

S

−

Q

wy

t

S

14

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – metoda bilansowa

Prędkość wypływu 

v

wy

 cieczy doskonałej ze zbiornika przez mały otwór 

jest opisana równaniem: 

v

wy

=



2gh

t 

h(t)

 – wysokość słupa cieczy,

g

 – przyśpieszenie ziemskie,

Równanie na prędkość wypływu 

v

wy

 można wyprowadzić posługując się 

równaniem Bernoulliego dla przekrojów 

S

 i 

S

wy

:

v

we

2

2g



p

we

 g

h=

v

wy

2

2g



p

wy

 g

p

we

 – ciśnienie wejściowe,

p

wy

 – ciśnienie wyjściowe,

ρ

 – gęstość cieczy,

Z prawa ciągłości strugi wynika:

v

we

S

=v

wy

S

wy

15

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – metoda bilansowa

Po przekształceniach otrzymamy równanie na prędkość wypływu 

v

wy

 w 

postaci:

v

wy

=



2

[ gh− p

wy

− p

we

]



[

1

−



S

wy

S



2

]

Jeśli otwór wypływowy 

S

wy

 jest bardzo mały to:

1

−



S

wy

S



2

≃1

oraz 

p

we

 = 

p

wy

 = 

p

otoczenia

v

wy

=



2gh

t 

to otrzymamy:

16

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – metoda bilansowa

Ostatecznie wypływ określa zależność:

Q

wy

=S

wy

⋅v

wy

=S

wy

⋅



2gh

t 

Prędkość wypływu cieczy rzeczywistej jest zawsze mniejsza niż cieczy 

doskonałej.  Spowodowane  jest  to  siłami  tarcia  (lepkością),  a  także 

zwężeniem strumienia cieczy w pewnej odległości od otworu. Dla cieczy 

rzeczywistej można zatem zapisać:

v

wy

=



2gh

t 

Współczynnik

 

ϕ

 

nosi nazwę współczynnika wypływu. Jego wartość 

zależy od kształtu otworu wypływowego i jego usytuowania względem 
ścian zbiornika. Przybiera wartość 0 < 

ϕ

 < 1.

17

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

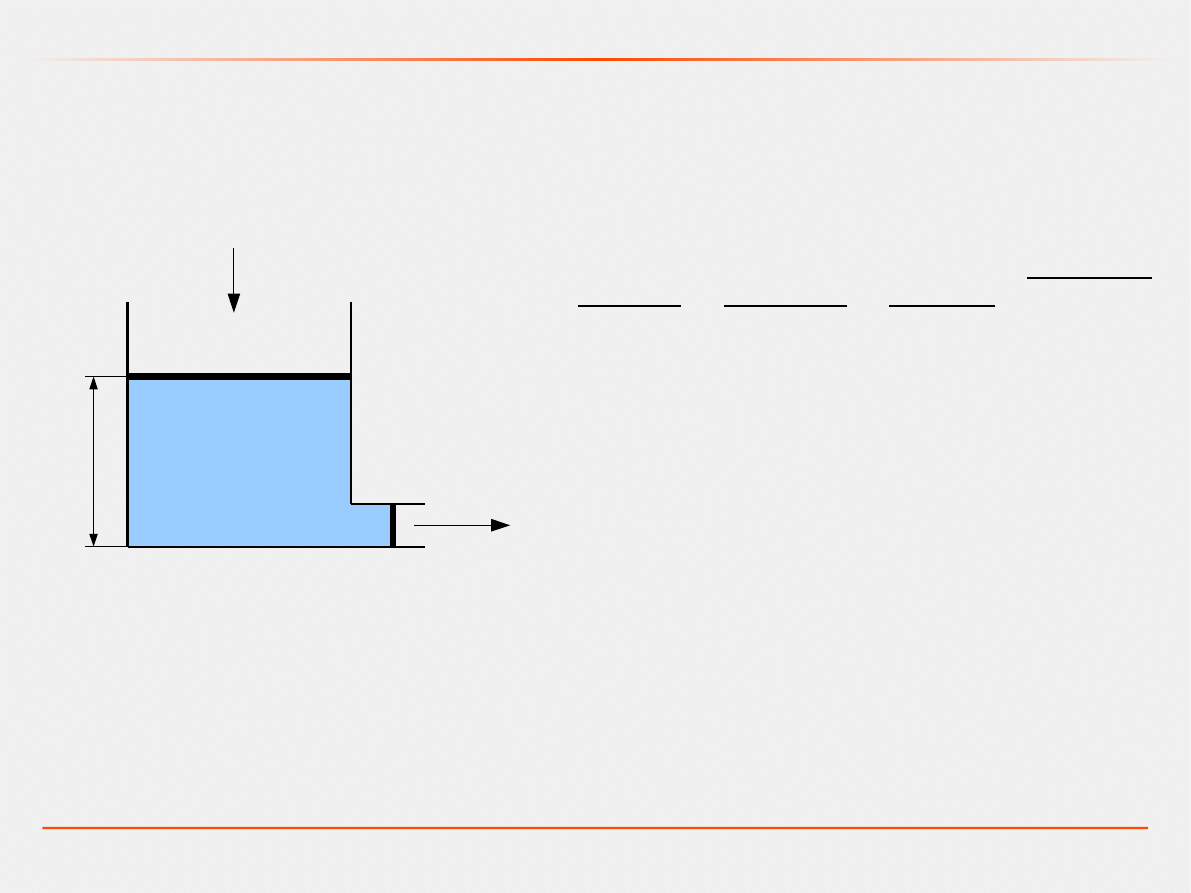
Przykład: Model zbiornika z cieczą

Model dynamiczny – metoda bilansowa

Q

we

Q

wy

h

S

wy

S

w

Równanie stanu: 

dh

t 

dt

=

Q

we

t

S

−

 S

wy

S



2gh

t 

Równanie wyjścia: 

y

t=ht

18

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Innymi  metodami  formułowania  modeli  systemów  dynamicznych 

opisanych  przy  pomocy  równań  stanu  są 

metody  wariacyjne

.  Ich 

podstawą  są  zasady  wariacyjne  mówiące,  że  ruch  układu 

dynamicznego  przebiega  tak,  aby  charakteryzujący  ten  układ 

funkcjonał czasowy, zwany działaniem, osiągnął wartość stacjonarną 

(zwykle  minimalną).  Najczęściej  wykorzystywana  jest 

zasada 

wariacyjna Hamiltona

 (

zasada najmniejszego działania

). 

Zasada  najmniejszego  działania  jest  najbardziej  ogólnym 

sformułowaniem  praw  ruchu  systemów  mechanicznych.  Dzięki 

zastosowaniu  odpowiednich  analogii  zasada  ta  pozwala  budować 

modele innych systemów (elektromechanicznych, elektrycznych)

Model dynamiczny – zasada najmniejszego działania

19

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Według  zasady  najmniejszego  działania  dla  każdego  systemu 
mechanicznego, w którym nie zachodzi rozpraszanie energii (system 
konserwatywny)  można  sformułować  funkcję  stanu  zwaną  funkcją 

Lagrange'a,           

spełniającą  warunek:  przebieg 

q

(t)

 od 

punktu  o  współrzędnych 

q

1

 do  punktu  o  współrzędnych 

q

2

 odbywa 

się w ten sposób, że całka określona w przedziale                           

z funkcji     

  :  

przyjmuje wartość minimalną. Wielkość 

S

 nazywa się działaniem.

Model dynamiczny – zasada najmniejszego działania

L

q , ˙q ,t

t

∈t

1

,t

2



L

q , ˙q ,t

S

=

∫

t

1

t

2

L

q , ˙q ,tdt

20

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Wyznaczenie funkcji 

q

(t), 

dla 

(t

1

, t

2

)

, która minimalizuje funkcjonał 

S

jest zadaniem rachunku wariacyjnego.

Po  dokonaniu  odpowiednich  przekształceń  matematycznych,  z 
zasady  najmniejszego  działania  uzyskujemy  model  dynamicznego 
systemu konserwatywnego w postaci równań Eulera-Lagrange'a

Model dynamiczny – zasada najmniejszego działania

d

dt



∂ L

∂ ˙q

k



− ∂

L

∂ q

k

=Q

k

k=1, N 

21

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Równania Eulera-Lagrange'a

Model dynamiczny – zasada najmniejszego działania

d

dt



∂ L

∂ ˙q

k



− ∂

L

∂ q

k

=Q

k

k=1, N 

N

 - liczba 

stopni swobody systemu 

–

 

równa liczbie współrzędnych 

uogólnionych (liczbie prędkości uogólnionych)

˙q

k

q

k

Q

k

- 

współrzędne 

uogólnione

, 

opisujące 

system 

po 

wyeliminowaniu zmiennych zależnych 

-  

prędkości uogólnione

.

-  

siła uogólniona 

związana ze współrzędną uogólnioną

q

k

-  

funkcja Lagrange'a

L

=Lq , ˙q ,t

22

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Równania Eulera-Lagrange'a

Model dynamiczny – zasada najmniejszego działania

d

dt



∂ L

∂ ˙q

k



− ∂

L

∂ q

k

=Q

k

k=1, N 

L

=T −U

Dla konserwatywnych systemów mechanicznych funkcja Lagrange'a 

jest  różnicą  między  energią  kinetyczną 

T

 a  energią  potencjalną 

U

systemu.

Ostatecznie równania Eulera-Lagrange'a przyjmie postać:

d

dt



∂T

∂ ˙q

k



− ∂

T

∂ q

k

 ∂

U

∂ q

k

=Q

k

NP

k=1, N 

23

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – zasada najmniejszego działania

Równania Eulera-Lagrange'a tworzą układ 

N

 równań różniczkowych 

zwyczajnych  rzędu  drugiego.  Równanie  te  uzupełnione  o 

2N

warunków  początkowych  jednoznacznie  określają  równania  ruchu 
konserwatywnego  systemu  mechanicznego.  Wyrażają  one  drugie 
prawo Newtona równowagi sił.